План решения задач с помощью законов динамики
1. Поступательное движение тел.
1) Выделите систему взаимодействующих тел. Сделайте рисунок.
2) Укажите на рисунке силы, действующие на каждое тело. Учтите, что силу трения можно показать, если известно направление движения.
3) Выберите систему координат. Удобно для каждого тела одну из координатных осей направить по направлению ускорения тела.
4) Запишите для каждого тела закон динамики движения – 2-й закон Ньютона, в следующем виде:
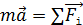 .
.
5) Запишите этот закон в проекциях на координатные оси и выразите определяемую величину.
6) По полученной расчетной формуле произведите вычисления.
2. Вращательное движение тел.
1) Запишите закон динамика вращательного движения тела относительно неподвижной оси вращения.
2) Покажите на рисунке плечо силы и расстояния масс от оси вращения, необходимые для расчета момента инерции тела. Запишите определительные формулы для момента силы M и момента инерции I; при этом обратите внимание на то, чтобы величины M и I , были записаны относительно одной и той же оси вращения тела.
3) Из закона динамики получите расчетную формулу определяемой величины и произведите вычисления.
Задача 4. Мяч массой 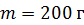 упруго ударяется о стену под углом
упруго ударяется о стену под углом 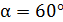 к нормали. Определите величину и направление импульса силы, который действовал на стенку во время удара. Скорость мяча
к нормали. Определите величину и направление импульса силы, который действовал на стенку во время удара. Скорость мяча 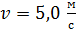 .
.
Дано Решение
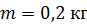 ; При упругом ударе величина скорости не изменяется
; При упругом ударе величина скорости не изменяется
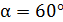 ; (
; ( 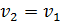 ) и угол, под которым отскакивает мяч, равен углу
) и угол, под которым отскакивает мяч, равен углу
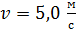 . падения мяча
. падения мяча 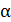 (рис. 4). Мяч в условии задачи можно
(рис. 4). Мяч в условии задачи можно
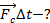 принять за материальную точку, пренебрегая его размерами,
принять за материальную точку, пренебрегая его размерами,
а стену рассматривать как абсолютно твердое тело.
При взаимодействии мяча со стеной на мяч действует Земля: силой тяжести, – и стена: силой упругости 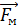 . Однако проекция силы тяжести на ось
. Однако проекция силы тяжести на ось 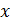 равна нулю; поэтому величину силы тяжести мяча можно исключить из дальнейшего рассмотрения. Под действием силы упругости
равна нулю; поэтому величину силы тяжести мяча можно исключить из дальнейшего рассмотрения. Под действием силы упругости 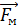 изменяется направление скорости мяча.
изменяется направление скорости мяча.
Запишем второй закон Ньютона в виде:
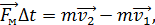 (1)
где (1)
где 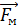 – средняя сила, с которой стена действует на мяч; – средняя сила, с которой стена действует на мяч; 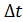 – время взаимодействия мяча со стеной. – время взаимодействия мяча со стеной.
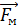 . Из уравнения (1) следует, что импульс силы удара мяча совпадает по направлению с вектором приращения импульса мяча . Из уравнения (1) следует, что импульс силы удара мяча совпадает по направлению с вектором приращения импульса мяча 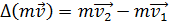 , т. е. , т. е. 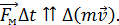
|
По правилу вычитания векторов
найдем вектор приращения импульса
мяча 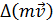
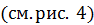 , он направлен
, он направлен
перпендикулярно поверхности стены.
Следовательно, и импульс силы 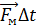 ,
,
действующий на мяч, направлен вдоль
нормали к поверхности стены.
Перепишем уравнение (1) в
проекции на ось x:
 .
.
Так как 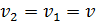 , то
, то
| Рис. 4 |
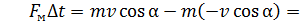
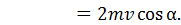 (2)
(2)
Нас интересует импульс силы, действующий на стену во время удара. Используем третий закон Ньютона: сила 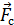 , с которой мяч действует на стену, равна по величине и противоположно направлена силе
, с которой мяч действует на стену, равна по величине и противоположно направлена силе 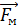 , с которой стена действует на мяч (см. рис. 4):
, с которой стена действует на мяч (см. рис. 4):
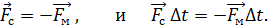
Отсюда, с учетом формулы (2), получаем 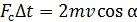 .
.
Вычислим импульс силы: 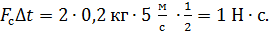
Задача 5. Маховик в виде диска радиусом 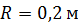 и массой
и массой 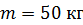 был раскручен до частоты вращения
был раскручен до частоты вращения 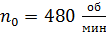 , а затем был предоставлен самому себе. Под действием сил трения маховик остановился через
, а затем был предоставлен самому себе. Под действием сил трения маховик остановился через 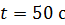 . Определите момент сил трения.
. Определите момент сил трения.
Дано Решение
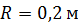 ; В соответствии с основным законом динамики
; В соответствии с основным законом динамики
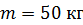 ; вращательного движения момент сил трения равен
; вращательного движения момент сил трения равен
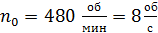 ; скорости изменения момента импульса маховика:
; скорости изменения момента импульса маховика:
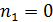 ;
; 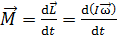 . (1)
. (1)
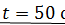 . По условию задачи маховик представляет собой
. По условию задачи маховик представляет собой 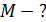 твердый сплошной диск, момент инерции которого
твердый сплошной диск, момент инерции которого
относительно его оси симметрии
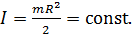 (2)
(2)
С учетом формулы (2) из закона динамики (1) получаем момент сил трения
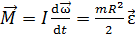 , (3)
, (3)
где 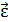 – угловое ускорение маховика.
– угловое ускорение маховика.
Так как угловое ускорение 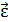 и момент сил трения в данном случае сонаправлены, то векторное уравнение (3) можно заменить скалярным:
и момент сил трения в данном случае сонаправлены, то векторное уравнение (3) можно заменить скалярным:
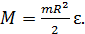 (4)
(4)
При равнозамедленном вращении (вектор 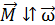 (рис. 5)) величина углового ускорения определяется выражением
(рис. 5)) величина углового ускорения определяется выражением
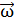
|
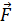
|
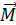
|
| Рис. 5 |
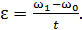 (5)
(5)
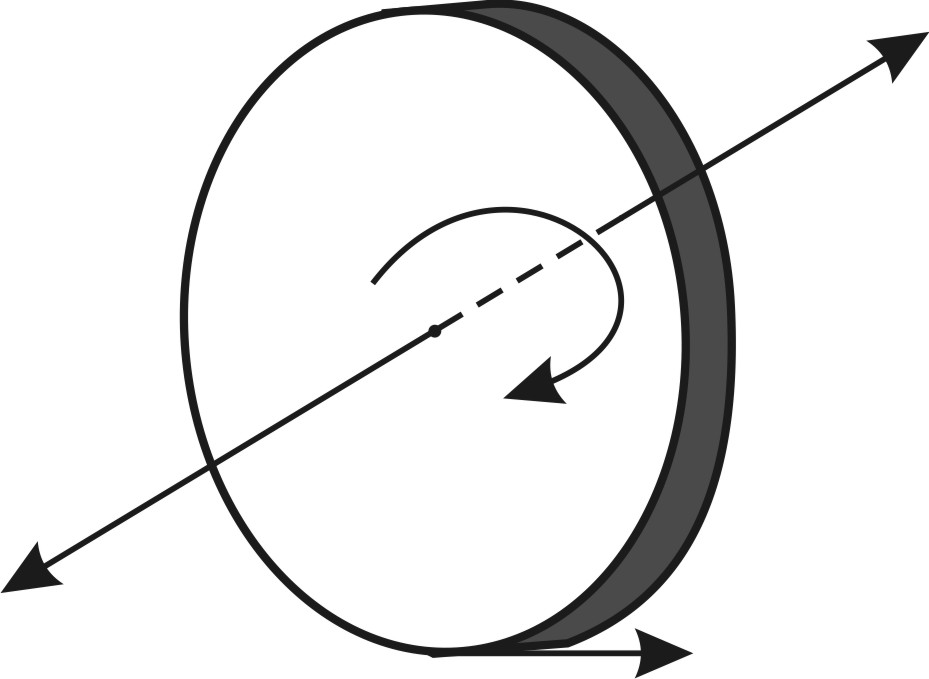 Здесь конечная угловая скорость
Здесь конечная угловая скорость 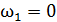 , а начальная
, а начальная 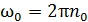 . Подставив ускорение
. Подставив ускорение 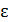 в закон динамики (4), получаем величину момента силы
в закон динамики (4), получаем величину момента силы
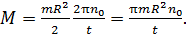 (6)
(6)
Проверим расчетную формулу (6) по единицам измерения. Подстановка единиц измерения величин в правую часть этого равенства:
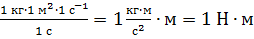 , –
, –
дает единицу определяемой физической величины – момента сил.
Вычисляем момент силы трения по формуле (6):
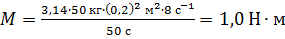 .
.
| Рис. 6 |
|
|
|
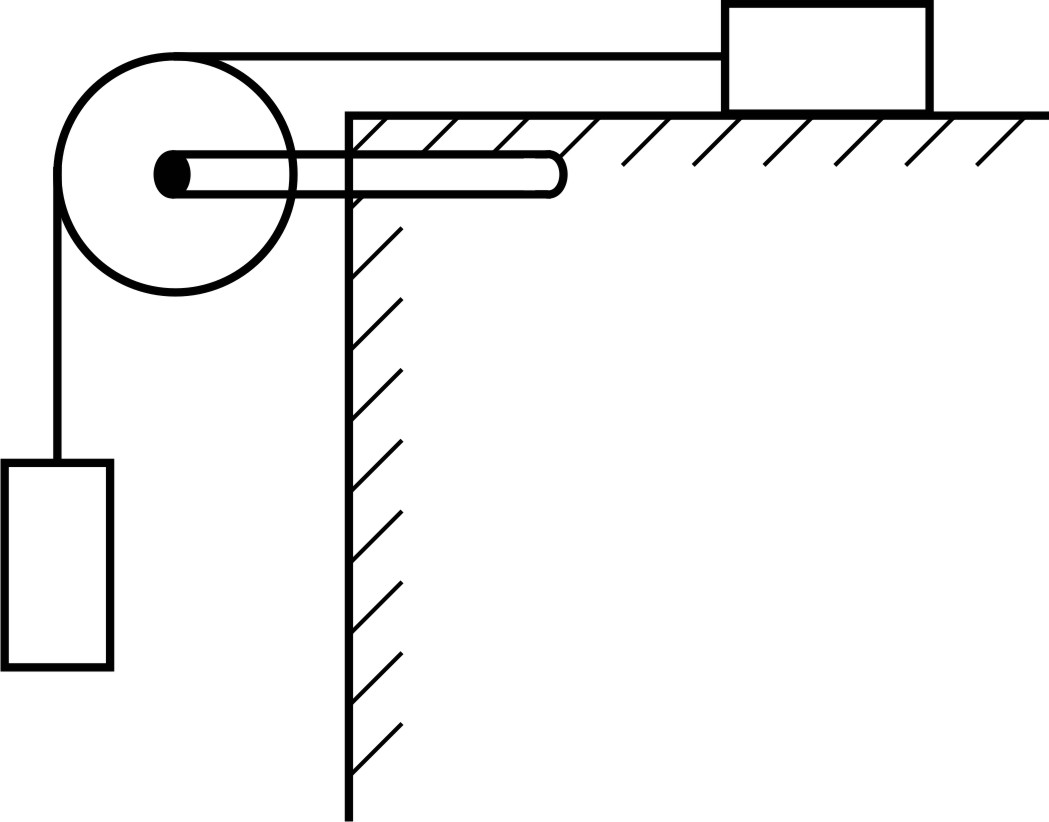 Задача 6. Блок, имеющий форму диска массой
Задача 6. Блок, имеющий форму диска массой 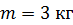 , укреплен на краю горизонтального стола. Гири массой
, укреплен на краю горизонтального стола. Гири массой 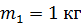 и
и 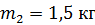 соединены невесомой нитью, перекинутой через блок (рис. 6). Коэффициент трения гири о поверхность стола
соединены невесомой нитью, перекинутой через блок (рис. 6). Коэффициент трения гири о поверхность стола 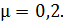 Определите ускорение
Определите ускорение 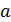 , с которым движутся гири, и силы натяжения нити
, с которым движутся гири, и силы натяжения нити 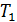 и
и 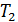 по обе стороны блока. Трением при вращении блока можно пренебречь.
по обе стороны блока. Трением при вращении блока можно пренебречь.
Решение
Механическая система состоит из трех тел, взаимодействующих посредством нити. В таких случаях рассматривают отдельно движение каждого тела, мысленно разрывая нить и заменяя действие других тел на данное силой натяжения нити. Силы, действующие на каждое тело, показаны на рис. 7. При этом следует учесть, что для сил взаимодействия двух тел выполняется третий закон Ньютона:
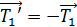 ;
; 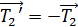 ; модули сил
; модули сил 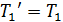 ;
; 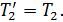 (1)
(1)
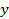
|
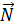
|
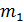
|
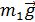
|
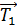
|
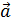
|
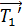
|
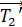
|
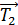
|
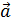
|
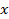
|
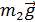
|
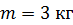 ; ;
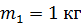 ; ;
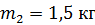 ; ;
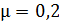 . .
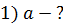
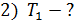
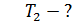
| 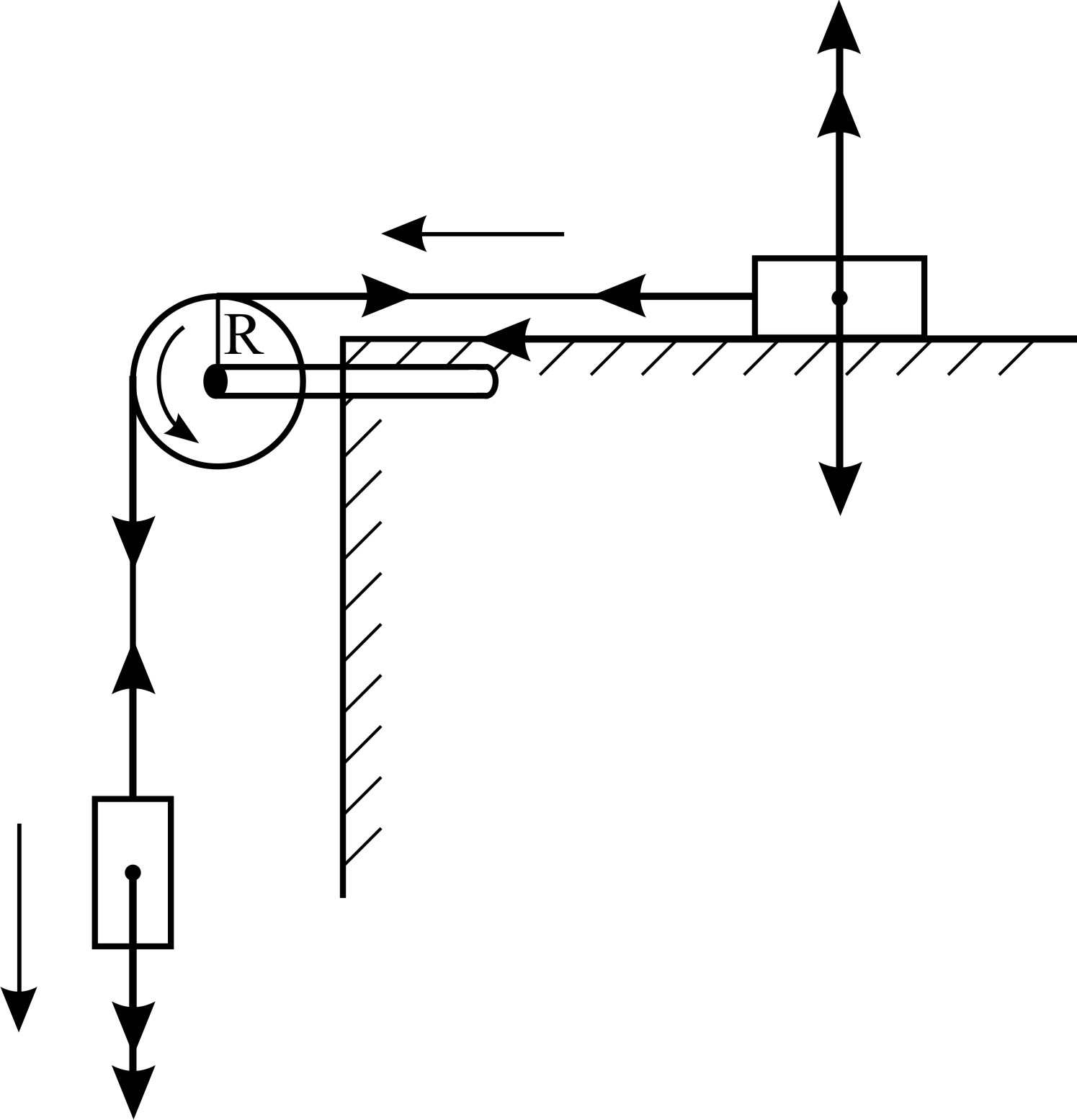 Рис. 7
Рис. 7
|
Запишем законы динамики движения тел системы, учитывая, что гири движутся поступательно, а блок вращается. Для поступательного движения тел используем второй закон Ньютона:
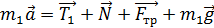 ; (2)
; (2)
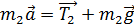 . (3)
. (3)
ось x: 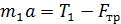 ; (4)
; (4)
ось y: 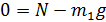 . (5)
. (5)
В уравнении (4) сила трения 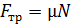 ; заменяя, согласно уравнению (5),
; заменяя, согласно уравнению (5), 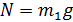 , получаем формулу
, получаем формулу 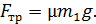 С учетом этого перепишем уравнение (4) в виде:
С учетом этого перепишем уравнение (4) в виде:
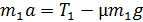 . (6)
. (6)
Уравнение (3) запишем в проекции на ось x, направленную вдоль ускорения второй гири:
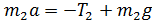 . (7)
. (7)
Закон динамики вращения блока относительно неподвижной оси z имеет следующий вид:
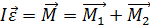 , (8)
, (8)
где 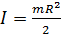 – момент инерции блока (диска) относительно его оси симметрии;
– момент инерции блока (диска) относительно его оси симметрии; 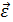 – угловое ускорение блока; оно связано с линейным ускорением точек на его периметре формулой
– угловое ускорение блока; оно связано с линейным ускорением точек на его периметре формулой 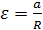 , причем, величина
, причем, величина 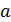 равна ускорению нити, не проскальзывающей по блоку, а следовательно, и ускорению гирь;
равна ускорению нити, не проскальзывающей по блоку, а следовательно, и ускорению гирь; 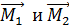 – моменты сил натяжения нити
– моменты сил натяжения нити 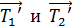 .
.
Из рисунка (см. рис. 7) видно, что момент силы 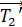 вращает блок против часовой стрелки, а момент силы
вращает блок против часовой стрелки, а момент силы 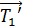 препятствует этому вращению, стремясь повернуть блок по часовой стрелке. Соответственно вектор
препятствует этому вращению, стремясь повернуть блок по часовой стрелке. Соответственно вектор 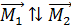 , – они направлены по оси вращения z, перпендикулярной плоскости рисунка. Поэтому модуль равнодействующего момента сил
, – они направлены по оси вращения z, перпендикулярной плоскости рисунка. Поэтому модуль равнодействующего момента сил
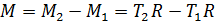 . (9)
. (9)
Здесь учтено, что плечо обеих сил натяжения нити равно радиусу диска R.
С использованием формул для 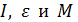 уравнение (8) принимает следующий вид:
уравнение (8) принимает следующий вид:
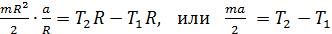 . (10)
. (10)
Таким образом, получили систему трех уравнений законов динамики движения тел (6), (7) и (10), позволяющих найти 3 неизвестные величины ( 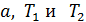 ) в виде:
) в виде:
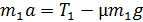 ;
;
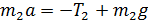 ; (11)
; (11)
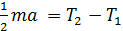 ;
;
Заметим, что при сложении уравнений системы (11) неизвестные величины 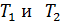 исключаются (сумма этих слагаемых равна нулю) и получаем уравнение с одной неизвестной величиной
исключаются (сумма этих слагаемых равна нулю) и получаем уравнение с одной неизвестной величиной 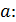
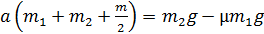 .
.
Выразим определяемую величину ускорения гирь:
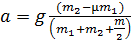 .
.
Вычисляем 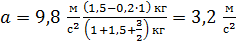 .
.
Силу натяжения нити 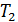 выразим из закона динамики (7):
выразим из закона динамики (7):
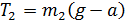 ,
,
а силу натяжения нити 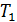 – из закона динамики вращения блока (третье уравнение в системе уравнений (11)):
– из закона динамики вращения блока (третье уравнение в системе уравнений (11)):
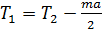 .
.
Вычисляем силы натяжения:
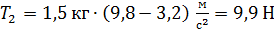 ;
;  .
.
Задача 7. На обод маховика радиусом 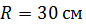 намотан нерастяжимый шнур, к концу которого привязан груз массой
намотан нерастяжимый шнур, к концу которого привязан груз массой 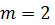 кг. Определите момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время
кг. Определите момент инерции маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время 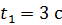 приобрел угловую скорость
приобрел угловую скорость 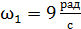 .
.
Дано Решение
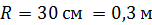 ; ;
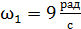 . .
|
Составим систему уравнений движения двух связанных шнуром тел (рис. 8), одно из которых: груз, – совершает поступательное движение, а другое: маховик, – вращательное.
Запишем закон динамики движения груза – второй закон Ньютона: 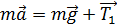 .
.
В проекции на ось 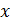
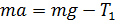 . (1)
. (1)
Основной закон динамики вращательного движения маховика
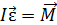 .
.
Так как векторы 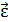 и
и 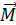 сонаправлены, то в скалярном виде
сонаправлены, то в скалярном виде
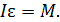 (2)
(2)
Из закона динамики (2) выразим определяемую величину момента инерции маховика:
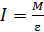 . (3)
. (3)
Угловое ускорение 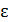 для равноускоренного движения маховика
для равноускоренного движения маховика
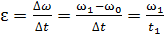 . (4)
. (4)
Момент силы натяжения шнура
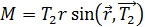 .
.
Так как угол между радиус-вектором 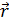 , проведенным от оси вращения в точку приложения силы натяжения шнура, и силой натяжения равен 900 (см. рис. 8), а численное значение радиус-вектора равно радиусу маховика R, то для момента силы натяжения получаем следующее выражение:
, проведенным от оси вращения в точку приложения силы натяжения шнура, и силой натяжения равен 900 (см. рис. 8), а численное значение радиус-вектора равно радиусу маховика R, то для момента силы натяжения получаем следующее выражение:
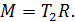
Силу натяжения шнура найдем, используя закон движения груза (1). По третьему закону Ньютона для взаимодействия груза и маховика посредством шнура силы натяжения численно равны: 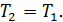 Тогда формула для момента силы, вращающей маховик, принимает вид:
Тогда формула для момента силы, вращающей маховик, принимает вид:
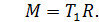 (5)
(5)
Значение 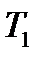 находим из уравнения движения груза (1):
находим из уравнения движения груза (1):
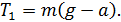 (6)
(6)
Здесь ускорение груза a равно ускорению любой точки нерастяжимого шнура, в том числе и точки, находящейся на ободе маховика, для которой запишем связь линейного и углового ускорения в виде:
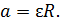 (7)
(7)
С учетом выражений (6) и (7) формула (5) для момента силы принимает следующий вид:
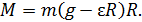 (8)
(8)
Подставим выражение (8) в формулу (3) для расчета момента инерции и заменим угловое ускорение по формуле (4). Так получаем расчетную формулу для определения момента инерции маховика динамическим методом:
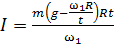 , или
, или 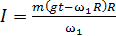 .
.
Проверим полученную формулу по единицам измерения величин:
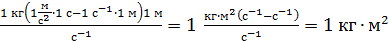 .
.
Получили единицу измерения момента инерции I, следовательно, расчетная формула верна. Вычисляем по ней момент инерции маховика
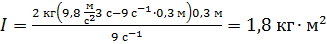 .
.
Задача 8. Какой кинетической энергией обладает велосипедист с велосипедом при скорости движения 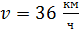 ? Масса велосипедиста вместе с велосипедом
? Масса велосипедиста вместе с велосипедом 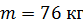 , в том числе масса каждого колеса велосипеда
, в том числе масса каждого колеса велосипеда 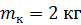 ; массу колеса считать распределенной по ободу.
; массу колеса считать распределенной по ободу.
Дано
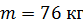 ; ;
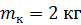 ; ;
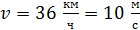 . .
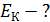
| Решение Кинетическая энергия велосипедиста вместе с велосипедом складывается из двух слагаемых: энергии их поступательного движения и энергии вращательного движения колес. Колеса участвуют одновременно в этих двух видах движения. Кинетическая энергия поступательного движения |
равна 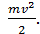 Кинетическая энергия вращательного движения колеса равна
Кинетическая энергия вращательного движения колеса равна 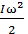 , где I – момент инерции колеса. Он равен
, где I – момент инерции колеса. Он равен 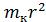 , так как массу считаем распределенной по ободу радиусом
, так как массу считаем распределенной по ободу радиусом 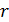 . С учетом того, что угловая скорость вращения связана с линейной скоростью формулой
. С учетом того, что угловая скорость вращения связана с линейной скоростью формулой 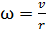 , кинетическую энергию вращательного движения колеса можно записать через скорость поступательного движения:
, кинетическую энергию вращательного движения колеса можно записать через скорость поступательного движения:
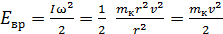 .
.
Тогда полная кинетическая энергия велосипедиста с велосипедом
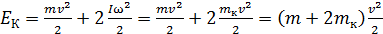 .
.
Найдем численное значение кинетической энергии:
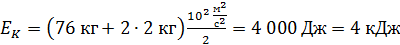 .
.
Законы сохранения
План решения задач с использованием законов сохранения:
ЗСИ, ЗСМИ и ЗСМЭ
Динамические функции механической системы: импульс, момент импульса, механическая энергия, – сохраняются при выполнении определенных условий. Поэтому выбору того или иного закона сохранения, например, при вращательном движении – ЗСМИ или ЗСМЭ, должен предшествовать анализ сил, действующих между телами механической системы.
1. Для сохранения количества движения: импульса или момента импульса, – требуется замкнутая система тел, т. е. отсутствие внешних сил или равенство нулю равнодействующей всех внешних сил. Но в ряде задач, к которым относятся удары шаров, разрыв гранаты, снаряда и др., достаточно, чтобы внутренние силы были большими по сравнению с внешними силами, тогда последними можно пренебречь и считать систему практически замкнутой. Для сохранения момента импульса достаточным является условие равенства нулю момента внешних сил, что обеспечивается, если силы параллельны оси вращения или когда линия их действия проходит через ось вращения.
2. Использование закона сохранения механической энергии возможно, если в рассматриваемой системе тел действуют только консервативные силы – и внутренние, и внешние. При этом силы трения и сопротивления движению и другие неконсервативные силы (работу которых невозможно представить как изменение потенциальной энергии), должны быть пренебрежимо малы по сравнению с консервативными силами. Однако, и при значительной величине силы трения возможно сохранение механической энергии, если работа силы трения равна нулю: для этого достаточно, чтобы не перемещалась точка приложения силы трения (или другой неконсервативной силы).
3. Способ решения задач с использованием того или иного закона сохранения заключается в составлении равенства, где значения сохраняющейся величины: импульса, момента импульса или механической энергии системы тел, – записывают в левой и в правой части, соответственно, в двух состояниях: начальном и конечном. Причем, для векторных величин импульса 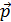 и момента импульса
и момента импульса 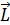 уравнения законов сохранения – векторные.
уравнения законов сохранения – векторные.
4. В связи с тем, что скорости тел: и линейная, и угловая, – величины относительные, то и связанные с ними динамические функции: импульс, момент импульса и кинетическая энергия тел, – также являются относительными величинами, т. е. их значения зависят от выбранной системы отсчета. Поэтому в уравнения законов сохранения следует записывать скорости тел относительно одной и той же системы отсчета: обычно используют условно неподвижную систему отсчета, связанную с Землей.
Задача 9. Молот массой 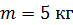 , двигаясь со скоростью
, двигаясь со скоростью 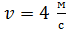 , ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием
, ударяет по железному изделию, лежащему на наковальне. Масса наковальни вместе с изделием 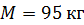 . Считая удар неупругим, определите энергию, расходуемую на ковку (деформацию) изделия. Найдите коэффициент полезного действия
. Считая удар неупругим, определите энергию, расходуемую на ковку (деформацию) изделия. Найдите коэффициент полезного действия 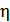 процесса ковки в данных условиях.
процесса ковки в данных условиях.
Дано Решение
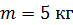 ; Рассмотрим систему молот – наковальня – Земля (рис. 9).
; Рассмотрим систему молот – наковальня – Земля (рис. 9).
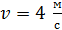 ; Эта система является замкнутой, так как силы, возникающие
; Эта система является замкнутой, так как силы, возникающие
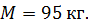 при взаимодействии тел системы: сила тяжести, сила
при взаимодействии тел системы: сила тяжести, сила
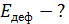 реакции опоры, на которой стоит наковальня, силы
реакции опоры, на которой стоит наковальня, силы
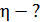 неупругой деформации (подобные силам трения), – являются
неупругой деформации (подобные силам трения), – являются
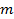 m m
|
| M |
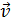
|
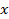
|
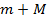
|
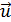
|
| Рис. 9 |
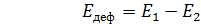 .
.
Незначительным перемещением
изделия и наковальни можно пренебречь, поэтому изменение потенциальной энергии 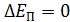 . Изменением механической энергии Земли в результате взаимодействия также можно пренебречь. Это означает, что на деформацию идет только часть кинетической энергии:
. Изменением механической энергии Земли в результате взаимодействия также можно пренебречь. Это означает, что на деформацию идет только часть кинетической энергии:
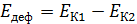 , (1)
, (1)
где 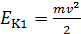 – кинетическая энергия молота перед ударом;
– кинетическая энергия молота перед ударом;
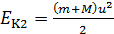 – энергия молота и наковальни с изделием после неупругого удара.
– энергия молота и наковальни с изделием после неупругого удара.
Скорость системы 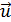 после неупругого удара определим из закона сохранения импульса:
после неупругого удара определим из закона сохранения импульса:
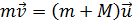 , (2)
, (2)
где 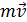 – импульс системы до удара;
– импульс системы до удара; 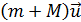 – импульс после удара.
– импульс после удара.
Проекция уравнения ЗСИ (2) на ось x:
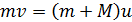 ;
; 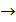
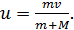 (3)
(3)
Энергию деформации найдем по уравнению (1) с учетом формулы (3):
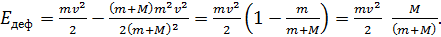 (4)
(4)
Подставим значения величин в расчетную формулу (4):
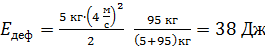 .
.
Эта энергия деформации по условию задачи является полезной, а затраченной энергией является первоначальная энергия молота перед ударом
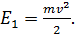 (5)
(5)
Следовательно, коэффициент полезного действия процесса ковки
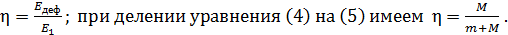 (6)
(6)
Вычислим КПД процесса ковки 
Задача 10. Шар массой 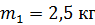 , движущийся со скоростью
, движущийся со скоростью 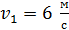 , сталкивается с шаром массой
, сталкивается с шаром массой 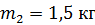 , который движется ему навстречу со скоростью
, который движется ему навстречу со скоростью 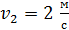 . Определите: а) скорость шаров после удара, б) кинетическую энергию шаров до и после удара, в) энергию, затраченную на деформацию шаров при ударе. Удар считайте прямым, неупругим, центральным.
. Определите: а) скорость шаров после удара, б) кинетическую энергию шаров до и после удара, в) энергию, затраченную на деформацию шаров при ударе. Удар считайте прямым, неупругим, центральным.
Дано Решение
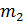
|
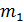
|
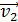
|
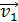
|
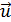
|
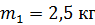 ;
;

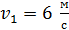 ;
;
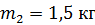 ;
;
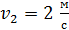 .
.
| Рис. 10 |
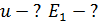
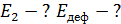
а) Неупругие шары после удара не восстанавливают свою форму (рис. 10). Следовательно, не возникают силы, способные оттолкнуть шары друг от друга. Это приводит к тому, что шары после удара движутся вместе со скоростью 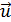 . Определим эту скорость, используя закон сохранения импульса. Шары образуют замкнутую систему и поэтому, согласно ЗСИ:
. Определим эту скорость, используя закон сохранения импульса. Шары образуют замкнутую систему и поэтому, согласно ЗСИ:
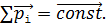
До удара суммарный импульс двух шаров
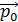
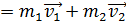 .
.
После взаимодействия их суммарный импульс
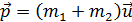 .
.
Следовательно, уравнение ЗСИ имеет следующий вид:
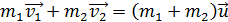 , (1)
, (1)
Запишем проекцию уравнения (1) на ось 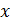 :
:
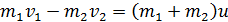 ,
,
выразим скорость шаров после удара и вычислим её:
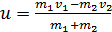
 .
.
б) Кинетическую энергию шаров до и после удара определим по формулам:
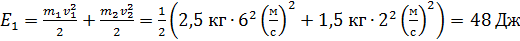 ;
;
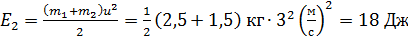 .
.
в) Энергия деформации равна разности кинетических энергий шаров до и после удара:
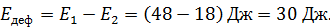
Можно также вычислить долю энергии, пошедшей на деформацию:
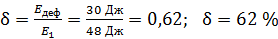 .
.
Задача 11. Шар массой 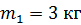 , движущийся горизонтально со скоростью
, движущийся горизонтально со скоростью 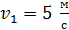 , столкнулся с неподвижным шаром массой
, столкнулся с неподвижным шаром массой 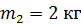 . Шары упругие, удар центральный. Определите: а) скорости шаров после удара, б) долю d кинетической энергии, которую первый шар передал второму.
. Шары упругие, удар центральный. Определите: а) скорости шаров после удара, б) долю d кинетической энергии, которую первый шар передал второму.
Дано Решение
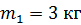 ; а) Соударяющиеся шары (рис. 11) образуют замкнутую
; а) Соударяющиеся шары (рис. 11) образуют замкнутую
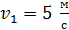 ; консервативную систему. Из этого следует, что при их
; консервативную систему. Из этого следует, что при их
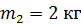 ; взаимодействии выполняется и закон сохранения импульса
; взаимодействии выполняется и закон сохранения импульса
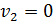 .
. 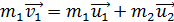 , (1)
, (1)
и закон сохранения механической энергии
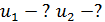
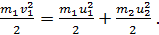 (2)
(2)
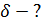
| до удара |
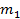
|
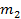
|
| после удара |
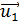
|
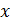
|
| Рис.11 |
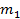
|
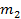
|
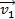
|
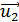
|
Для центрального удара можно от векторной записи ЗСИ (1) перейти к записи его в проекции на ось х:
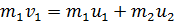 . (3)
. (3)
Для решения нелинейной системы уравнений (2) и (3) получим линейное уравнение путем деления равенства (2) на (3). Чтобы массы шаров сократились при делении, перенесем в левую часть каждого уравнения слагаемое, содержащее 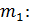
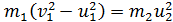 ; (2a)
; (2a)
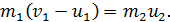 (3a)
(3a)
Разделим уравнение (2а) на (3а), при этом получим линейное уравнение
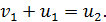 (4)
(4)
Далее решаем систему двух линейных уравнений: (3) и (4). Из уравнения (4) выразим скорость 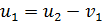 и подставим ее в уравнение (3):
и подставим ее в уравнение (3):
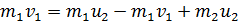 ;
; 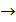
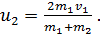 (5)
(5)
Из уравнения (4) найдем скорость 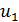 , используя полученную величину
, используя полученную величину 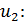
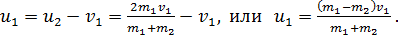 (6)
(6)
Вычисляем скорости шаров после удара по формулам (5) и (6):
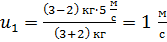 .
. 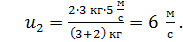
б) Доля энергии 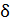 , переданной первым шаром второму, выразится отношением
, переданной первым шаром второму, выразится отношением
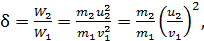 (7)
(7)
где 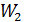 – кинетическая энергия второго шара после удара,
– кинетическая энергия второго шара после удара, 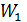 – кинетическая энергия первого шара до удара,
– кинетическая энергия первого шара до удара,
Подставляя в соотношение (7) величину 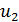 по формуле (5), имеем:
по формуле (5), имеем:
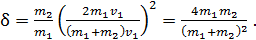 (8)
(8)
Из полученного выражения видно, что доля переданной энергии зависит только от масс сталкивающихся шаров и не зависит от их скоростей. Вычислим долю 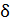 переданной энергии по формуле (8):
переданной энергии по формуле (8):
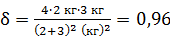 ;
; 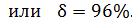
Задача 12. Пуля массой 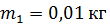 попадает в деревянный брусок массой
попадает в деревянный брусок массой 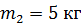 , подвешенный на нити, и застревает в нем. Определите скорость пули, если брусок вместе с пулей, отклонившись от первоначального положения, поднимается на высоту
, подвешенный на нити, и застревает в нем. Определите скорость пули, если брусок вместе с пулей, отклонившись от первоначального положения, поднимается на высоту 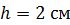 .
.
Дано Решение
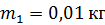 ; Рассмотрим систему пуля – брусок– Земля. Выясним
; Рассмотрим систему пуля – брусок– Земля. Выясним
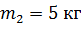 ; характер взаимодействия тел в различных положениях
; характер взаимодействия тел в различных положениях 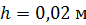 . бруска. Систему отсчета свяжем с Землей. В момент
. бруска. Систему отсчета свяжем с Землей. В момент 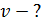 неупругого удара в системе действуют внутренние силы: сила тяжести
неупругого удара в системе действуют внутренние силы: сила тяжести 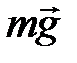 , сила упругой реакции нити, а также силы неупругой деформации, аналогичные силам трения. Следовательно, в момент удара в системе не выполняется закон сохранения механической энергии. А закон сохранения импульса выполняется, так как система замкнута. После взаимодействия пули с бруском: между положениями 1 и 2 (рис. 10), – действие силы неупругой деформации исчезает, а работу совершает только консервативная сила тяжести; значит, можно использовать закон сохранения механической энергии.
, сила упругой реакции нити, а также силы неупругой деформации, аналогичные силам трения. Следовательно, в момент удара в системе не выполняется закон сохранения механической энергии. А закон сохранения импульса выполняется, так как система замкнута. После взаимодействия пули с бруском: между положениями 1 и 2 (рис. 10), – действие силы неупругой деформации исчезает, а работу совершает только консервативная сила тяжести; значит, можно использовать закон сохранения механической энергии.
Проведенный анализ позволяет для абсолютно неупругого удара пули и бруска записать закон сохранения импульса в виде:
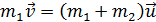 .
.
Здесь в левой части записан импульс системы до взаимодействия пули с бруском, равный импульсу пули, а справа – импульс бруска с пулей после их соударения. Запишем ЗСИ в проекции на ось 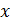 : :
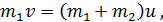
и выразим скорость бруска с пулей:
|
|
Следовательно, брусок с пулей в положении 1 после неупругого удара обладает кинетической энергией
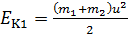 .
.
Потенциальная энергия бруска в этом положении 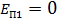 , так как приняли
, так как приняли 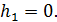 За счет кинетической энергии брусок отклонится от положения равновесия и поднимется на высоту h, в положение 2. В этом положении скорость бруска и его кинетическая энергия равна нулю:
За счет кинетической энергии брусок отклонится от положения равновесия и поднимется на высоту h, в положение 2. В этом положении скорость бруска и его кинетическая энергия равна нулю: 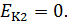
При переходе системы пуля – брусок – Земля из положения 1 в 2, для системы выполняется закон сохранения механической энергии:
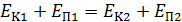 , (2)
, (2)
где 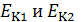 – кинетическая энергия системы в положениях 1 и 2;
– кинетическая энергия системы в положениях 1 и 2; 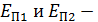 потенциальная энергия системы в этих положениях. Подставим величины энергий в формулу ЗСМЭ (2):
потенциальная энергия системы в этих положениях. Подставим величины энергий в формулу ЗСМЭ (2):
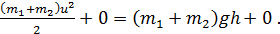 (3)
(3)
Из этого уравнения видно, что кинетическая энергия бруска в положении 1 полностью переходит в его потенциальную энергию в положении 2. Согласно уравнению (3)
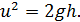 (4)
(4)
Подставим в это уравнение скорость бруска u по формуле (1):
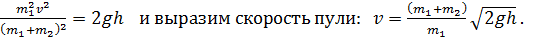 (5)
(5)
Упростим формулу (5): с учетом того, что масса пули 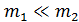 , величиной
, величиной 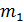 , как слагаемым, можно пренебречь, – тогда определяемая скорость пули
, как слагаемым, можно пренебречь, – тогда определяемая скорость пули
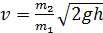 .
.
Вычислим величину 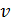 :
:
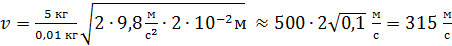 .
.
Задача 13. Диск радиусом 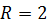 см начинает скатываться с высоты
см начинает скатываться с высоты 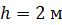 по наклонной плоскости, образующей угол
по наклонной плоскости, образующей угол 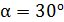 с плоскостью горизонта
с плоскостью горизонта  С каким ускорением движется центр масс диска? Найдите линейную скорость центра масс в конце наклонной плоскости.
С каким ускорением движется центр масс диска? Найдите линейную скорость центра масс в конце наклонной плоскости.
Дано Решение
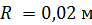 ; Есть два пути решения данной задачи: с помощью
; Есть два пути решения данной задачи: с помощью
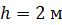 ; законов динамики поступательного и вращательного
; законов динамики поступательного и вращательного
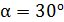 . движения и с использованием закона сохранения
. движения и с использованием закона сохранения
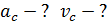 механической энергии (ЗСМЭ).
механической энергии (ЗСМЭ).
1-й путь решения задачи
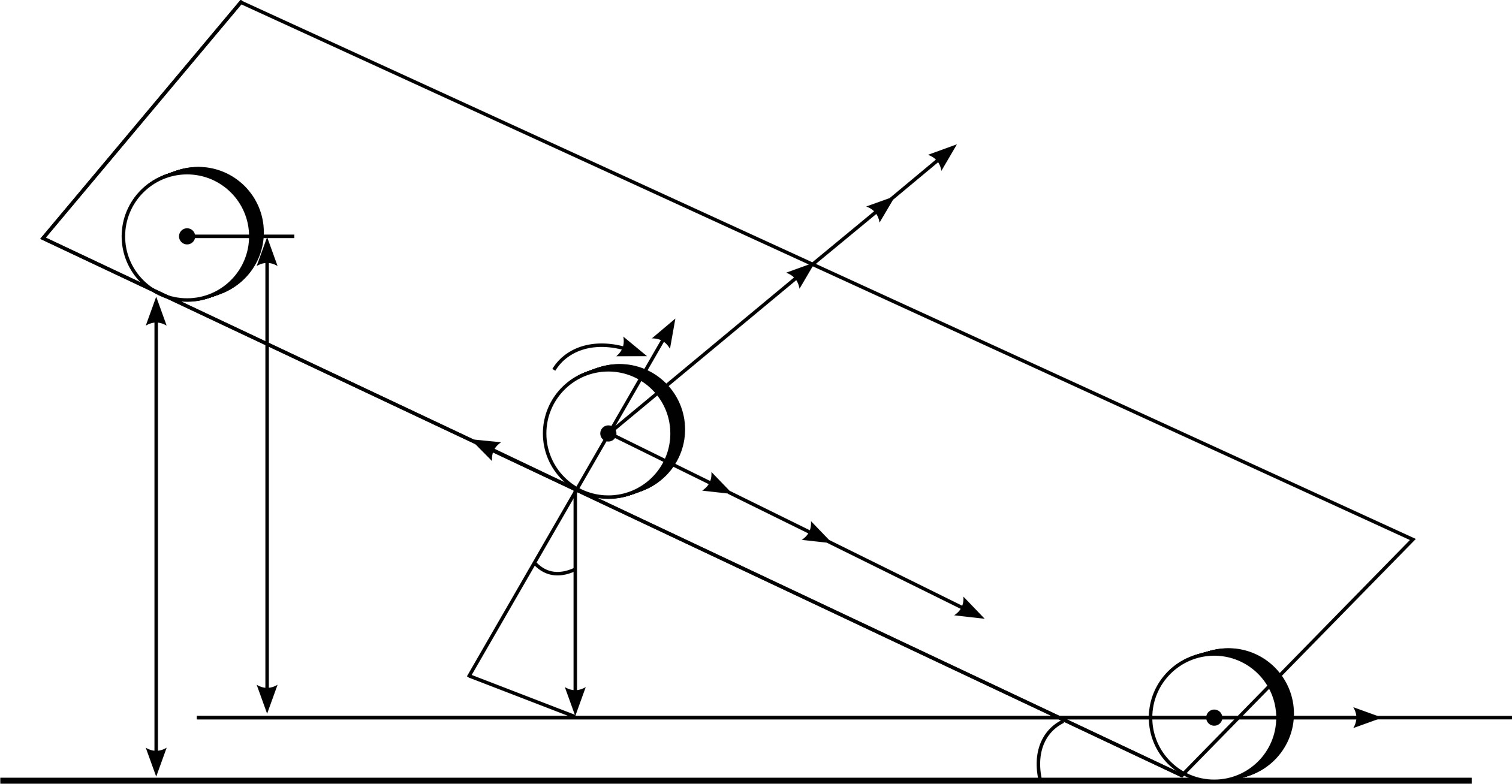
Качение – это сложное движение, которое является суммой двух простых: вращательного движения тела вокруг оси 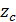 , проходящей через центр масс (ЦМ), и поступательного движения тела со скоростью, равной
, проходящей через центр масс (ЦМ), и поступательного движения тела со скоростью, равной 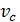 – скорости движения ЦМ. Центр масс механической системы или твердого тела – это точка С (рис. 13), которая в однородном поле тяжести совпадает с центром тяжести тела. Напомним, что центр тяжести тела – это точка, в которой приложена сила тяжести, равная
– скорости движения ЦМ. Центр масс механической системы или твердого тела – это точка С (рис. 13), которая в однородном поле тяжести совпадает с центром тяжести тела. Напомним, что центр тяжести тела – это точка, в которой приложена сила тяжести, равная 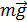 .
.
|
|
| α |
| α |
 0 0
|
|
|
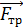
|
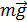
|
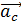
|
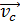
|
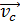
|
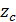
|
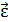
|
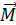
|
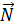
|
| С |
| С |
| С |
Рис. 13
Запишем закон динамики для вращательного движения диска вокруг оси 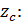
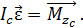 (1)
(1)
На диск действуют два тела: Земля – силой тяжести 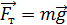 , и наклонная плоскость. Реакция этой опоры состоит из двух составляющих: силы нормальной реакции
, и наклонная плоскость. Реакция этой опоры состоит из двух составляющих: силы нормальной реакции 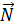 и силы трения
и силы трения 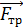 , которая не дает проскальзывать диску, а обеспечивает его качение. Силы
, которая не дает проскальзывать диску, а обеспечивает его качение. Силы 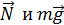 проходят через точку С, поэтому плечо каждой из них равно нулю, следовательно, моменты этих сил относительно оси
проходят через точку С, поэтому плечо каждой из них равно нулю, следовательно, моменты этих сил относительно оси 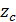 равны нулю. Момент создает только сила
равны нулю. Момент создает только сила 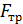 , для которой плечо равно радиусу диска R, а момент этой силы
, для которой плечо равно радиусу диска R, а момент этой силы
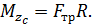 (2)
(2)
С учетом формулы (2) закон динамики (1) принимает следующий вид:
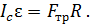 (3)
(3)
Так как в этом уравнении содержатся две неизвестных величины: угловое ускорение 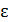 и сила трения, – то требуется еще одно уравнение. Это закон динамики поступательного движения центра масс (точки С), или теорема о движении ЦМ:
и сила трения, – то требуется еще одно уравнение. Это закон динамики поступательного движения центра масс (точки С), или теорема о движении ЦМ:
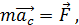 (4)
(4)
где 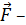 равнодействующая всех сил, приложенных к телу. В данной задаче
равнодействующая всех сил, приложенных к телу. В данной задаче
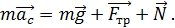 (4a)
(4a)
Проведем ось 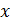 , направляя ее вдоль ускорения
, направляя ее вдоль ускорения 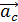 , и запишем уравнение (4а) в проекции на ось
, и запишем уравнение (4а) в проекции на ось 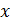 :
:
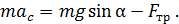 (5)
(5)
Далее решаем систему уравнений (3) и (5), но сначала установим связь углового ускорения диска 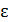 и линейного
и линейного 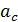 . В силу относительности движения ускорение точки С
. В силу относительности движения ускорение точки С 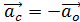 , где
, где 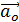 – ускорение перемещения точки О относительно точки С; модули этих ускорений одинаковы:
– ускорение перемещения точки О относительно точки С; модули этих ускорений одинаковы: 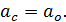 Из связи углового и линейного ускорения для вращения относительно оси
Из связи углового и линейного ускорения для вращения относительно оси 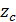 имеем
имеем 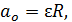 следовательно, исходя из равенства ускорений, получаем, что и величина
следовательно, исходя из равенства ускорений, получаем, что и величина
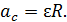 (6)
(6)
С учетом формулы (6) закон динамики (3) принимает следующий вид:
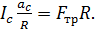 (7)
(7)
Из системы уравнений (5) и (7) нужно исключить неизвестную силу 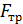 , для этого преобразуем уравнение (7), подставляя в него величину момента инерции диска
, для этого преобразуем уравнение (7), подставляя в него величину момента инерции диска 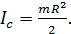 При этом уравнение (7) запишется так:
При этом уравнение (7) запишется так:
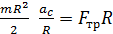 ;
; 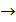
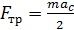 .
.
Подставим найденную величину силы 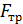 в уравнение (5):
в уравнение (5):
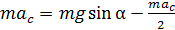 .
.
Выражая из полученного равенства ускорение 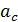 , получаем расчетную формулу для определяемой величины ускорения центра масс диска в виде:
, получаем расчетную формулу для определяемой величины ускорения центра масс диска в виде:
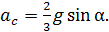 (8)
(8)
Вычисляем 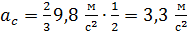 .
.
Для нахождения скорости точки С в конце скатывания диска с наклонной плоскости решаем кинематическую задачу. Из формулы (8) видим, что величина ускорения 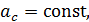 т. е. движение точки С равноускоренное; для такого движения скорость
т. е. движение точки С равноускоренное; для такого движения скорость
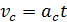 , (9)
, (9)
где t – время движения диска; это время найдем из другого уравнения кинематики равноускоренного движения, согласно которому путь, пройденный точкой С,
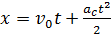 . (10)
. (10)
Преобразуем данное уравнение с учетом того, что 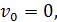 а из треугольника (см. рис. 11) имеем
а из треугольника (см. рис. 11) имеем 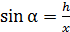 , что дает величину
, что дает величину 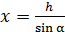 . Тогда, согласно уравнению (10), получаем
. Тогда, согласно уравнению (10), получаем
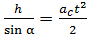 ,
, 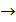
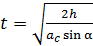 . (11)
. (11)
Подставим в уравнение (9) ускорение по формуле (8) и время скатывания по формуле (11). При этом получаем расчетную формулу:
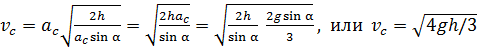 . (12)
. (12)
Вычислим величину скорости ЦМ диска: 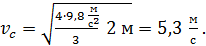
2-й путь решения задачи
Качение рассмотрим как вращение вокруг мгновенной оси вращения (МОВ). Этой осью (по свойству оси вращения, точки которой неподвижны) является линия касания диска с наклонной плоскостью, – эта линия проходит через точку О (см. рис. 13). В этой точке приложены силы реакции опоры – 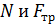 , причем, вторая их них явно неконсервативная, но моменты этих сил относительно МОВ равны нулю (плечо для них равно нулю). Благодаря этому силы реакции опоры не совершают работу, величина которой при вращательном движении
, причем, вторая их них явно неконсервативная, но моменты этих сил относительно МОВ равны нулю (плечо для них равно нулю). Благодаря этому силы реакции опоры не совершают работу, величина которой при вращательном движении 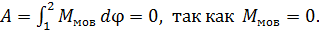 Сила тяжести
Сила тяжести 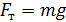 является консервативной, поэтому при качении выполняется закон сохранения механической энергии. Запишем ЗСМЭ, приравнивая
является консервативной, поэтому при качении выполняется закон сохранения механической энергии. Запишем ЗСМЭ, приравнивая 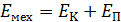 в двух положениях диска: 1 – вверху и 2 – внизу:
в двух положениях диска: 1 – вверху и 2 – внизу:
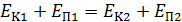 . (13)
. (13)
Здесь 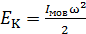 – кинетическая энергия вращения диска относительно МОВ,
– кинетическая энергия вращения диска относительно МОВ, 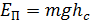 – потенциальная энергия, где
– потенциальная энергия, где 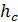 – высота, на которой находится точка С. Примем, что
– высота, на которой находится точка С. Примем, что 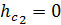 ; в этом случае имеем удобный нуль отсчета потенциальной энергии, так как
; в этом случае имеем удобный нуль отсчета потенциальной энергии, так как 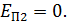 По рис. 13 видно, что
По рис. 13 видно, что 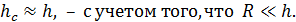 В положении 1 величина
В положении 1 величина 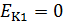 , так как диск начинает движение из состояния покоя. С учетом этих замечаний уравнение ЗСМЭ (13) запишется в следующем виде:
, так как диск начинает движение из состояния покоя. С учетом этих замечаний уравнение ЗСМЭ (13) запишется в следующем виде:
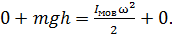 (14)
(14)
Величину момента инерции диска относительно МОВ найдем по теореме Штейнера, учитывая, что расстояние между осями 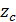 и МОВ равно R:
и МОВ равно R:
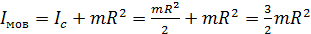 .
.
Подставляя величину 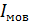 в уравнение (14), получаем равенство
в уравнение (14), получаем равенство
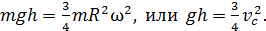 (15)
(15)
Здесь учтена связь линейной скорости точки С и угловой 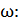
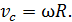
Выразим из равенства (15) линейную скорость точки С:
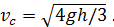
Отметим, что полученная формула совпадает с формулой (12), найденной выше путем совместного решения двух задач – динамической и кинематической. Для нахождения ускорения 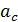 нужно прибегнуть к кинематической задаче, согласно которой из уравнения (9)
нужно прибегнуть к кинематической задаче, согласно которой из уравнения (9)
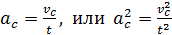 . (16)
. (16)
Из кинематической задачи (см. уравнение (11)) запишем:
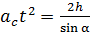 .
.
С учетом этого выражения формулу (16) перепишем в виде
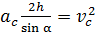 ;
; 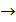
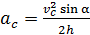 .
.
Подставляя в последнее выражение величину 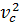 из формулы (15), получаем расчетную формулу для линейного ускорения ЦМ диска в виде
из формулы (15), получаем расчетную формулу для линейного ускорения ЦМ диска в виде
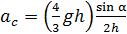 ;
; 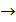
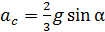 .
.
Полученная расчетная формула совпадает с формулой (8), найденной из решения с использованием законов динамики поступательного и вращательного движения диска.
Естественно, что при решении задач контрольной работы достаточно использовать один из двух рассмотренных выше способов решения. Отметим, что и в одном, и в другом способе время движения определяется в решении кинематической задачи.
Задача 14. В центре платформы стоит человек и держит на вытянутых в стороны руках гири массой 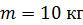 каждая. Расстояние гири от оси вращения
каждая. Расстояние гири от оси вращения 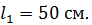 Платформа вращается с частотой
Платформа вращается с частотой 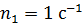 . Как изменится частота вращения платформы и какую работу произведет человек, если он сблизит руки, уменьшая расстояние каждой гири от оси вращения платформы до
. Как изменится частота вращения платформы и какую работу произведет человек, если он сблизит руки, уменьшая расстояние каждой гири от оси вращения платформы до 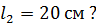 Суммарный момент инерции человека и платформы относительно оси вращения
Суммарный момент инерции человека и платформы относительно оси вращения  .
.
Дано Решение
 ; Рассмотрим систему тел «скамья – человек – гири»
; Рассмотрим систему тел «скамья – человек – гири»
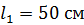 ; (рис. 14). В этой системе силы взаимодействия человека
; (рис. 14). В этой системе силы взаимодействия человека 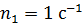 ; с гирями и со скамьей являются внутренними, и поэтому
; с гирями и со скамьей являются внутренними, и поэтому
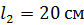 ; они не изменяют момент импульса системы.
; они не изменяют момент импульса системы.
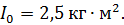 Внешние силы: сила тяжести и сила нормальной
Внешние силы: сила тяжести и сила нормальной
реакции опоры, – параллельны оси вращения z, поэтому 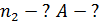 они не создают вращающего момента. Момент сил трения в оси
они не создают вращающего момента. Момент сил трения в оси 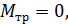 так как частота вращения
так как частота вращения 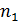 постоянна. Таким образом, моменты всех внешних сил относительно вертикальной оси вращения скамьи равны нулю. Следовательно, выполняется закон сохранения момента импульса системы в следующем виде:
постоянна. Таким образом, моменты всех внешних сил относительно вертикальной оси вращения скамьи равны нулю. Следовательно, выполняется закон сохранения момента импульса системы в следующем виде:
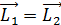 , или
, или 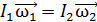 , (1)
, (1)
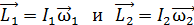 – моменты импульса системы относительно оси z, соответственно, до и после сближения гирь.
– моменты импульса системы относительно оси z, соответственно, до и после сближения гирь.
|
|
|
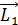
|
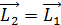
|
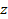
|
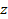
|
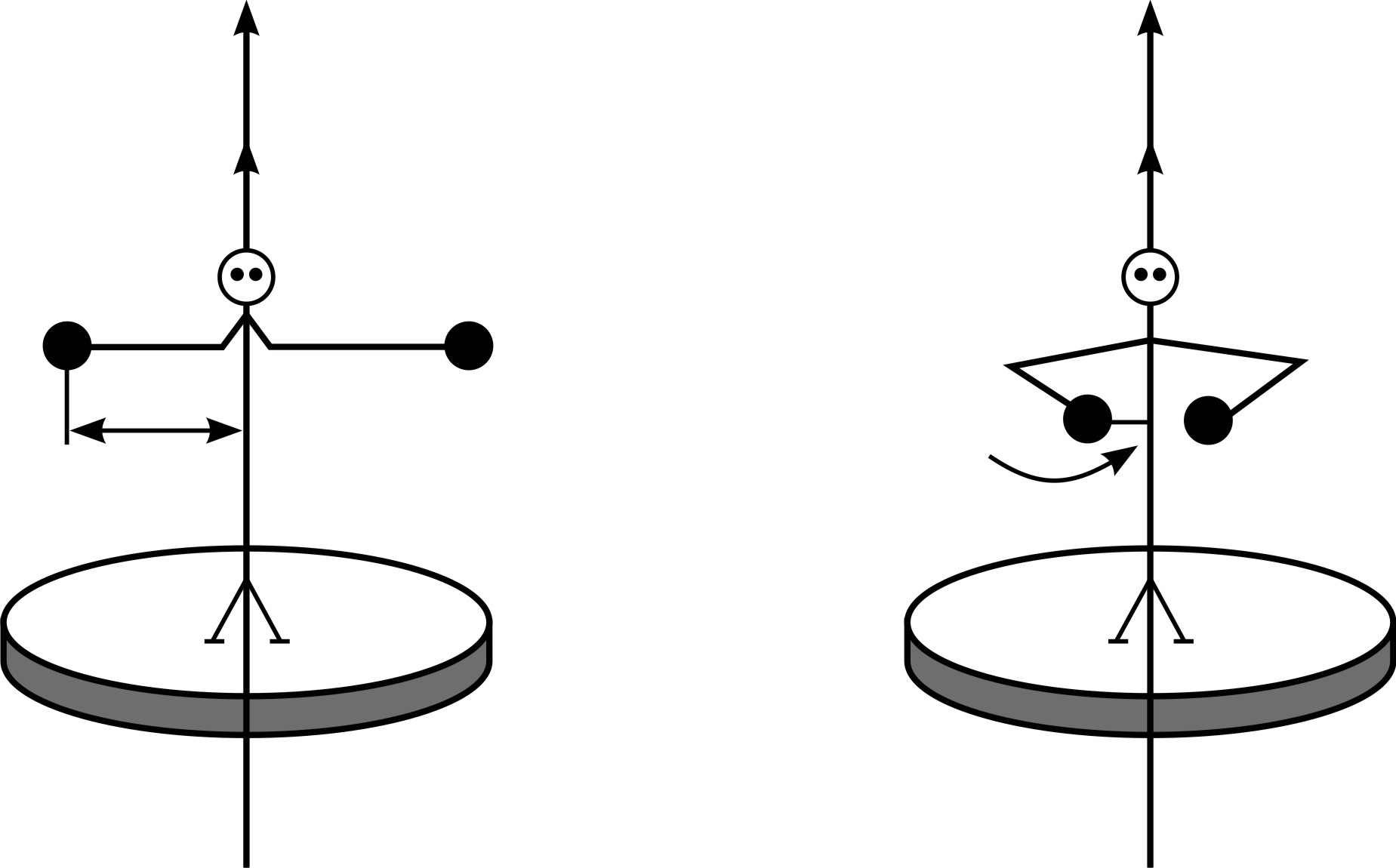 Запишем векторное уравнение (1) в проекции на ось вращения:
Запишем векторное уравнение (1) в проекции на ось вращения:
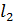
|
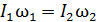 . (2)
. (2)
До сближения гирь момент инерции системы
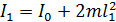 ,
,
а после сближения –
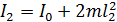 ,
,
| Рис. 14 |
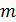 – масса каждой гири.
– масса каждой гири.
Используя связь угловой скорости
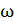 и частоты вращения
и частоты вращения 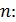
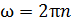 , (3)
, (3)
и подставляя величину 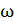 и значения моментов инерции в уравнение ЗСМИ (2), получаем следующее равенство:
и значения моментов инерции в уравнение ЗСМИ (2), получаем следующее равенство:
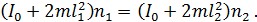
Из этого уравнения искомая частота вращения платформы
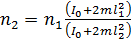 .
.
Вычисляем величину 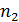 :
:
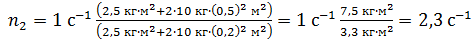 .
.
Перейдем к вычислению работы, которую произвел человек, сближая гири. Все перечисленные выше внешние силы не создают вращающего момента относительно оси и, следовательно, не совершают работы. Поэтому работу, совершенную человеком, можно найти как приращение кинетической энергии системы:
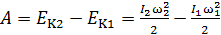 .
.
Подставляя угловую скорость 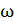 по формуле (3), получаем расчетную формулу в виде
по формуле (3), получаем расчетную формулу в виде
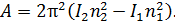 (4)
(4)
Вычислим работу, совершенную человеком при перемещении гирь, по формуле (4):
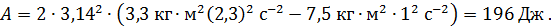
Задача 15. Человек массой 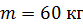 находится на неподвижной платформе массой
находится на неподвижной платформе массой 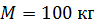 и радиусом
и радиусом 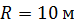 . Найдите угловую скорость, которую будет иметь платформа, если человек будет двигаться по окружности радиусом
. Найдите угловую скорость, которую будет иметь платформа, если человек будет двигаться по окружности радиусом 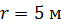 вокруг оси вращения со скоростью
вокруг оси вращения со скоростью 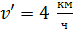 относительно платформы. Платформу можно считать однородным диском, а человека – точечной массой.
относительно платформы. Платформу можно считать однородным диском, а человека – точечной массой.
Дано
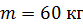 ; ;
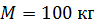 ; ;
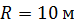 ; ;
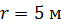 ; ;
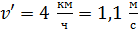 . .
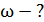
| Решение
На примере предыдущей задачи мы убедились, что для системы человек – платформа момент внешних сил относительно вертикальной оси равен нулю, и к системе применим закон сохранения момента импульса:
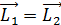 , (1)
где , (1)
где 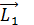 и и 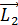 – начальный и конечный момент – начальный и конечный момент
|
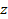
|
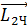
|
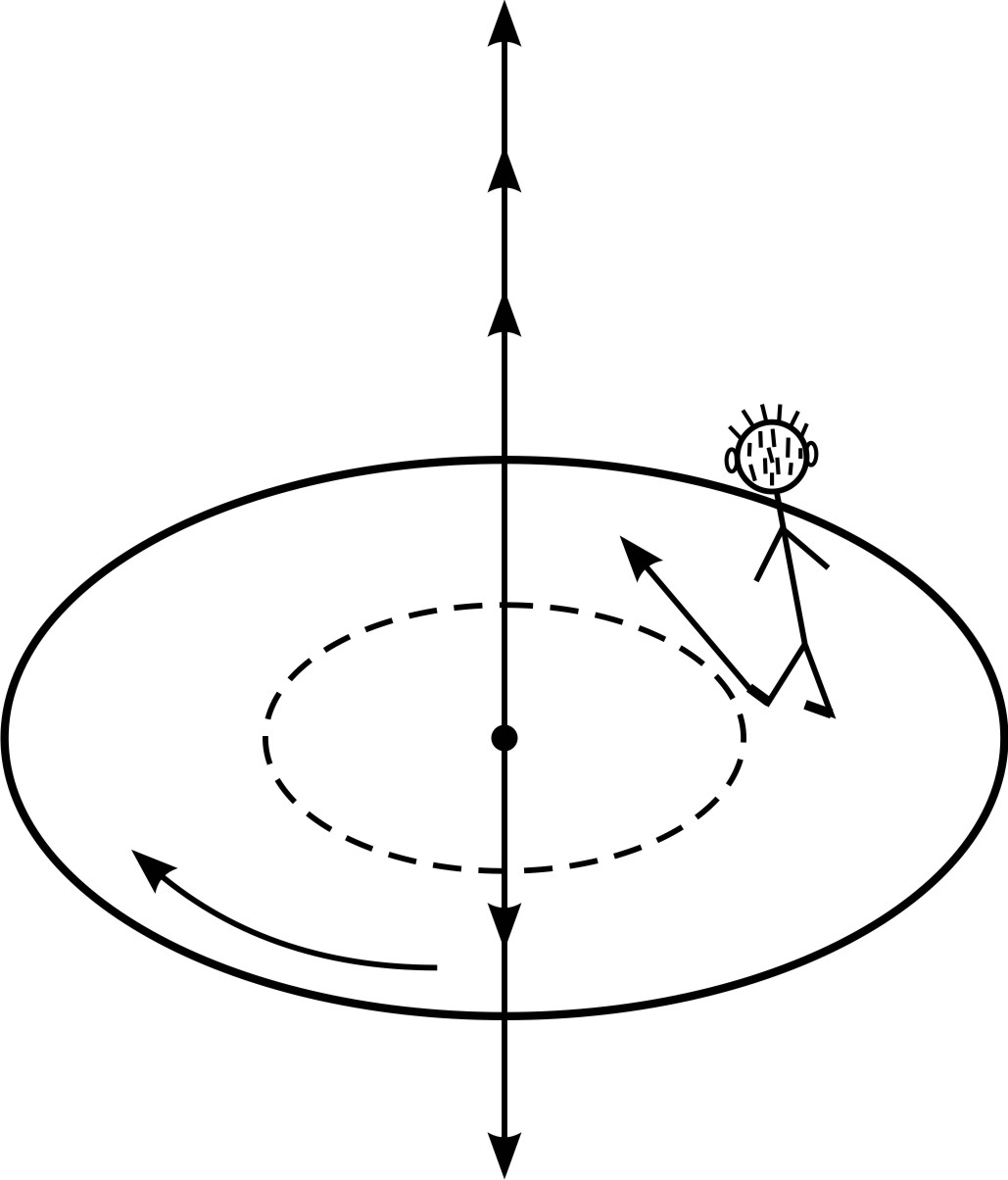
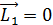 , (2)
, (2)
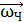
|
 Подставляя условие (2) в уравнение (1), получаем
Подставляя условие (2) в уравнение (1), получаем
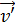
|
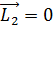 . (3)
. (3)
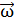
|

| Рис. 15 |
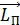 должен быть направлен противоположно моменту импульса человека
должен быть направлен противоположно моменту импульса человека 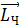 , т. е. платформа будет вращаться в сторону, противоположную движению человека (рис. 15).
, т. е. платформа будет вращаться в сторону, противоположную движению человека (рис. 15).
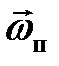
|
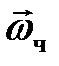
|
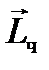
|
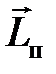
|
| Рис.13 |
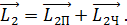
Перейдем от векторной записи к скалярной:
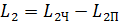 . (4)
. (4)
Учтем, что 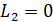 , тогда равенство (4) принимает следующий вид:
, тогда равенство (4) принимает следующий вид:
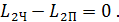 (5)
(5)
Здесь момент импульса человека рассчитываем как для материальной точки:
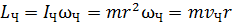 , (6)
, (6)
а 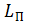 платформы – как диска:
платформы – как диска:
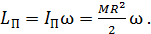 (7)
(7)
С учетом формул (6) и (7) уравнение (5) принимает следующий вид:
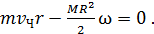 (8)
(8)
В уравнении (8) скорости человека и платформы указываются в одной системе отсчета, например, связанной с Землей, и условно принятой за неподвижную систему отсчета. В задаче дана скорость человека 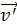 относительно движущейся платформы. Согласно закону сложения скоростей в классической механике, скорость тела
относительно движущейся платформы. Согласно закону сложения скоростей в классической механике, скорость тела 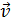 в системе, принятой за неподвижную, равна векторной сумме скоростей: скорости тела относительно движущейся системы
в системе, принятой за неподвижную, равна векторной сумме скоростей: скорости тела относительно движущейся системы 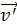 и скорости самой системы, в данном случае равной
и скорости самой системы, в данном случае равной 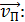
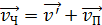 ,
,
или, в проекции на направление движения человека, получаем
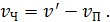 (9)
(9)
Здесь под 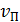 следует понимать линейную скорость тех точек платформы, по которым идет человек; эта скорость
следует понимать линейную скорость тех точек платформы, по которым идет человек; эта скорость
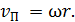 (10)
(10)
С учетом формул (9) и (10) уравнение (8) принимает следующий вид:
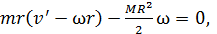
или 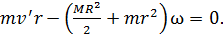 (11)
(11)
Запись ЗСМИ в виде уравнения (11) показывает, что человек участвует в двух движениях: движение «вперед» по платформе со скоростью 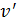 и вместе с платформой, вращающейся с угловой скоростью
и вместе с платформой, вращающейся с угловой скоростью 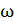 , человек «откатывается назад». Из уравнения (11) определяем скорость вращения платформы:
, человек «откатывается назад». Из уравнения (11) определяем скорость вращения платформы:
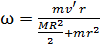 .
.
Вычисляем величину 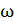 по этой формуле:
по этой формуле:
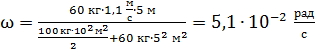 .
.
Механические колебания
Задача 16. Пружинный маятник жесткостью 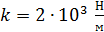 совершает гармонические колебания. Масса груза
совершает гармонические колебания. Масса груза 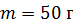 , максимальная скорость груза
, максимальная скорость груза 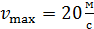 . Определите циклическую частоту
. Определите циклическую частоту 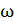 , период
, период 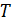 и амплитуду колебаний
и амплитуду колебаний 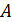 .
.
Дано Решение
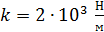 ; ;
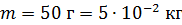 ; ;
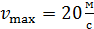 . .
| |
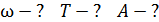
|
Циклическая частота 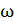 колебаний пружинного маятника определяется формулой
колебаний пружинного маятника определяется формулой
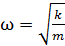 , (1)
, (1)
где k – жесткость пружины; m – масса груза.
Вычисляем частоту 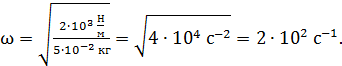
Период колебаний связан с циклической частотой формулой 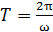 .
.
Вычисляем период колебаний 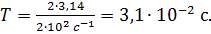
Амплитуду колебаний определим, рассчитывая полную механическую энергию груза, совершающего колебания:
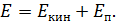 (2)
(2)
При колебаниях груза по закону 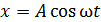 происходит превращение кинетической энергии в потенциальную, причем, в крайних положениях груза, когда смещение
происходит превращение кинетической энергии в потенциальную, причем, в крайних положениях груза, когда смещение 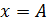 , скорость груза
, скорость груза 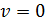 и величина
и величина 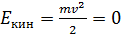 . Следовательно, согласно равенству (2), полная механическая энергия груза
. Следовательно, согласно равенству (2), полная механическая энергия груза
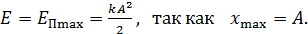 (3)
(3)
При движении груза из крайнего положения потенциальная энергия переходит в кинетическую энергию и в положении равновесия смещение 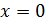 и потенциальная энергия
и потенциальная энергия 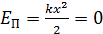 . При этом полная механическая энергия равна максимальной кинетической энергии груза:
. При этом полная механическая энергия равна максимальной кинетической энергии груза:
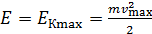 . (4)
. (4)
Приравняем значения полной механической энергии груза, определяемой формулами (3) и (4):
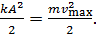 (5)
(5)
Из соотношения (5) выразим определяемую амплитуду колебаний груза
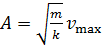 ; с учетом формулы (1) получаем
; с учетом формулы (1) получаем 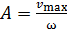 .
.
Вычисляем: 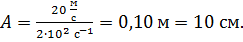
Задача 17. Частица массой 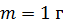 совершает гармонические колебания по закону
совершает гармонические колебания по закону 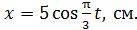 Определите период колебаний
Определите период колебаний 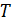 , максимальную скорость частицы
, максимальную скорость частицы 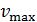 и ее механическую энергию
и ее механическую энергию 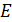 .
.
Дано Решение
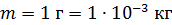 ; ;
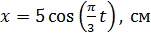 . .
| |
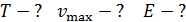
|
Запишем закон гармонических колебаний частицы в виде:
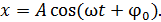 (1)
(1)
Сравнивая с заданным уравнением движения
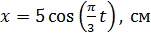 , (2)
, (2)
видим, что циклическая частота колебаний 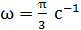 . Период колебаний связан с циклической частотой формулой
. Период колебаний связан с циклической частотой формулой
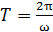 .
.
Подставляя в эту формулу найденное значение частоты, вычисляем:
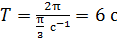 .
.
Скорость движения частицы определяем как первую производную от смещения 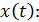
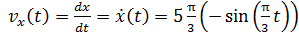 .
.
Получили гармонический закон колебаний величины скорости в виде
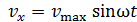 ,
,
где амплитуда скорости частицы 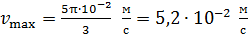 .
.
Полная механическая энергия E частицы, совершающей гармонические колебания (см. решение задачи 16) выражается формулой:
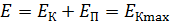 , или
, или 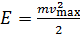 .
.
Вычисляем величину механической энергии колеблющейся частицы:
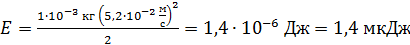 .
.
Задача 18. Материальная точка (МТ) массой m 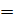 10 г совершает гармонические колебания по закону
10 г совершает гармонические колебания по закону 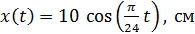 . Определите амплитуду
. Определите амплитуду 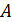 колебаний МТ, модуль ее скорости
колебаний МТ, модуль ее скорости 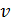 и силу
и силу 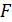 , действующую на МТ в момент времени
, действующую на МТ в момент времени 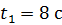 .
.
Дано Решение
m 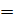 10 г 10 г 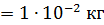 ; ;
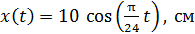 ; ;
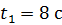 . .
|
|
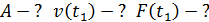
|
Запишем закон гармонических колебаний МТ в виде
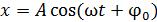 (1)
(1)
и сравним с заданным законом движения:
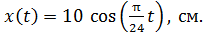 (2)
(2)
Из сопоставления уравнений (1) и (2) видим, что амплитуда колебаний 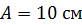 .
.
Скорость МТ найдем как первую производную от зависимости координаты от времени 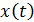 , представленной уравнением (2):
, представленной уравнением (2):
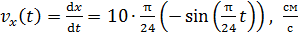 . (3)
. (3)
Вычислим по уравнению (3) значение скорости в момент времени 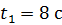 :
:
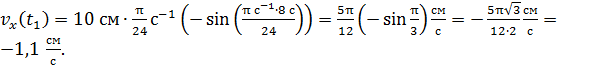
Знак «минус» – отрицательная проекция скорости на ось x, означает, что вектор скорости 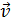 колеблющейся материальной точки в момент времени
колеблющейся материальной точки в момент времени 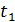 направлен противоположно оси
направлен противоположно оси 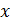 .
.
Силу, действующую на МТ, найдем по закону динамики движения – по второму закону Ньютона:
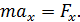 (4)
(4)
Для определения ускорения материальной точки (точнее, его проекции на ось x) используем определительную формулу:
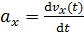 ,
,
где зависимость 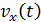 представлена уравнением (3); дифференцируя его, получаем проекцию ускорения на ось
представлена уравнением (3); дифференцируя его, получаем проекцию ускорения на ось 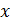 , как функцию времени:
, как функцию времени:
 ,
, 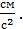 (5)
(5)
Подставляя выражение (5) в формулу закона динамики (4), находим закон изменения силы при гармонических колебаниях МТ в виде:
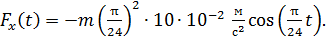 (6)
(6)
С учетом закона колебаний (2) уравнение (6) запишем в следующем виде:
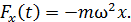 (7)
(7)
Уравнения (6) и (7) показывают, что упругая (или подобная ей сила) изменяется с течением времени по гармоническому закону, как и величина смещения МТ от положения равновесия.
Вычисляем величину проекции силы, действующей на колеблющуюся МТ в момент времени 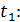
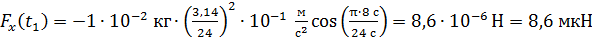 .
.
ЧАСТЬ 2
Дата: 2018-11-18, просмотров: 838.

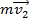
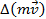
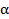
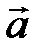
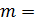 2 кг;
2 кг;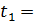 3 с;
3 с;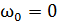 ;
;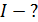
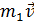
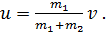 (1)
(1)