Закон сохранения момента импульса (ЗСМИ) можно применять к любой механической системе при условии, что результирующий момент всех внешних сил, приложенных к системе, равен нулю 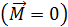 . Формулировка закона: Момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени:
. Формулировка закона: Момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени:
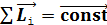 .
.
Здесь записана сумма векторов моментов импульса всех частей системы.
Напомним, что момент импульса твердого тела равен произведению его момента инерции на угловую скорость: 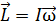 , – а момент импульса системы тел есть векторная сумма моментов импульса всех тел данной системы:
, – а момент импульса системы тел есть векторная сумма моментов импульса всех тел данной системы:
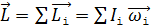 .
.
Закон сохранения механической энергии
Закон сохранения механической энергии (ЗСМЭ): полная механическая энергия системы тел сохраняется, если на тела системы действуют только консервативные силы (внутри и извне), а диссипативные силы отсутствуют или их работа равна нулю:
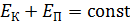 ,
,
где 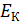 – кинетическая энергия, равная сумме энергий всех тел системы,
– кинетическая энергия, равная сумме энергий всех тел системы, 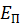 – потенциальная энергия системы.
– потенциальная энергия системы.
Консервативными являются силы, работа которых зависит только от закона сил и от начального и конечного положения тела; работа консервативных сил равна убыли потенциальной энергии системы. Консервативными являются сила тяжести, сила упругости 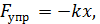 гравитационная сила. Диссипативными являются силы трения и сопротивления, приводящие к превращению механической энергии во внутреннюю энергию тел путем их нагрева.
гравитационная сила. Диссипативными являются силы трения и сопротивления, приводящие к превращению механической энергии во внутреннюю энергию тел путем их нагрева.
ЗСМЭ является частным случаем закона сохранения энергии системы: вследствие действия диссипативных сил происходит превращение кинетической энергии тел в эквивалентное количество других видов энергии, не связанных с механическим движением тел, например, в энергию теплового движения молекул.
Механические колебания
Гармонические колебания описывают уравнением:
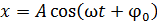 ,
,
где x – смещение колеблющейся точки относительно положения равновесия в момент времени t; 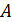 – наибольшее смещение, или амплитуда колебаний; w – циклическая частота колебаний; j0 – начальная фаза колебаний;
– наибольшее смещение, или амплитуда колебаний; w – циклическая частота колебаний; j0 – начальная фаза колебаний; 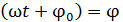 – фаза колебаний в момент времени t.
– фаза колебаний в момент времени t.
Колебания характеризуют частотой w и периодом T, связанными друг с другом соотношением: 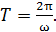
Период колебаний математического маятника
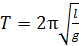 ,
,
где 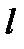 – длина маятника;
– длина маятника; 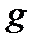 – ускорение свободного падения.
– ускорение свободного падения.
Период колебаний пружинного маятника
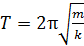 ,
,
где m – масса груза; k – жесткость пружины.
Кинетическая энергия гармонических колебаний
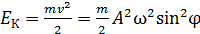 ,
,
где m – масса колеблющегося объекта; 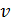 – его скорость.
– его скорость.
Потенциальная энергия гармонических колебаний
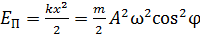 ,
,
где 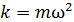 – жесткость, или коэффициент упругости пружины.
– жесткость, или коэффициент упругости пружины.
Результатом сложения одинаково направленных гармонических колебаний равной частоты является также гармоническое колебание с периодом, равным периоду складываемых колебаний. Если уравнения двух складываемых колебаний:
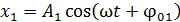 ,
,
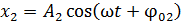 ,
,
то уравнение результирующего колебания:
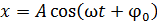 .
.
Здесь амплитуда результирующего колебания
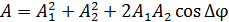 ,
,
где 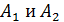 – амплитуды складываемых колебаний;
– амплитуды складываемых колебаний; 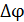 – их разность фаз.
– их разность фаз.
Уравнение затухающего колебательного движения имеет вид
 .
.
Здесь 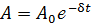 является амплитудой затухающих колебаний;
является амплитудой затухающих колебаний; 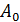 –начальная амплитуда (в момент времени
–начальная амплитуда (в момент времени 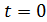 ); d – коэффициент затухания, его величина
); d – коэффициент затухания, его величина 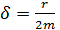 , где r – коэффициент сопротивления среды; m – масса колеблющейся точки. Затухание колебаний характеризуют логарифмическим декрементом затухания
, где r – коэффициент сопротивления среды; m – масса колеблющейся точки. Затухание колебаний характеризуют логарифмическим декрементом затухания
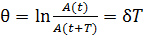 ,
,
где 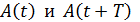 – амплитуды двух последовательных колебаний, отделенных друг от друга периодом колебаний T.
– амплитуды двух последовательных колебаний, отделенных друг от друга периодом колебаний T.
Циклическая частота затухающих колебаний
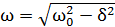 ,
,
где 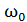 – циклическая частота свободных (собственных) незатухающих колебаний той же колебательной системы.
– циклическая частота свободных (собственных) незатухающих колебаний той же колебательной системы.
РЕКОМЕНДАЦИИ К РЕШЕНИЮ ФИЗИЧЕСКИХ ЗАДАЧ
1. Текст задачи следует внимательно прочитать, чтобы выяснить, какое движение (поступательное, вращательное, качение) или физическое явление рассматривается в задаче. Полезно сделать схематический чертеж или рисунок.
2. В разделе 1 – «Теоретическая часть» изучите сведения о рассматриваемом в задаче явлении: ознакомьтесь с основными формулами и величинами. Выясните, нельзя ли применить законы сохранения (ЗСИ, ЗСМИ, ЗСМЭ) – для этого проверьте, выполняются ли в задаче условия применения закона сохранения (замкнутость механической системы, консервативность сил). Выпишите законы и формулы, которые можно использовать при решении данной задачи.
3. Запишите краткое условие задачи, выбирая для обозначения заданных и искомых величин символы, которые использованы в формулах.
4. Задачу следует решать, как правило, в общем виде, т. е. получить расчетную формулу определяемой величины, содержащую символы заданных величин и физических постоянных.
5. Вычисление определяемой величины начинайте с подстановки в расчетную формулу значений величин. При этом следует помнить, что большинство физических величин имеют свои единицы измерения. Полезно записывать их при подстановке в формулу, чтобы убедиться, что все величины взяты в единицах СИ. Только при вычислении отношений, например, 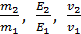 и т. п. можно подставлять величины в любых, но одинаковых единицах, т. е. не обязательно в СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей начинайте, закончив вычисление предыдущей определяемой величины.
и т. п. можно подставлять величины в любых, но одинаковых единицах, т. е. не обязательно в СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей начинайте, закончив вычисление предыдущей определяемой величины.
6. Полезно выполнять проверку расчетной формулы на совпадение единиц измерения левой и правой части равенства. Несовпадение единиц указывает на ошибку в расчетной формуле.
7. Вычисления и запись результата делайте с точностью до двух или трех (не более) значащих цифр. Незначащие нули записывайте в виде сомножителя 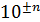 . При этом, если показатель степени n соответствует приставке, то используйте её: например,
. При этом, если показатель степени n соответствует приставке, то используйте её: например, 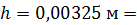
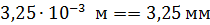 ;
; 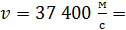 3,74
3,74 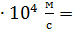 37,4
37,4 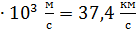 . Помните, что точность результата вычислений не может быть выше, чем точность исходных данных.
. Помните, что точность результата вычислений не может быть выше, чем точность исходных данных.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Дата: 2018-11-18, просмотров: 819.