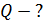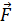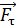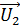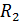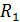Расчет приращения энтропии
Энтропия – это такая функция состояния термодинамической системы, дифференциал которой
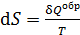 . (31)
. (31)
Здесь 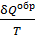 – приведенное количество теплоты, где
– приведенное количество теплоты, где 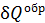 – бесконечно малое количество теплоты, сообщаемое телу при температуре T. Из формулы (31) следует, что единица измерения энтропии – 1
– бесконечно малое количество теплоты, сообщаемое телу при температуре T. Из формулы (31) следует, что единица измерения энтропии – 1 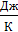 .
.
Второе начало термодинамики, как закон возрастания энтропии:
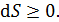
Энтропия замкнутой термодинамической системы возрастает ( 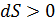 ), если в системе идут необратимые процессы, и не изменяется (
), если в системе идут необратимые процессы, и не изменяется ( 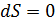 ) при равновесии. Замкнутой является термодинамическая система, которая не обменивается энергией с окружающей средой, т. е. для нее
) при равновесии. Замкнутой является термодинамическая система, которая не обменивается энергией с окружающей средой, т. е. для нее 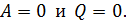
Энтропия незамкнутой системы может изменяться любым образом (убывать, возрастать, оставаться постоянной) в соответствии с формулой (31); например, если 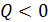 , т. е. система отдает теплоту, то и
, т. е. система отдает теплоту, то и 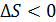 , что означает уменьшение энтропии системы, но при
, что означает уменьшение энтропии системы, но при 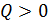 величина
величина 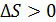 и энтропия системы возрастает.
и энтропия системы возрастает.
Энтропия является аддитивной величиной: энтропия системы равна сумме энтропий тел, входящих в систему. Например, энтропия смеси двух газов, а также ее приращение 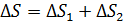 , – равно сумме приращений энтропии первого и второго компонентов смеси.
, – равно сумме приращений энтропии первого и второго компонентов смеси.
В соответствии с определительной формулой (31) для адиабатного процесса ( 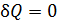 ) имеем
) имеем 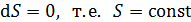 ; следовательно, обратимый адиабатный процесс протекает при постоянной энтропии. Поэтому адиабатный процесс называют изоэнтропийным.
; следовательно, обратимый адиабатный процесс протекает при постоянной энтропии. Поэтому адиабатный процесс называют изоэнтропийным.
Расчет приращения энтропии 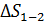 при переходе системы из состояния 1 в состояние 2 ведется путем суммирования бесконечно малых приращений
при переходе системы из состояния 1 в состояние 2 ведется путем суммирования бесконечно малых приращений 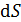 с учетом формулы (31):
с учетом формулы (31):
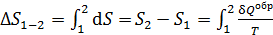 , (32)
, (32)
где величина 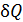 , согласно формуле (21):
, согласно формуле (21):
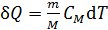 .
.
В изобарном процессе приращение энтропии
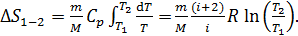 (33)
(33)
В изохорном процессе аналогично:
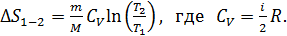 (34)
(34)
В изотермическом процессе, с учетом первого закона ТД в виде 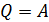 и формулы для работы, находим
и формулы для работы, находим
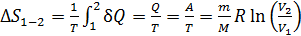 .
.
При фазовых переходах, протекающих при постоянной температуре T, в соответствии с формулой (32), получаем
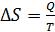 , (35)
, (35)
где 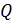 – теплота фазового перехода. Например, для плавления льда
– теплота фазового перехода. Например, для плавления льда
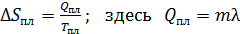 ,
,
где λ – удельная (на 1 кг массы) теплота плавления льда.
| Рис. 19 |
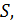
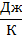
|
|
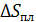
|
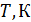
|
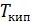
|
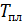
|
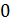
|
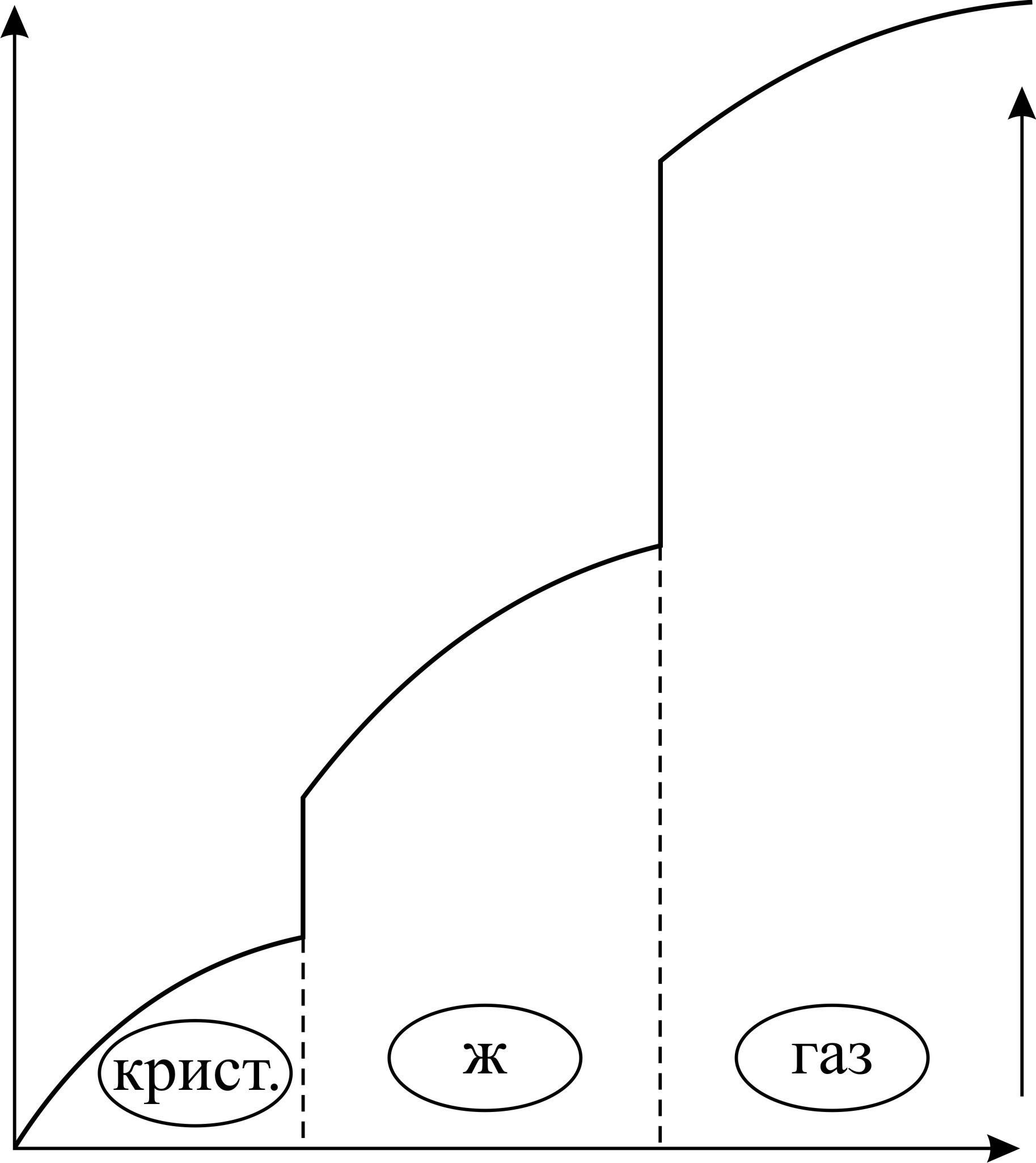 Результаты расчета по формулам (34) и (35) показаны на графике (рис. 19). График зависимости
Результаты расчета по формулам (34) и (35) показаны на графике (рис. 19). График зависимости 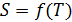 начинается практически в точке (0;0), так как третье начало термодинамики (теорема Нернста– Планка) утверждает, что энтропия всех тел стремится к нулю при приближении температуры
начинается практически в точке (0;0), так как третье начало термодинамики (теорема Нернста– Планка) утверждает, что энтропия всех тел стремится к нулю при приближении температуры 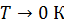 . В направлении, показанном стрелкой (справа от графика
. В направлении, показанном стрелкой (справа от графика 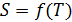 ), по мере возрастания температуры происходит увеличение энтропии вещества. При этом увеличивается объем системы и с увеличением температуры возрастает скорость движения молекул. Следовательно, растет хаотичность («беспорядок») как в расположении молекул в объеме вещества, так и в движении молекул.
), по мере возрастания температуры происходит увеличение энтропии вещества. При этом увеличивается объем системы и с увеличением температуры возрастает скорость движения молекул. Следовательно, растет хаотичность («беспорядок») как в расположении молекул в объеме вещества, так и в движении молекул.
РЕКОМЕНДАЦИИ К РЕШЕНИЮ ЗАДАЧ ПО РАЗДЕЛУ «МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА»
1. Текст задачи следует внимательно прочитать, чтобы выяснить, какое физическое явление или процесс рассматривается в задаче. Полезно сделать схематический рисунок или график процесса.
2. Ознакомьтесь с основными формулами для данного явления. Выпишите законы и формулы, которые можно использовать при решении данной задачи.
3. Запишите краткое условие задачи, выбирая для обозначения заданных и искомых величин символы, которые использованы в формулах.
4. Задачу следует решать, как правило, в общем виде, чтобы получить расчетную формулу определяемой величины.
5. Вычисление определяемой величины начинайте с подстановки в расчетную формулу значений величин. При этом полезно записывать и единицы измерения физических величин, чтобы убедиться, что все величины взяты в единицах СИ. Если определяемых величин несколько, то вывод расчетной формулы для следующей начинайте, закончив вычисление предыдущей определяемой величины.
6. Полезно выполнять проверку расчетной формулы на совпадение единиц измерения левой и правой части равенства. Несовпадение единиц указывает на ошибку в расчетной формуле.
7. Вычисления и запись результата делайте с точностью до двух или трех (не более) значащих цифр. Незначащие нули записывайте в виде сомножителя 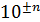 . При этом, если показатель степени n соответствует приставке, то используйте её: например,
. При этом, если показатель степени n соответствует приставке, то используйте её: например, 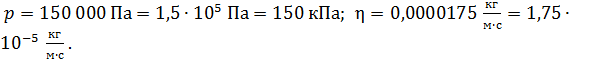 Помните, что точность результата вычислений не может быть выше, чем точность исходных данных.
Помните, что точность результата вычислений не может быть выше, чем точность исходных данных.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Молекулярная физика
Методика решения задач
1. Выписываем заданные в условии задачи величины, не забывая при этом вычислять термодинамическую температуру 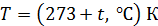 , а давление газа выражаем в паскалях (
, а давление газа выражаем в паскалях ( 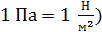 : 1 мм рт. ст.
: 1 мм рт. ст. 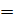 133 Па; 1 атм
133 Па; 1 атм 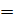 1,013
1,013 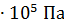 .
.
2. Если в расчетной формуле определяемая величина выражается через независимые характеристики молекул и параметры газа (например, при расчете теплопроводности, вязкости и коэффициента диффузии газов), то желательно вычислить отдельно характеристики молекул, чтобы конечная формула была не слишком громоздкой. К тому же при таких промежуточных расчетах можно проконтролировать правильность вычисляемых величин (см. п. 3).
3. Для проверки правильности вычисляемых величин сравните их по порядку величины со следующими значениями: при температуре 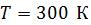 средняя скорость молекул воздуха (
средняя скорость молекул воздуха ( 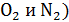 имеет порядок
имеет порядок 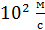 , а для «лёгких» молекул
, а для «лёгких» молекул 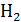 и He –
и He – 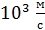 ; с увеличением температуры скорость молекул увеличивается, так как
; с увеличением температуры скорость молекул увеличивается, так как 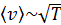 . Средняя энергия одной молекулы при
. Средняя энергия одной молекулы при 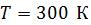 – весьма малая величина, ее порядок
– весьма малая величина, ее порядок 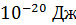 , а с ростом температуры она увеличивается пропорционально T . Средняя длина свободного пробега молекул при давлении газа
, а с ростом температуры она увеличивается пропорционально T . Средняя длина свободного пробега молекул при давлении газа 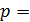 100 кПа имеет порядок
100 кПа имеет порядок 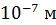 , но при уменьшении давления она возрастает:
, но при уменьшении давления она возрастает: 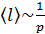 . Число молекул, содержащихся в 1
. Число молекул, содержащихся в 1 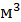 любого газа (или концентрация молекул) при нормальных условиях:
любого газа (или концентрация молекул) при нормальных условиях: 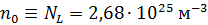 (число Лошмидта). Плотность воздуха при нормальных условиях
(число Лошмидта). Плотность воздуха при нормальных условиях 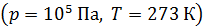 ρ
ρ 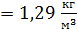 , но она изменяется пропорционально давлению газа и обратно пропорционально его температуре. Вязкость воздуха при нормальных условиях по порядку величины η
, но она изменяется пропорционально давлению газа и обратно пропорционально его температуре. Вязкость воздуха при нормальных условиях по порядку величины η 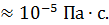
Задача 19. В сосуде находится смесь азота массой 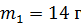 и гелия массой
и гелия массой 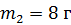 при температуре 27
при температуре 27 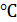 и давлении
и давлении 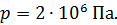 Определите: 1) количество молей смеси
Определите: 1) количество молей смеси 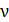 , 2) молярную массу смеси газов
, 2) молярную массу смеси газов 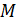 , 3) объем сосуда
, 3) объем сосуда 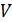 , 4) концентрацию молекул каждого газа
, 4) концентрацию молекул каждого газа 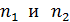 , 5) среднюю энергию молекулы каждого компонента смеси
, 5) среднюю энергию молекулы каждого компонента смеси 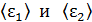 , 6) скорости молекул каждого газа: а) наиболее вероятную
, 6) скорости молекул каждого газа: а) наиболее вероятную 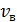 , б) среднюю квадратичную
, б) среднюю квадратичную 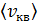 , в) среднюю арифметическую скорость
, в) среднюю арифметическую скорость 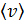 .
.
Решение
Газ при этих параметрах можно считать идеальным и использовать все законы и формулы молекулярно-кинетической теории идеального газа.
1) Количество газа 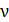 (число молей смеси), как и масса, является аддитивной величиной,– равной сумме числа молей компонентов смеси:
(число молей смеси), как и масса, является аддитивной величиной,– равной сумме числа молей компонентов смеси:
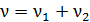 ,
,
здесь 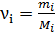 , где
, где 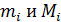 – соответственно, масса и молярная масса i-го компонента смеси.
– соответственно, масса и молярная масса i-го компонента смеси.
Вычисляем: 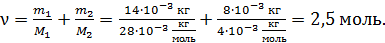
2) Найдем молярную массу 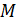 газовой смеси из формулы для числа молей смеси:
газовой смеси из формулы для числа молей смеси:
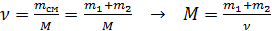 .
.
Вычисляем молярную массу газовой смеси:
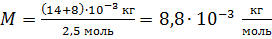 .
.
Дано
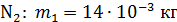 ; ;
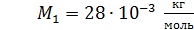 ; ;
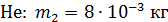 ; ;
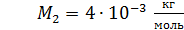 ; ;
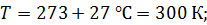
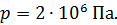
|
1) 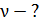 2) 2) 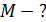 3) 3) 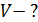 4)
4) 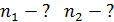 5)
5) 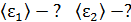 6)
6) 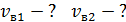
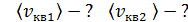
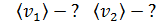
|
3) Объем газа 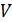 найдем из уравнения состояния идеального газа:
найдем из уравнения состояния идеального газа:
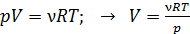 .
.
Вычисляем объем, занимаемый газом:
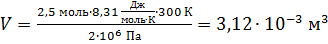 .
.
4) Концентрация i-го компонента газа 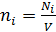 ; где
; где 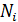 – число молекул данного компонента, равное
– число молекул данного компонента, равное 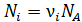 ; здесь
; здесь 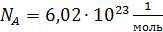 – число Авогадро.
– число Авогадро.
Вычисляем концентрации компонентов газовой смеси:
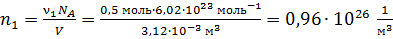 ;
;
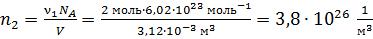 .
.
5) Средняя энергия молекулы 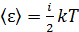 , где i – число степеней свободы молекулы газа; для двухатомной молекулы азота
, где i – число степеней свободы молекулы газа; для двухатомной молекулы азота 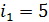 , а для одноатомной молекулы гелия
, а для одноатомной молекулы гелия 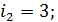
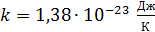 – постоянная Больцмана. Вычисляем среднюю энергию молекул
– постоянная Больцмана. Вычисляем среднюю энергию молекул
азота: 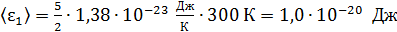 ;
;
гелия: 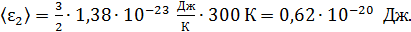
6) Рассчитываем скорости молекул компонентов газа – азота и гелия.
а) Наиболее вероятная скорость 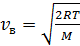 ;
;
для молекулы азота 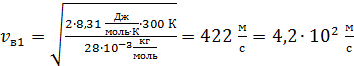 ;
;
для молекулы гелия 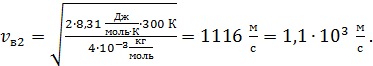
Видим, что молекулы с малой массой имеют большую скорость – при одинаковой температуре газа.
б) Средняя квадратичная скорость молекулы 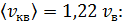
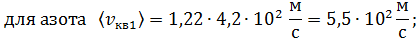
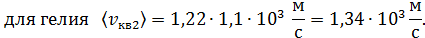
в) Средняя арифметическая скорость молекулы 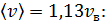
для азота 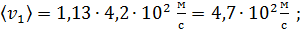
для гелия 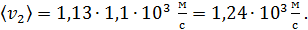
Задача 20. Термос высотой 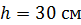 состоит из двух цилиндров, разделенных слоем воздуха. Радиус внешнего цилиндра
состоит из двух цилиндров, разделенных слоем воздуха. Радиус внешнего цилиндра 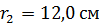 , радиус внутреннего –
, радиус внутреннего – 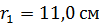 . Давление воздуха между стенками термоса
. Давление воздуха между стенками термоса 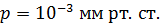 ; молярная масса
; молярная масса 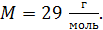 Термос наполнен чаем, температура которого
Термос наполнен чаем, температура которого 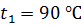 . Температура наружного воздуха
. Температура наружного воздуха 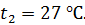 Какое количество теплоты переносится путем теплопроводности через боковую поверхность термоса за время
Какое количество теплоты переносится путем теплопроводности через боковую поверхность термоса за время 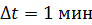 ? Эффективный диаметр молекул воздуха
? Эффективный диаметр молекул воздуха 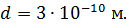
Дано Решение
Воздух: 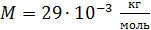 ; ;
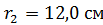 ; ;
|
Согласно уравнению Фурье для теплопроводности поток тепла
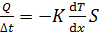 , (1)
, (1)
где ось x направлена вдоль переноса энергии, т. е. по радиальному направлению.
Будем рассматривать перенос через боковую поверхность цилиндра, имеющего средний радиус 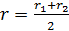 . Площадь этой боковой поверхности
. Площадь этой боковой поверхности
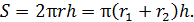 (2)
(2)
Градиент температуры
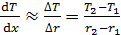 . (3)
. (3)
Согласно МКТ, теплопроводность идеального газа определяется формулой
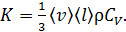 (4)
(4)
В этой формуле величины 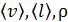 зависят от температуры газа, которая изменяется от
зависят от температуры газа, которая изменяется от 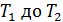 , поэтому найдем среднюю температуру газа
, поэтому найдем среднюю температуру газа 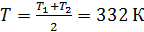 , для которой будем вычислять указанные параметры. В уравнении (4) скорости молекул
, для которой будем вычислять указанные параметры. В уравнении (4) скорости молекул 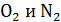 близки по величине, так как молярные массы этих компонентов воздуха различаются несущественно; поэтому, используя величину молярной массы M для воздуха, находим усредненную скорость молекул по формуле
близки по величине, так как молярные массы этих компонентов воздуха различаются несущественно; поэтому, используя величину молярной массы M для воздуха, находим усредненную скорость молекул по формуле
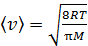 .
.
Так как в уравнение (4) входит несколько независимых величин, вычислим их по отдельности. Средняя арифметическая скорость молекул воздуха
 .
.
Средняя длина свободного пробега молекул 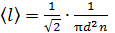 . Выразим концентрацию молекул n через давление газа, используя уравнение состояния идеального газа:
. Выразим концентрацию молекул n через давление газа, используя уравнение состояния идеального газа: 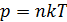 . Тогда формула для длины свободного пробега принимает следующий вид:
. Тогда формула для длины свободного пробега принимает следующий вид:
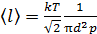 .
.
Вычисляем: 
Сравним эту величину 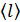 с расстоянием
с расстоянием 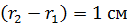 , которое пролетают молекулы в радиальном направлении от цилиндрической стенки радиусом
, которое пролетают молекулы в радиальном направлении от цилиндрической стенки радиусом 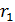 к стенке радиусом
к стенке радиусом 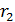 . Видим, что величина
. Видим, что величина 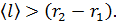 Такое состояние газа является высоким вакуумом для данного сосуда: в нем молекулы будут пролетать практически без соударений друг с другом от стенки внутреннего цилиндра к внешнему цилиндру. Следовательно, длина свободного пробега молекул
Такое состояние газа является высоким вакуумом для данного сосуда: в нем молекулы будут пролетать практически без соударений друг с другом от стенки внутреннего цилиндра к внешнему цилиндру. Следовательно, длина свободного пробега молекул
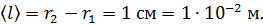
Плотность воздуха найдем, выражая ее из уравнения состояния идеального газа:
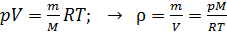 .
.
Вычисляем плотность воздуха: 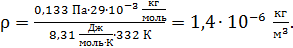
Заметим, что так как заданное в условии задачи давление воздуха 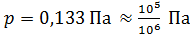 , т. е. в
, т. е. в 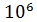 раз меньше, чем при нормальных условиях, то и плотность воздуха должна быть в
раз меньше, чем при нормальных условиях, то и плотность воздуха должна быть в 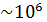 раз меньше, чем ρ
раз меньше, чем ρ 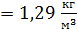 . Следовательно, величина плотности воздуха, находящегося между стенками термоса, определена верно.
. Следовательно, величина плотности воздуха, находящегося между стенками термоса, определена верно.
Удельная теплоемкость воздуха при постоянном объеме
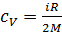 .
.
Так как молекулы воздуха 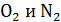 – двухатомные, то число степеней свободы этих молекул
– двухатомные, то число степеней свободы этих молекул 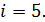 Вычисляем
Вычисляем
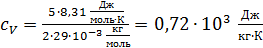 .
.
Вычислим теплопроводность воздуха по формуле (4), подставляя найденные значения величин:
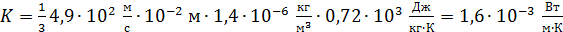 .
.
Сравнивая полученную величину K с теплопроводностью воздуха при нормальных условиях, равной 2,4 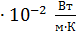 , видим, что теплопроводность воздуха в условиях вакуума на порядок (т. е. примерно в 10 раз) меньше. Следовательно, и поток тепла, переносимый через вакуумный слой воздуха, будет в ~10 раз меньше, чем при атмосферном давлении.
, видим, что теплопроводность воздуха в условиях вакуума на порядок (т. е. примерно в 10 раз) меньше. Следовательно, и поток тепла, переносимый через вакуумный слой воздуха, будет в ~10 раз меньше, чем при атмосферном давлении.
Запишем расчетную формулу для количества переносимой теплоты 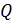 , выражая ее из уравнения (1) с учетом формул (2) и (3):
, выражая ее из уравнения (1) с учетом формул (2) и (3):
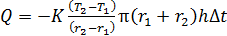 .
.
Вычисляем определяемую величину 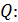
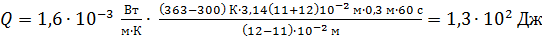 .
.
Задача 21. Для некоторого состояния водорода измерены величины коэффициента диффузии 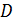 и вязкости газа
и вязкости газа 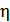 :
: 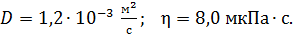 Найдите для этого состояния газа его плотность
Найдите для этого состояния газа его плотность 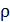 , концентрацию молекул
, концентрацию молекул 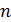 , среднюю длину свободного пробега молекул
, среднюю длину свободного пробега молекул 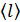 и их среднюю арифметическую скорость
и их среднюю арифметическую скорость 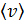 .
.
Решение
Запишем формулы МКТ для коэффициентов переноса: коэффициент диффузии
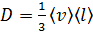 ; (1)
; (1)
вязкость газа
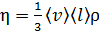 . (2)
. (2)
Дано 1) Сравнивая формулы (1) и (2), видим, что
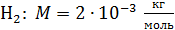 ; ;
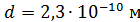 ; ;
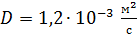 ; ;
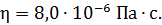
|
|
1) 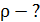 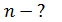 2)
2) 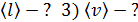
|
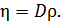
Из этого выражения определим плотность газа 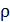
при данных условиях:
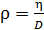 .
.
Вычисляем величину плотности водорода:
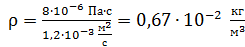 .
.
Концентрация молекул – это их число в единице объема, а плотность – масса этих молекул, находящихся в единице объема. Отсюда следует, что плотность газа 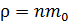 , где
, где 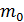 – масса одной молекулы; ее найдем, используя массу моля газа и число молекул в одном моле, равное числу Авогадро:
– масса одной молекулы; ее найдем, используя массу моля газа и число молекул в одном моле, равное числу Авогадро: 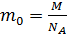 . Тогда концентрация молекул
. Тогда концентрация молекул
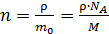 .
.
Вычисляем концентрацию молекул водорода:
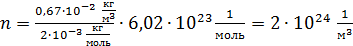 .
.
2) Длина свободного пробега молекул
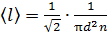 ,
,
где 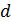 - эффективный диаметр молекулы газа.
- эффективный диаметр молекулы газа.
Вычисляем длину свободного пробега молекул водорода при данных условиях:
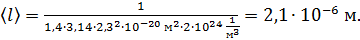
3) Скорость молекул газа зависит от его температуры, которая неизвестна в условии задачи. Но по формуле (1) для коэффициента диффузии можно определить среднюю скорость молекул
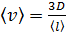 .
.
Вычисляем среднюю арифметическую скорость молекул водорода:
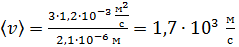 .
.
Задача 22. Пространство между двумя коаксиальными цилиндрами заполнено газом. Радиусы цилиндров 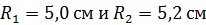 , их высота
, их высота 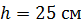 . Внешний цилиндр вращается с частотой
. Внешний цилиндр вращается с частотой 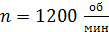 . Для того, чтобы внутренний цилиндр оставался неподвижным, к нему приложена касательная сила
. Для того, чтобы внутренний цилиндр оставался неподвижным, к нему приложена касательная сила 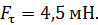 Определите вязкость газа, находящегося между цилиндрами.
Определите вязкость газа, находящегося между цилиндрами.
Дано Решение
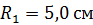 ; ;
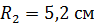 ;
h ;
h 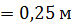 ; ;
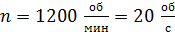 ; ;
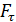 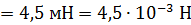 . .
| |
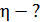
|
При вращении внешнего цилиндра слой воздуха вблизи цилиндра увлекается им и приобретает практически такую же линейную скорость U, как и скорость точек цилиндра:
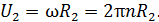
Благодаря внутреннему трению в газе импульс направленного движения со скоростью U передается соседним слоям газа и через них – внутреннему цилиндру. Для того, чтобы он не вращался, т. е. чтобы его момент импульса был 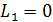 , а его приращение
, а его приращение 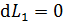 , в соответствии с уравнением динамики вращательного движения:
, в соответствии с уравнением динамики вращательного движения: 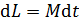 , – необходимо равенство нулю величины
, – необходимо равенство нулю величины 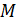 – момента всех сил, приложенных к цилиндру. Следовательно, силу вязкости F, действующую на цилиндр со стороны газа, необходимо компенсировать касательной силой
– момента всех сил, приложенных к цилиндру. Следовательно, силу вязкости F, действующую на цилиндр со стороны газа, необходимо компенсировать касательной силой 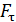 (рис. 20):
(рис. 20): 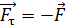 , – а модули этих сил равны, т. е.
, – а модули этих сил равны, т. е.
|
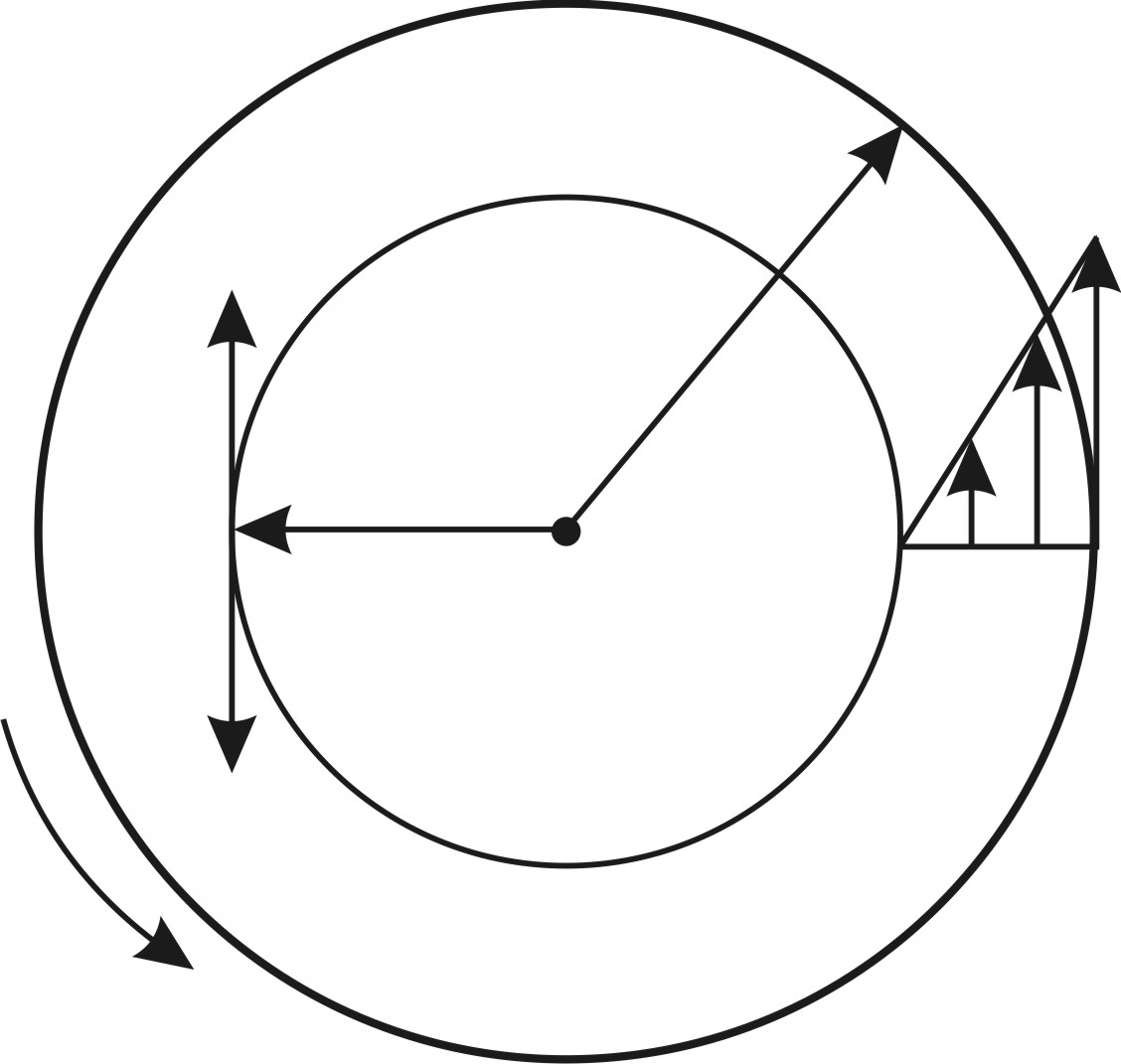
Рис. 20 |
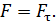 (1)
(1)
Согласно закону Ньютона, сила вязкости
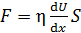 , (2)
, (2)
где η – вязкость газа; 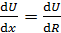 – градиент скорости движения слоев газа (ось x направлена вдоль радиуса цилиндров); S – площадь боковой поверхности внутреннего цилиндра, на который действует сила F. Учитывая малую величину зазора между цилиндрами, примем, что скорость U изменяется с расстоянием вдоль радиуса цилиндров по линейному закону: от
– градиент скорости движения слоев газа (ось x направлена вдоль радиуса цилиндров); S – площадь боковой поверхности внутреннего цилиндра, на который действует сила F. Учитывая малую величину зазора между цилиндрами, примем, что скорость U изменяется с расстоянием вдоль радиуса цилиндров по линейному закону: от 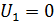 до
до 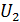 . Тогда модуль градиента скорости слоев газа
. Тогда модуль градиента скорости слоев газа
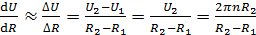 . (3)
. (3)
Площадь боковой поверхности внутреннего цилиндра
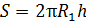 . (4)
. (4)
Определяемую величину вязкости газа выразим из уравнения (2):
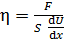 . (5)
. (5)
Подставим в это уравнение величины, согласно формулам (1), (3) и (4). При этом равенство (5) превращается в следующую расчетную формулу:
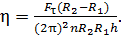 (6)
(6)
Вычисляем вязкость газа
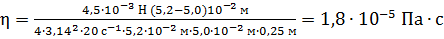 .
.
Задача 23. Определите внутреннюю энергию U водорода массой 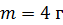 , а также среднюю кинетическую энергию
, а также среднюю кинетическую энергию 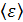 молекулы этого газа при температуре
молекулы этого газа при температуре 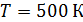 .
.
Дано Решение
H2 : 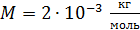 ; ;
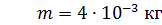 ; ;
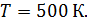
|
|
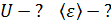
|
Внутренняя энергия идеального газа зависит от количества вещества, равного числу молей 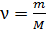 , от числа степеней свободы молекулы газа i и от его термодинамической температуры T, согласно уравнению:
, от числа степеней свободы молекулы газа i и от его термодинамической температуры T, согласно уравнению:
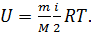 (1)
(1)
Для двухатомной молекулы водорода число степеней свободы 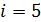 .
.
Вычислим значение U по уравнению (1):
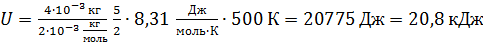 .
.
Средняя энергия одной молекулы 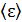 , согласно закону Больцмана о равномерном распределении энергии по степеням свободы молекулы:
, согласно закону Больцмана о равномерном распределении энергии по степеням свободы молекулы:
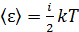 , (2)
, (2)
где 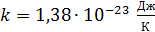 – постоянная Больцмана.
– постоянная Больцмана.
Вычисляем значение 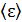 по формуле (2):
по формуле (2):
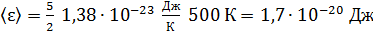 .
.
Задача 24. Определите среднюю квадратичную скорость 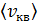 молекулы газа, находящегося в сосуде объемом
молекулы газа, находящегося в сосуде объемом 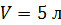 под давлением
под давлением 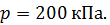 Масса газа
Масса газа 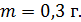
Дано Решение
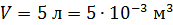 ; ;
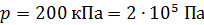 ; ;
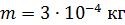 . .
|
|
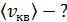
|
Средняя квадратичная скорость молекулы, по определению
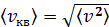 . (1)
. (1)
Величину среднего значения квадрата скорости находят из формулы среднего значения энергии поступательного движения молекулы:
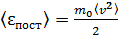 . (2)
. (2)
С другой стороны, согласно закону о равномерном распределении энергии по степеням свободы молекулы:
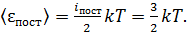 (3)
(3)
Приравнивая величину 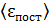 по формулам (2)
по формулам (2)
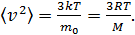 (4)
(4)
Подставляя величину 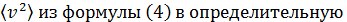 формулу (1), имеем
формулу (1), имеем
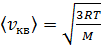 . (5)
. (5)
Параметры газа: давление 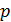 , объем
, объем 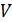 и термодинамическая температура
и термодинамическая температура 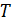 , – связаны уравнением состояния идеального газа:
, – связаны уравнением состояния идеального газа:
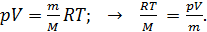 (6)
(6)
С учетом соотношения параметров газа (6) уравнение (5) преобразуется в расчетную формулу средней квадратичной скорости молекулы газа:
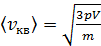 .
.
Вычисляем: 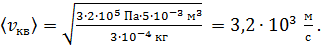
Задача 25. Для азота, находящегося при температуре 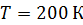 , определите среднюю кинетическую энергию поступательного движения молекулы
, определите среднюю кинетическую энергию поступательного движения молекулы 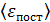 , среднюю энергию ее вращательного движения
, среднюю энергию ее вращательного движения 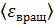 и среднее значение полной кинетической энергии молекулы
и среднее значение полной кинетической энергии молекулы 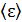 , а также молярную внутреннюю энергию газа
, а также молярную внутреннюю энергию газа 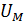 .
.
Дано Решение
N2: 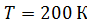 . .
|
1) 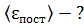 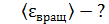 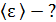 2)
2) 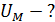
|
1) Согласно закону Больцмана о равномерном распределении энергии по степеням свободы молекулы, на каждую поступательную и вращательную степень свободы молекулы приходится одинаковая энергия 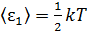 , где k –постоянная Больцмана; T – термодинамическая температура. Следовательно,
, где k –постоянная Больцмана; T – термодинамическая температура. Следовательно,

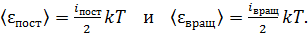 (1)
(1)
Двухатомная молекула азота имеет 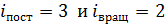 , а полное число степеней свободы молекулы азота равно их сумме:
, а полное число степеней свободы молекулы азота равно их сумме: 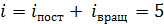 , так как при
, так как при 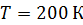 величина
величина 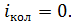 Тогда среднее значение полной кинетической энергии молекулы
Тогда среднее значение полной кинетической энергии молекулы
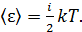 (2)
(2)
Вычисляем средние значения кинетической энергии молекулы азота по формулам (1) и (2):
энергия поступательного движения
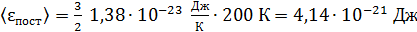 ;
;
энергия вращательного движения
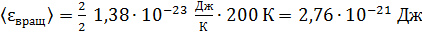 ;
;
полная кинетическая энергия молекулы, по свойству аддитивности энергии
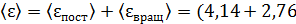 )
) 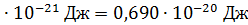 ;
;
и по формуле (2): 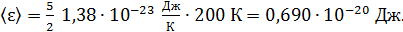
Видим, что результаты обоих расчетов одинаковы.
2) Молярная внутренняя энергия газа – это энергия одного моля вещества. В формуле
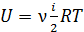 , полагаем
, полагаем 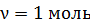 ; тогда
; тогда 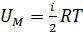 .
.
Вычисляем: 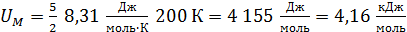 .
.
Термодинамика
Дата: 2018-11-18, просмотров: 772.
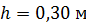 ;
;
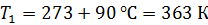 ;
;
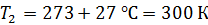 ;
;
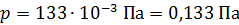 ;
;
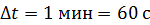 ;
;