Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

K = ∆/σ

Доверительная вероятность

t = 2 P = 95,5% t = 2,5 P = 98,6% t = 3,0 P = 99,7 % Ориентировочное знакомство 0,5 0,4 0,3 16 25 44 25 39 69 36 56 100 Исследование средней точности 0,2 100 156 225 Исследование повышенной точности 0,1 400 625 900

1.4.5. Пятое свойство статистической совокупности — взаимосвязь признаков в статистической совокупности

Пятое свойство статистической совокупности — это определе­ние взаимосвязи между признаками. В природе и обществе все процессы и явления взаимно связаны. Формами проявления количественных связей служат функциональная и корреляци­онная связи.

Функциональная связь характеризуется тем, что каждому зна­чению одного признака соответствует строго определенное зна­чение другого признака и изменение величины одного призна­ка неизбежно вызывает совершенно определенные изменения величины другого признака. Как правило, функциональная связь характерна для физико-химических явлений и присуща неживой природе: например, с возрастанием скорости увели­чивается пройденное расстояние.

При корреляционной связи каждому значению одного при­знака соответствует несколько значений другого признака, по­этому она проявляется лишь при массовом сопоставлении при­знаков в качественно однородной совокупности и характерна для социально-гигиенических и медико-биологических процессов. Например, при увеличении роста, как правило, возрас­тает масса тела человека, хотя могут встречаться высокие люди, но с дефицитом массы тела, и наоборот, при небольшом росте наблюдается избыточная масса тела.

Признаки могут быть качественными и количественными несгруппированными величинами (абсолютными и производ­ными). Главным является установление причинных взаимосвя­зей, подтверждающих зависимость одного явления от другого или от какой-то общей причины. С этой целью определяют ко­эффициент корреляции, который позволяет оценить характер, силу и достоверность взаимосвязи изучаемых признаков. По направлению связь между явлениями может быть прямой (+) и обратной (-). Если связь между признаками прямая, то с уве­личением одного признака увеличивается и другой. Например, чем старше ребенок, тем больше его рост; по мере снижения температуры тела, как правило, частота пульса уменьшается и т. д. При обратной связи между изучаемыми явлениями с уве­личением одного признака другой увеличиваться не будет. На­пример, с увеличением возраста снижается показатель средней продолжительности предстоящей жизни. В зависимости от чис­ленного выражения коэффициента корреляции различают связь слабую (от 0,0 до 0,3), среднюю (от 0,3 до 0,7) и сильную (от 0,7 до 1,0). Фактически, если коэффициент корреляции со­ставит 0,0, то это значит, что связь между явлениями отсутст­вует, а если коэффициент корреляции будет равен 1,0, то это свидетельствует о сильной и полной (или функциональной) связи между явлениями. Достоверность коэффициента корре­ляции определяется величиной ошибки и доверительным ко­эффициентом t. В том случае, если полученный коэффициент корреляции в 3 раза и более превышает свою ошибку, он счи­тается достоверным.

Для вычисления коэффициента корреляции используют мето­ды рангов, или метод Спирмена (р), квадратов, или метод Пир­сона (r), корреляционной решетки (η) и множественной кор­реляции. Наиболее простым методом является вычисление ко­эффициента корреляции методом рангов (метод Спирмена), но полученный коэффициент дает приближенные результаты. Для вычисления коэффициента корреляции данным методом ис­пользуют формулу:

Ρ_{xy = 1 -}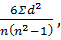

где d— разность рангов;

1 и 6 — постоянные коэффициенты;

п — число наблюдений сравниваемых пар.

Применение данной формулы предполагает обязательное ранжирование признаков в порядке их возрастания (или убывания)

 

                                                                                                       Таблица 13

Определение связи между ростом и массой тела у студентов-мужчин 20-22 лет по методу рангов

Число обследованных	Признаки		Ранги		Разность рангов
	Рост (x), см.	Масса тела (y), кг.	x	y	-y	d2
1 2 3 4 5 6 7 8 9 10 11 12 n = 12	169 170 171 174 176 180 181 184 185 185 187 188	55 61 62 68 75 75 81 78 71 80 81 82	1 2 3 4 5 6 7 8 9,5 9,5 11 12	1 2 3 4 6,5 6,5 10,5 8 5 9 10,5 12	0 0 0 0 -1,5 -0,5 -3,5 0 4,5 0,5 0,5 0	0 0 0 0 2,25 0,25 12,25 0 20,25 0,25 0,25 0 𝞢 = 35,5

 

Главным условием является соблюдение определенных правил:

• ранжировать каждую колонку цифр (вариант) нужно независимо от данных других столбцов;

• при ранжировании соблюдать единые требования, состоящие в том, что если в первой колонке вариант ранжирование начали с минимальной величины, то и во второй колонке цифр необходимо сделать также. Например, для определения взаимосвязи роста и массы тела были обследованы 12 студентов-мужчин в возрасте 20—22 года. Полученные данные представлены в табл. 13.

При определении порядкового номера следует учитывать, что при наличии одинаковых вариант им всем дается среднее значение тех рангов, которые они (варианты) занимают. Так, в данном примере две варианты роста имели одинаковое значение 185 см и занимали по порядку 9-е и 10-е места, при этом каждая варианта получила среднее значение приходящихся наних порядковых (ранговых) мест, равное 2J_!5 = 9,5. Аналогичным образом рассчитывали ранговые места для массы тела.

Подставляя полученные значения (d и п) в формулу, вычисляем коэффициент корреляции, он равен +0,876, что свидетельствует о наличии прямой и сильной зависимости между ростом и массой тела у студентов-мужчин в возрасте 20 - 22 года

Ρ_xy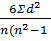= 1 -  = 1- 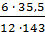 = 1- 0,124 = +0,876

Для определения достоверности полученного коэффициента корреляции вычисляют величину ошибки по формуле:

m_{p =}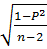

где m_p — средняя ошибка коэффициента корреляции, вычисленного методом рангов;

р — величина коэффициента корреляции, вычисленного методом рангов;

п — число наблюдений.

Величина ошибки коэффициента корреляции (р = +0,876).

Таким образом, вычисленный по методу рангов коэффициент корреляции, равный +0,876 ± 0,153, отражает наличие прямой, сильной и достоверной корреляционной зависимости и свидетельствует о том, что в целом с увеличением роста возрастает масса тела.

Метод рангов применяют в тех случаях, когда:

• число наблюдений не больше 30;

• признаки имеют не только количественное, но и качественное выражение (описательного характера);

• ряды распределения имеют открытые варианты (20 лет и более).

Наиболее точным и часто применяемым является метод квадратов или метод Пирсона:

r_{xy =} ,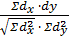

где ρ – коэффициент корреляции, вычисленный методом квадратов

d_{x –} отклонения вариант от средней величины (V_x – Mx)

d_{y -} отклонения вариант от средней величины(V_y- M_y)

Ошибку для коэффициента корреляции, вычисленного методом квадратов, определяют по формуле:

m_{r =}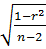

где m_{r -} ошибка коэффициента корреляции, вычисленного методом

квадратов;

п - число наблюдений.

При большом числе наблюдений (более 30 единиц) для определения коэффициента корреляции целесообразно применять метод корреляционной решетки, а при определении связи одновременно между тремя и более признаками используют метод множественной корреляции. При этом коэффициент корреляции (характер, сила и достоверность) оценивают по критериям, описанным ранее.

Метод стандартизации. При сравнении тех или иных общих показателей необходимо соблюдать важнейшее условие, которое заключается в однородности состава сравниваемых совокупностей по признаку, влияющему на величину этих показателей. Так, например, для того чтобы сопоставить летальность в двух больницах и сделать вывод, где она выше, следует прежде всего проанализировать, однороден ли в этих больницах состав больных по нозологическим формам болезни, по возрастному составу больных, по уровню оснащенности оборудованием и медикаментами и т. д.

Безусловно, в больнице, в которой среди госпитализированных больше лиц с тяжелыми хроническими заболеваниями, находящихся в более старших возрастных группах, будет выше общий показатель летальности. Разный состав пациентов в этих больницах делает несопоставимыми общие показатели летальности. Однако в ряде случаев не только в социально-гигиенических клинических исследованиях, а и в практическом здравоохранении нередко невозможно составить однородные группы для сравнения тех или иных показателей. Это касается,  прежде всего,  заболеваемости, рождаемости, общей смертности, а также показателей, характеризующих деятельность лечебно-профилактических учреждений в странах, областях, городах, районах внутри города, имеющих разный состав населения по возрасту, полу, исходному состоянию здоровья, условиям жизни и т. д. Например, при сравнении деятельности учреждений здравоохранения одним из ведущих показателей является число больных, выписанных из стационара с осложнениями. Так, в одной из больниц города этот показатель составил 3,4, а в другой — 3,7 на 100 больных. Но прежде чем сравнивать эти показатели и делать выводы, следует проанализировать совокупности, из которых они получены. В данном случае необходимо обратить внимание на распределение больных по отделениям. Преобладание терапевтических больных, как правило, способствует увеличению показателя, так как именно в это отделение госпитализируют тяжелобольных, нередко имеющих сочетанную патологию.

Для сравнения данных показателей, вычисленных из неоднородных по своему составу совокупностей, применяют специальный метод, который называется методом стандартизации.

Стандартизация — метод сравнения показателей в двух неоднородных совокупностях на основании расчета условных (стандартизованных) показателей при использовании стандарта.

Рассчитанные при помощи этого метода стандартизованные показатели условны, потому что они, косвенно устраняя влияние того или иного фактора на истинные показатели, указывают, какими были бы эти показатели, если бы влияние данного фактора, мешающего сравнению, отсутствовало.

Следовательно, стандартизованные показатели могут быть использованы только с целью сравнения. Существует несколько способов расчета стандартизованных показателей, среди которых различают прямой, косвенный и обратный методы. Наиболее распространенным является прямой метод.

Суть прямого метода состоит в вычислении общих стандартизованных показателей в сравниваемых совокупностях, которые уравновешены благодаря выбранному стандарту. Предварительно на I этапе вычисляют интенсивные показатели в каждой из сравниваемых совокупностей, по которым судят об истинной частоте изучаемого явления в исследуемых совокупностях. Следующий II этап заключается в выборе стандарта, за который можно принять сумму данных двух рассматриваемых совокупностей, или средний состав обеих групп, или одну из сравниваемых групп, или какую-то третью группу, близкую к сравниваемым данным одной из статистических совокупностей. Главное условие — стандарт должен быть одинаковым для сравниваемых совокупностей.

На III этапе рассчитывают условные величины в каждой группе стандарта и на IV этапе — общие стандартизованные показатели, которые тоже являются условными, гипотетическими. Целесообразно все последовательные расчетные операции по этапам стандартизации оформить в виде таблицы (табл.14).

                                                                                             Таблица 14

Распределение больных, выписанных с осложнениями в больницах

А и Б (данные условные)

Отделение

Больница А

Больница Б

I этап Интенсив Ные показа Тели  (на 100 больных)

II этап Выбор стандарта

III этап Дата: 2018-11-18, просмотров: 321. ⇐ Предыдущая12345678910Следующая ⇒ Материалы представленные на сайте исключительно с целью ознакомления пользователям Интернета и не преследуют коммерческих целей или нарушение авторских прав. © 2018 - 2024