При изучении генеральной (сплошной) совокупности для ее количественной характеристики достаточно рассчитать М и σ. Однако на практике, как правило, исследование проводят на выборочной совокупности, которая должна быть репрезентативна (достоверна) или представительна для генеральной совокупности. Репрезентативность выборочной совокупности оценивают специальными методами отбора, она означает представительность в ней всех учитываемых признаков генеральной совокупности.
Оценка достоверности результатов исследования базируется на теоретических основах репрезентативности и дает возможность достаточно обоснованно охарактеризовать выявленные закономерности. При определении достоверности результатов
исследования необходимо установить, с какой вероятностью можно перенести результаты изученных признаков выборочной совокупности (части явления) на всю генеральную совокупность (явление в целом). Оценка результатов исследования предусматривает вычисление:
· средней ошибки (ш) для средних (М) или относительных (Р) величин;
· доверительных границ средних (М) или относительных (Р) величин;
· достоверности разности средних (М) или относительных (Р) величин по критерию t.
Среднюю ошибку (m), которая является важнейшей статистической величиной, определяют по формулам:
§ для относительной величины (Р)
m%= 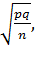
§ для средней величины (M) при n ≤ 30
mM= 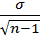 ,
,
§ для средней величины (M) при n ˃ 30
mM= 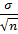 ,
,
где m – ошибка средней или относительной величины
P– показатель, выраженный в процентах (%), промилле (‰)) и т.д.
q – величина, равная 100 - P(при вычислений в процентах, т.е. когда
P выражен в процентах), 1000 – P (при вычислений в промиллях)
σ– среднееквадратическое отклонение;
n – число наблюдений.
Величина ошибки средней арифметической прямо пропорциональна степени разнообразия признака в статистической совокупности и обратно пропорциональна квадратному корню из числа наблюдений. Следовательно, уменьшение величины ошибки возможно за счет либо снижения степени разнообразия признака, либо увеличения числа наблюдений. Как правило, в медико-статистических исследованиях обычно используют доверительную вероятность (надежность), равную 95,5 - 99,7 %.
Таким образом, если среднее квадратическое отклонение (σ) характеризует степень разнообразия вариант в вариационном ряду и необходима для определения ошибки средней, то величина ошибки (m) вместе с доверительным коэффициентом (t) является важным условием определения доверительного интервала, с помощью которого оценивают доверительные границы изучаемого признака.
Например, при вычислении среднего пульса у 26 студентов перед экзаменом (М = 76,9 уд/мин) средняя ошибка составила:
m = 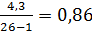
|
|
Это означает, что при аналогичных исследованиях при доверительной вероятности 68,3 % средняя величина пульса у студентов перед экзаменом может быть в пределах 76,9 ± 0,86, или от 76 до 78 уд/мин.
При более высокой степени доверительной вероятности (95,5 %, 99,7 % и др.) средняя величина будет иметь больший предел варьирования среднего результата, который определяется произведением "t • ш", где доверительный коэффициент (t) берется из соответствующей таблицы (табл.11).
| K = n-1 | Доверительная вероятность (P) | K= n-1 | Доверительная вероятность (P) | ||||
| 95,5% | 99,7% | 99,9% | 95,5% | 99,7% | 99,9% | ||
| 1 | 12,70 | 63,36 | 637,59 | 16 | 2,12 | 2,92 | 4,02 |
| 2 | 4,30 | 9,92 | 31,60 | 17 | 2,11 | 2,90 | 3,96 |
| 3 | 3,18 | 5,84 | 12,94 | 18 | 2,10 | 2,88 | 3,92 |
| 4 | 2,78 | 4,60 | 8,61 | 19 | 2,09 | 2,86 | 3,88 |
| 5 | 2,57 | 4,03 | 6,86 | 20 | 2,09 | 2,84 | 3,85 |
| 6 | 2,42 | 3,71 | 5,96 | 21 | 2,08 | 2,83 | 3,82 |
| 7 | 2,36 | 3,50 | 5,31 | 22 | 2,07 | 2,82 | 3,79 |
| 8 | 2,31 | 3,36 | 5,04 | 23 | 2,07 | 2,81 | 3,77 |
| 9 | 2,26 | 3,25 | 4,78 | 24 | 2,06 | 2,80 | 3,75 |
| 10 | 2,23 | 3,17 | 4,59 | 25 | 2,06 | 2,79 | 3,73 |
| 11 | 2,20 | 3,11 | 4,44 | 26 | 2,06 | 2,78 | 3,71 |
| 12 | 2,18 | 3,06 | 4,32 | 27 | 2,05 | 2,77 | 3,69 |
| 13 | 2,16 | 3,01 | 4,22 | 28 | 2,05 | 2,76 | 3,67 |
| 14 | 2,14 | 2,98 | 4,14 | 29 | 2,04 | 2,76 | 3,66 |
| 15 | 2,13 | 2,95 | 4,07 | 30 | 2,04 – 1,96 | 2,75 – 2,58 | 3,64 – 3,29 |
Таблица 11
Значение критерия Стьюдента (t)
При обследовании 26 студентов и доверительном коэффициенте t = 2,06 (табл. 12), если доверительная вероятность равна 95,5 %, средний пульс у студентов при аналогичных исследованиях составит 76,9 ± 2,06 • 0,86 уд/мин, или его величина будет в среднем от 75 до 79 уд/мин.
При большом числе наблюдений (п>30), как правило, доверительный коэффициент (t) берется равным 1 при Р = 68,3 %,2 — при Р = 95,5 % и 3 — при Р = 99,7 %. Так, при обследовании 212 студентов-мужчин 22 лет (см. табл. 7) и вычислении среднего роста (М = 176,74 см), средней ошибки (ш = 0,4 см) предел колеблемости средней при повторных аналогичных исследованиях при Р = 68,3 % составит 176—178 см (176,74 ± 0,4 см), а при Р = 95,5 % и t = 2 средний рост студентов-мужчин будет в пределах от 175 до 178 см (176,74 ±2-0,4 см).
Таким образом, при t= 1 вероятность приведенного предела колебаний средней величины (средний пульс, средний рост и т. д.) составит лишь 68,3 %, а 31,7 % полученных средних могут оказаться вне вычисленных пределов. При t= 2,06 или t= 2,0 вероятность получения средней в обозначенных пределах при проведении аналогичных исследований составит 95,5 % и лишь 4,5 % результатов окажется вне этих границ. Следовательно, с повышением доверительной вероятности увеличивается ширина доверительного интервала. Сравнение средних и относительных величин по критерию t .
На практике нередко для того, чтобы сделать вывод об эффективности предлагаемого нового метода лечения или диагностики, приходится сравнить результаты, полученные в исследуемой и контрольной группах. Целью сравнения двух средних (М) или относительных показателей (Р) являются оценка существенности их различий, установление их достоверности.
Достоверность разности между двумя средними и относительными величинами определяют по формулам:
для средних величинt = 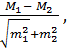
для относительных величин t = 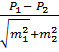
где M1и М2 - средние величины, полученные в двух самостоятельных независимых группах наблюдений (исследуемая и контрольная);
P1и Р2 - показатели изучаемого признака, выраженные в процентах;
m1иm2- средние ошибки средних или относительных величин;
t- доверительный коэффициент.
При t> 2 различие между двумя средними величинами существенно и не случайно, т. е. достоверно. Это значит, что в генеральной совокупности сравниваемые средние величины (или относительные величины) имеют различие и при повторении подобных наблюдений будут получены аналогичные различия. При t= 2 надежность такого вывода будет не меньше 95 %. С увеличением критерия достоверности (t) степень надежности различия между средними величинами (или относительными величинами) также повышается, а риск ошибки уменьшается. При t< 2 достоверность разности средних величин (или относительных величин) считается недоказанной.
Так, изучение содержания гормонов в крови показало, что уровень эстрадиола у мальчиков в возрасте 7-10 лет составил среди больных эпилепсией 23,5 ± 3,4 (45 детей), в контрольной группе 32,4 ± 2,3 (53 ребенка). Для определения достоверности различия средних необходимо использовать приведенную ранее формулу и провести следующие расчеты:
t = 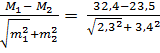 =
= 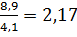
Полученные данные свидетельствуют о том, что различие между двумя средними существенны, достоверны, не случайны, статистически значимы, так как t= 2,17 и, следовательно, с достоверностью более 95,5 % можно утверждать о снижении содержания эстрадиола в крови 7—10-летних мальчиков, больных эпилепсией, в сравнении с этим показателем у детей в контрольной группе.
При анализе числа нейроэндокринных нарушений у детей, больных эпилепсией (115 человек), и в группе сравнения (92 человека) было отмечено, что нарушения пубертатного развития среди больных отмечаются в 27,4 %, а в контрольной группе — в 11,2 % случаев. Для определения достоверности различия между двумя показателями распространенности нарушений пубертатного развития сначала следует вычислить ошибки для каждого показателя по соответствующим формулам:
m1 = 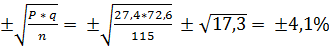 ,
,
m2 = 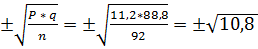 =
= 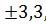
Далее производим вычисление по формуле:
t = 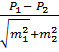 =
= 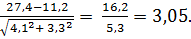
Полученные данные свидетельствуют о том, что имеющиеся различия в показателях существенны, достоверны, не случайны, статистически значимы, поэтому можно утверждать о большей распространенности нарушений пубертатного развития у детей, больных эпилепсией, по сравнению со здоровыми детьми. Если доверительный коэффициент t> 3, то с достоверностью более 99,7 % можно утверждать, что число нарушений пубертатного развития у детей с эпилепсией в 2,4 раза выше, чем у здоровых детей.
Дата: 2018-11-18, просмотров: 491.