Зная величи­ну ошибки, можно рассчитать необходимый объем наблюдений для проведения выборочного исследования и получения досто­верных результатов. Поскольку искомые закономерности мож­но выявить, исследовав только генеральную совокупность, не следует забывать, что проведение выборочных исследований требует существенно меньше средств. Однако получение дос­товерных результатов возможно лишь в том случае, если выбо­рочная совокупность является репрезентативной, т. е. предста­вительной по отношению к генеральной совокупности по ко­личеству и по качеству. Научной основой выборочного метода является закон больших чисел и теория вероятности, которые позволяют сформулировать следующие основные положения закона больших чисел:

·  при увеличении числа наблюдений данные выборочной совокупности стремятся воспроизвести данные генераль­ной совокупности;

·  при достижении определенного, достаточного количества данные выборочной совокупности воспроизводят данные генеральной совокупности.

Статистические методы позволяют обрабатывать любое чис­ло наблюдений (как было показано ранее), но чтобы застрахо­вать себя от получения недостоверного результата, следует зара­нее определить необходимый объем наблюдений для получения достоверных результатов. С этой целью используют специаль­ные формулы, полученные при помощи преобразования фор­мул предельных ошибок для средних и относительных величин:

tm_абс. = t 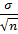,                              tm_%= t ,

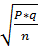где n— число наблюдении,

t— доверительный коэффициент,

а — среднее квадратическое отклонение,

р — результирующий признак, выраженный в процентах,

q— величина, равная 100 — р,

tm= ∆ — предельно допустимая максимальная ошибка с дос­таточной степенью вероятности.

Решая приведенные равенства путем алгебраических преоб­разований относительно "п", получают формулы для определе­ния числа наблюдений, когда выбранный признак берется:

· в абсолютных цифрах    n = ,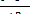

· в относительных величинах n =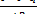

Приведенные формулы для случайного повторного отбора определяют оптимальный объем выборки для исследования су­ществующих закономерностей и получения достоверных ре­зультатов. Необходимо лишь выбрать признак или признаки для проведения соответствующих вычислений, что в ряде слу­чаев затруднено, поскольку единицы наблюдения в исследуемых совокупностях характеризуются множеством учетных призна­ков. Так, в комплексных социально-гигиенических исследова­ниях изучают не только комплекс показателей, свидетельствую­щих о состоянии здоровья изучаемой группы населения, но и окружающие условия, факторы, воздействующие на здоровье. Вести расчет по всем исследуемым признакам невозможно, по­этому, как правило, выделяют 2—3 результирующих признака и конкретно по ним рассчитывают необходимый объем наблю­дений.

Сведения о критериях, характеризующих разнообразие при­знаков (σ и Р) и нужных для расчета необходимого числа на­блюдений, получают:

·  из данных литературы;

·  если признак выражен абсолютным числом и в литерату­ре данных о нем нет, то используют результаты пробного исследования, объем которого обычно составляет не ме­нее 30 единиц наблюдения;

·  если признак выражен относительным числом, то берут значение максимального произведения pq= 2500 (р = q=  50 %) или pq= 0,25 (р = q= 0,5), так как не следует пробное исследование проводить и вычислять проценты при числе наблюдений менее 100.

Степень доверительной вероятности при вычислении необ­ходимого объема наблюдений зависит от целей и задач иссле­дования, но обычно составляет не менее 95,5 % (или 0,95), при которой t= 2. Величина максимальной ошибки (∆) выражается в единицах изучаемого признака, характеризует допускаемую неточность искомой величины в сравнении с генеральной со­вокупностью, задается в разумных пределах в зависимости от целей и задач исследования. Незначительное увеличение ∆ ве­дет к резкому сокращению необходимого объема выборки, на­против, незначительное уменьшение ∆ резко его увеличивает.

Например, для изучения состояния здоровья детей первых 3 лет жизни в связи с особенностями состояния здоровья роди­телей необходимо рассчитать среднее квадратическое отклоне­ние, равное 1,6; число наблюдений для получения достоверного результата. В качестве результирующего признака была взята кратность перенесенных детьми заболеваний на 2-м году жизни. Индивидуальная характеристика заболеваемости детей ранее не изучалась. При проведении пробного исследования, включающего обследование 28 детей 2-го года жизни, были получены следующие данные:

М - среднее число перенесенных ребенком заболеваний в год составило 3,8;

 σ — предельно допустимая ошибка, равная 0,2;

р - доверительная вероятность, равная 95,5 %;

t - доверительный коэффициент, равный 2.

Расчет производят по формуле:n = 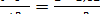 = 256 единиц наблюдения

Вывод: для получения статистически достоверных данных о состоянии здоровья детей первых 3 лет жизни в связи с особен­ностями здоровья их родителей необходимо обследовать 256 детей.

В качестве другого результирующего признака был взят по­казатель "индекс здоровья", отражающий удельный вес детей, не болевших на 1-м году жизни. При анализе данных литера­туры было установлено, что среди детей количество не болев­ших на 1-м году жизни в Москве составило 9,5 %. При довери­тельной вероятности 95,5 % и предельно допустимой ошибке 3,5 % необходимое число наблюдений было определено по формуле и составило 280,7:

n = 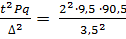 = 280,7 единиц наблюдения

где р -  результирующий признак, выраженный в процентах и равный 9,5 %;

q-  величина, равная 100 — р и составившая 90,5 %;

∆ - предельно допустимая ошибка, равная 3,5 %;

Р - доверительная вероятность, равная 95,5 %;

t- доверительный коэффициент, равный 2.

Вывод: для получения статистически достоверных данных о состоянии здоровья детей необходимо обследовать 281 ребенка в возрасте от 0 до 3 лет.

Учитывая результаты определения необходимого объема на­блюдений для получения статистически достоверных данных о состоянии здоровья детей первых 3 лет жизни на основании произведенных расчетов по двум результирующим признакам (в первом случае 256 единиц наблюдения, а во втором - 281), необходимо обследовать не менее 282 детей данного возраста.

Иногда при определении основного (результирующего) при­знака и его предельно допустимой ошибки, особенно при изу­чении совсем незнакомых совокупностей, возникают трудно­сти, которых можно избежать, если воспользоваться данными табл.12, где значения ∆ и σ не определяют заранее, а беруториентировочное соотношение ∆ и σ (∆/σ). Последнее обозна­чают как коэффициент точности (К), уровень соотношения вы­бирают в зависимости от цели и задач исследования в пределах от 0,5 до 0,1.

Как следует из табл.12, необходимый объем выборки для получения устойчивых результатов с достаточной степенью уве­ренности и точности составляет 400 единиц наблюдения при точности исследования (К) 0,1 и доверительной вероятности (Р) 95,4 %, что несколько выше, чем при проведении расчетов.

                                                                                                       Таблица 12

Необходимый объем выборки в зависимости от точности исследования и доверительной вероятности

Вид исследования