Разнообразие признака характеризует третье свойство статистической совокупности, которое проявляется в том, что в однородных статистических совокупностях величины количественных признаков различны. Например, при измерении окружности головы 2-летних детей в трех группах были получены данные, представленные в табл. 8.
Таблица 8
Окружность голову у детей 2-летнего возраста в трех группах
| Показатель | 1-я группа ( n = 42) | 2-я группа ( n = 42) | 3-я группа ( n = 42) |
| Окружность головы ( V) , см. Число детей ( p) | 46 44 45 46 47 48 42 43 44 45 46 47 48 49 50 42 1 8 25 6 2 1 2 4 6 14 10 3 - 2 | ||
В каждой из сравниваемых групп было одно и то же число наблюдений, равное 42, одна и та же средняя взвешенная (окружность головы), составившая 46 см, но группы были различны по составляющим их вариантам. Если в 1-й группе все дети имели окружность головы 46 см, то во 2-ю группу вошли дети с окружностью головы от 44 до 48 см, а в 3-ю — от 42 до 50 см. В этом проявляется разнообразие, колеблемость признака изучаемой совокупности.
Наибольшее разнообразие признака (окружность головы) представлено в 3-й группе, в которую вошли дети с наименьшими и наибольшими размерами окружности головы. Статистическими критериями, характеризующими разнообразие признака, являются:
· лимит (lim);
· амплитуда (Аm);
· среднее квадратическое отклонение (σ);
· коэффициент вариации (С v ).
Лимит(lim) определяется крайними значениями вариант в вариационном ряду (Vmax- Vmin) и составляет для 2-й группы lim2= от 44до48 см, для 3-й группы lim3 = от 42 до 50 см.
Амплитуда (Аm) равна разности между крайними вариантами (Vmax-Vmin). Для 2-й группы амплитуда составила Аm2 = 4 см, для 3-й - Аm3 = 8 см.
И лимит, и амплитуда свидетельствуют о большем разнообразии признака в 3-й группе (с учетом лишь крайних значений вариант вариационного ряда).
Наиболее полную характеристику разнообразию вариационного ряда дает среднее квадратическое отклонение (σ), которое учитывает разнообразие всех вариант вариационного ряда. Существует два способа расчета этого показателя. Один из них простой и называется среднеарифметическим, для чего используют формулу:
σ = 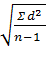 ,
,
где σ - среднее квадратическое отклонение;
d- разница между вариантой и средней арифметической (V - М);
п - число наблюдений.
Этот способ вычисления среднего квадратического отклонения применяют, если число наблюдений не превышает 30 (п< 30), каждая варианта встречается 1 раз (Р = 1), то среднюю величину вычисляют как простую среднюю арифметическую. В том случае, если варианты имеют различную частоту больше 1, то вычисляют среднее, взвешенное квадратическое отклонение и применяют формулу:
σ = 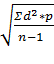 ,
,
где σ — среднее квадратическое отклонение;
d— разница между вариантой и средней арифметической (V - М);
п — число наблюдений;
р — частота, с которой встречается каждая варианта.
В качестве примера вычисления средней и среднего квадратического отклонения при числе наблюдений п< 30 приведем определение пульса у студентов перед сдачей экзамена (табл. 9).
Таблица 9
Определение среднего квадратического отклонения среднего пульса у студентов-мужчин 20-22 лет перед сдачей экзамена
| Пульс у студентов-мужчин ( V ) | Число студентов (p) | 
| d = (V – M) | d 2 | d2 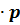
|
| 68 69 72 76 77 79 80 84 86 | 1 1 4 5 4 7 1 2 1 𝞢p = n = 26 | 68
69
288
380
308
553
80
168
86 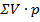 = 2000 = 2000
| -8,9 -7,9 -4,9 -0,9 0 +2,1 +3,1 +7,1 +9,1 | 79,21 62,41 24,01 0,81 0 4,41 9,61 50,41 82,81 | 79,21
62,41
96.04
0,81
0
30,87
9,61
100.82
82,81
𝞢 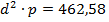
|
Для вычисления среднего квадратического отклонения необходимо рассчитать отклонение каждой варианты от средней, возвести в квадрат, умножить на частоту встречаемости данной варианты, суммировать произведение и подставить в формулу:
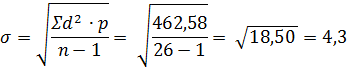
Таким образом, среднее квадратическое отклонение (σ) при обследовании 26 студентов (n = 26) и средней величине пульса (M) 76,9 уд/мин. соответствовал 4,3.
В том случае, если число наблюдений превышает 30 и среднюю величину рассчитывают по способу моментов, то и среднее квадратическое отклонение вычисляют по способу моментов по формуле:
σ = 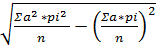
где 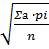 - первый момент средней,
- первый момент средней,

а - разница между вариантой и условно средней,
р - частота, с которой встречается каждая варианта,
i -величина интервала,
п - число наблюдений.
Для вычисления среднего квадратического отклонения в таблицу вычисления средней по способу моментов необходимо включить еще одну графу (табл. 10).
Среднее квадратическое отклонение при обследовании (n) 212 студентов и M = 176,74 см. составило:
σ = 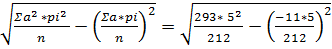 =
= 
По величине среднего квадратического отклонения можно судить о разнообразии вариационного ряда: чем больше величина σ, тем больше разнообразие, чем меньше значение σ тем меньше разнообразие вариант и тем более однороден вариационный ряд.
Таблица 10
Определение среднего роста студентов-мужчин 20-22 лет
| Рост студентов-мужчин ( V ), см. | Центральная варианта группы ( 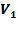 ) )
| Число студентов (p) | 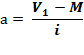
| а  p p
| 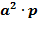
|
| 160-164 165-169 170174 175-179 180-184 185-189 | 162 167 172 177 182 187 | 4 21 47 68 54 18 𝞢p = n = 212 | -3 -2 -1 0 +1 +2 | -12
-42
-47
0
+54
+36
𝞢а  p = -11 p = -11
| 36
84
47
0
54
72
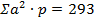
|
Среднее квадратическое отклонение связано со структурой распределения.
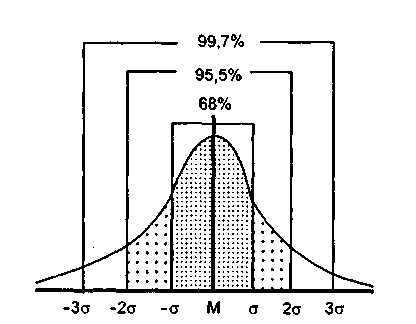
При нормальном распределении в пределах М ± σ находится 68,3 %, М ± 2σ - 95,5 %, М ± Зσ- 99,7 % всех вариант (рис.3).
|
Рис. Связь среднего квадратического отклонения со структурой вариационного ряда. |
Иными словами, если 95 % всех вариант вариационного ряда находится в пределах М ± 2а, то средняя величина характерна для данного ряда и можно говорить о ее представительности для статистической совокупности и не требуется увеличивать число наблюдений. Практическое значение среднего квадратического отклонение состоит в том, что по его величине можно:
· определить структуру вариационного ряда;
· охарактеризовать степень однородности вариационного ряда в
· зависимости от величины а;
· судить о типичности средней арифметической в зависимости от
· распределения вариант в вариационном ряду;
· оценить отдельные признаки у каждого индивидуума по стандартному отклонению от средней арифметической по формуле:
t= 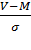 ,
,
где t – доверительный интервал,
М – средняя величина;
· определить коэффициент вариации при сравнении степени разнообразия разных признаков в одной совокупности или однородных признаков в разных совокупностях;
· определить достоверность (репрезентативность) результатов исследования.
Коэффициент вариации (Cv) является относительной мерой разнообразия, так как вычисляется по отношению среднего квадратического отклонения (σ) к средней арифметической величине (М), выраженному в процентах (100 %):
Cv 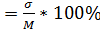
Коэффициент вариации применяют в том случае, когда необходимо сравнить разнообразие разных признаков в одной совокупности (разные показатели крови) или одного признака в разных совокупностях (масса тела у младенцев и подростков). Для ориентировочной оценки степени разнообразия признака пользуются следующими градациями коэффициента вариации. При величине коэффициента вариации (Сv) больше 20 % отмечают сильное разнообразие, если CVот 20 до 10 %, то разнообразие среднее, а если Cvменьше 10 %, то разнообразие слабое.
Дата: 2018-11-18, просмотров: 474.