Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Статистическая совокупность как группа изучаемых явлений обладает особыми групповыми свойствами. Эти свойства присущи только статистической совокупности (табл. 4).

   Таблица 4

Основные групповые свойства и статистические критерии совокупности

 

Групповые свойства	Статистические критерии
Распределение признака	Частота, доля (%, ‰, относительные величины)
Средний уровень признака	Мо – мода, Ме– медиана М – средняя арифметическая величина
Разнообразие признака	Lim – лимит; Am – амплитуда σ – среднее квадратическое отклонение
Репрезентативность признака	mM – средняя ошибка средней арифметической m% - средняя ошибка относительной величины (%) χ2 – коэффициент соответствия (хи – квадрат)
Взаимосвязь между признаками	rxy – коэффициент корреляции

 

К основным групповым свойствам статистической совокупности относятся следующие: распределение признака, его средний уровень, разнообразие и репрезентативность, взаимосвязь между признаками.

Распределение признака – это одно из важных свойств совокупности; оно заключается в том, что элементы совокупности распределяются неодинаково, по величине признака, образуя определенную внутреннюю структуру группы. Анализ структуры позволяет вскрыть важнейшие закономерности, присущие тому или иному явлению.

Средний уровень признака как свойство совокупности дает обобщенную характеристику различным величинам количественного признака, выразив его одним числом.

Средним уровнем характеризуют количественные признаки, т.е. признаки, имеющие числовые значения (рост, масса и др.).

Разнообразие признака указывает, что группа состоит из объектов, различных по величине изучаемого признака.

Репрезентативность признака (представительность, типичность) означает способность выборочных совокупностей отражать свойства генеральных совокупностей. Для измерения этого свойства используются ошибки репрезентативности (m).

Ошибки репрезентативности показывают, насколько результаты выборочного исследования отличаются от результатов, которые могли бы быть получены при сплошном изучении генеральной совокупности.

Взаимосвязь между признаками – это степень зависимости размеров признаков друг от друга.

1.4.1. Первое свойство статистической совокупности - распределение признака в статистической совокупности

Основными величинами, которыми оперирует статистика, яв­ляются абсолютные и относительные величины, отражающие качественную структуру статистической совокупности и харак­теризующие распределение признаков (первое свойство стати­стической совокупности).

Абсолютные величины используют очень широко. Они нуж­ны для общей характеристики явления, признака: например, это численность населения в мире, в конкретной стране, в го­роде, районе и т. д.; при учете редких инфекционных заболе­ваний (малярия, полиомиелит и др.); число врачей, учреждений здравоохранения, коек и пр.

Однако при сравнении данных возникает необходимость применения относительных величин (или показателей), которые получают при соотношении, сопоставлении двух сравниваемых чисел. Типы распределения признаков в статистической сово­купности представлены на рис. 3.

 

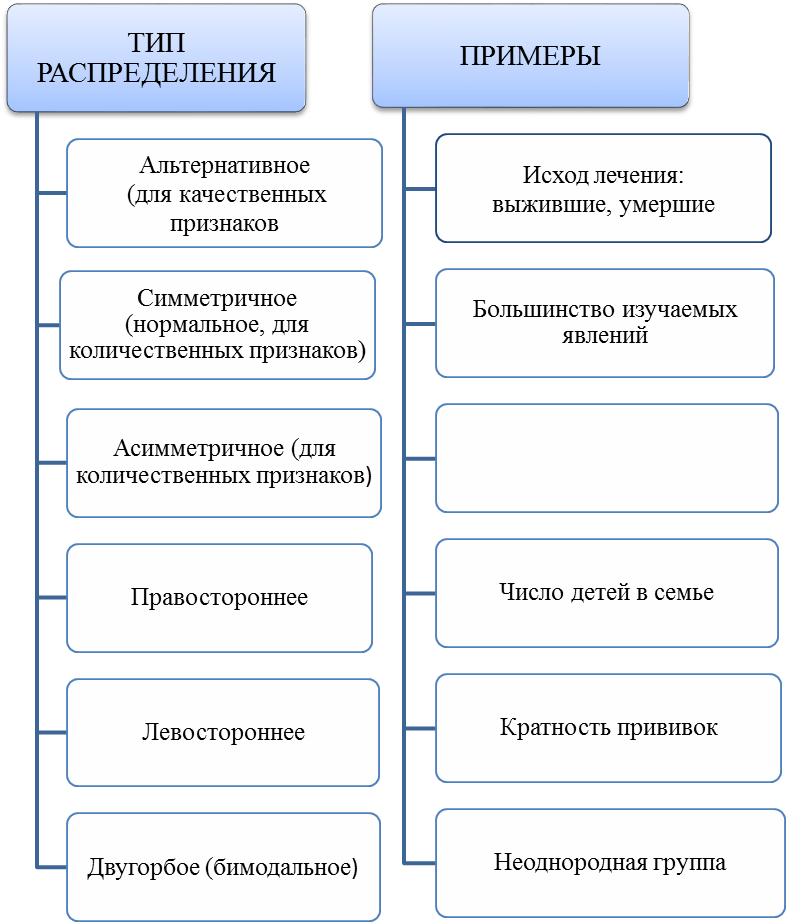
Рис. 3.  Типы распределения признаков в статистической совокупности

 

В целом относительные величины, характеризующие рас­пределение признаков и применяемые в медицине, представ­лены следующими показателями:

•  экстенсивные показатели

•  интенсивные показатели

•  показатели соотношения

• показатель наглядности

•  показатели динамического ряда.

Для удобства сопоставления, обычно перечисленные показа­тели вычисляют на 100, 1000, 10 000, 100 000, для чего умножа­ют на круглое число (100, 1000, 10 000, 100 000 и т. д.), назы­ваемое основанием. В результате полученные коэффициенты приобретают форму "процентов" (%), "промилле" (‰), "продецимилле" (‰_о) и т. д. Чем реже встречается изучаемое явление, тем больше числовое основание следует выбрать, чтобы не было коэффициентов меньше единицы, которыми неудобно пользо­ваться. Принято, например, структуру какого-то явления выра­жать в процентах, а демографические показатели (рождаемость, смертность) — в промилле; распространенность заболеваний — на 100000 населения.

Экстенсивные показатели (коэффициенты) характеризуют распределение явления на его составные части, определяют его внутреннюю структуру, удельный вес части в целом, долю при­знака в статистической совокупности. При вычислении экстен­сивных показателей используют только одну статистическую совокупность и ее состав. Большинство экстенсивных показа­телей определяют в процентах (%), реже в промилле (%>) и до­лях единицы. Вычисление осуществляют по формуле:

Экстенсивный показатель = *100%

Например, в прошедшем году среди учащихся 1-го класса было зарегистрировано 387 случаев заболеваний желудочно- кишечного тракта, в том числе 224 случая заболеваний гастри­том. Удельный вес лиц, страдающих гастритом, составил 57,9 % .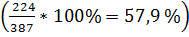

В качестве примеров экстенсивных показателей, используе­мых в здравоохранении, можно назвать структуру заболеваемо­сти, смертности, инвалидности и т. д. Следует помнить, что экстенсивными показателями следует пользоваться в тех случа­ях, когда необходимо охарактеризовать статистическую сово­купность в данном месте и в данное время. Для сравнения по­казателей в динамике коэффициенты экстенсивности непри­годны. Для этой цели нужно знать численность среды, в которой происходит явление, и пользоваться интенсивными показателями.

Интенсивные показатели (коэффициенты) характеризуют частоту (интенсивность, уровень, распространенность) явления за определенный промежуток времени (чаще за год) в среде, в которой это явление происходит и с которой оно непосредст­венно связано. При вычислении интенсивных показателей не­обходимо знание двух статистических совокупностей, одна из которых представляет среду, другая — явление. В демографи­ческой и санитарной статистике в качестве среды чаще всего рассматривают население и в расчете на него вычисляют то или иное явление, например число рождений, число заболеваний, общее число смертей за год на определенную численность на­селения. Показатель интенсивности рассчитывают на 100, 1000, 10 000 или 100 000) по формуле:

Интенсивный показатель =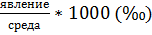

Типичными интенсивными показателями являются демо­графические показатели и коэффициенты заболеваемости, вы­числяемые для населения в целом или для отдельных опреде­ленных групп людей, например, в одном из регионов страны за год родились живыми 3000 детей, в течение 1-го года умерли 52ребенка. Показатель младенческой смертности составил 17,3 ‰ ( ).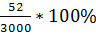

Показатели соотношения (коэффициенты) характеризуют частоту встречаемости признака в статистической совокупности, его распространенность и применяются при сравнении двух, не связанных между собой статистических совокупностей, но со­поставимых логически и по содержанию. К ним относят такие показатели, как число врачей, число больничных коек на 1000 населения, количество различных исследований, перели­ваний крови на 100 (или 1000) больных. По методике вычисле­ния показатели соотношения схожи с показателями интенсив­ности, но различны по содержанию.

Динамический ряд — это совокупность однородных стати­стических величин, показывающих изменение какого-либо яв­ления (признака) во времени. Числа, из которых составляется динамический ряд, могут быть представлены абсолютными, средними и относительными величинами. Если динамический ряд состоит из абсолютных величин, то он называется простым, если он составлен из средних или относительных чисел, то та­кой динамический ряд называется сложным или производным.

Динамические ряды бывают двух видов:

• моментными, состоящими из величин, характеризующих явление на определенный момент времени (на конец го­да, месяца, декады и т. д.);

• интервальными, состоящими из величин, которые харак­теризуют явление за определенный промежуток (интер­вал) времени (за год, месяц и т. п.).

С целью изучения особенностей изучаемого процесса и дос­тижения наглядности в характеристике рассматриваемого явле­ния рассчитывают специальные показатели динамического ря­да, среди которых следует назвать абсолютный прирост, темп прироста (убыли), показатель роста (снижение), показатель на­глядности (табл. 3.6).

Абсолютный прирост представляет собой разность между по­следующим и предыдущим уровнем. Он измеряется в тех же единицах, что и уровни динамического ряда.

Темп прироста (убыли) показывает отношение абсолютного прироста (снижения) каждого последующего уровня к пре

Динамический ряд, как правило, позволяет проследить ос­новную закономерность явления, проявляющуюся в последо­вательном снижении или увеличении показателей динамиче­ского ряда.

Анализ динамического ряда включает в себя вычисление ряда показателей, при необходимости проведение выравнивания и графическое изображение.

1.4.2. Второе свойство статистической совокупности — средний уровень признака в статистической совокупности

В медицине и здравоохранении при анализе, кроме распреде­ления, довольно часто используют средние величины, характе­ризующие физическое развитие пациентов (рост, масса тела, окружность груди и т. д.), данные их обследования (частота ды­хания и пульса, артериальное, внутриглазное и внутричерепное давление и т. д.), результаты анализов (содержание гемоглоби­на, число эритроцитов, лейкоцитов, СОЭ) и др. В каждой со­вокупности и в данных конкретных условиях один и 'тот же признак отличается от величины этого же признака в другой со­вокупности, при наличии других условий. Так, величина пуль­са, артериального давления, температуры тела, длительность временной нетрудоспособности и другие критерии отличаются (варьируют) даже у больных с одним диагнозом. Иными слова­ми, признаки могут принимать различные числовые значения у разных единиц совокупности, при этом нередко могут повто­ряться у нескольких единиц наблюдения.

Полученные при исследовании одного и того же признака у единиц наблюдения статистической совокупности абсолютные величины сначала записывают в том порядке, как их получает исследователь, т. е. хаотично.

 Каждое числовое значение изу­чаемого признака называется вариантой (V), а числа, показы­вающие, как часто повторяются одни и те же варианты, назы­вают частотой (Р).

Ряд вариант одного и того же признака, рас­положенных в определенном порядке (по степени возрастания или убывания), с соответствующими им частотами, образуют вариационный ряд.

Вариационные ряды бывают простые или несгруппированные, которые составляют, как правило, при ма­лом числе наблюдений (до 30 единиц наблюдения), и сгруппи­рованные, которые составляют при большом числе наблюдений (более 30 единиц наблюдения).

Обобщенной характеристикой вариационного ряда являются средние величины, положительные качества которых заключаются в том, что они характеризуют большую совокупность однородных явлений.

Различают несколько видов средних величин:«Мода, медиана, средняя арифметическая, средняя геометрическая,средняя гармоническая и т. д.

Модой (Мо) называется варианта, встречающаяся с наиболь­шей частотой.

Медианой(Me) — варианта, которая делит вариа­ционный ряд пополам и расположена в середине вариационно­го ряда, если ряд нечетный, и если ряд четный, то определяется как полусумма двух средних вариант.

Наиболее часто в характеристике вариационного ряда ис­пользуют среднюю арифметическую. Средняя арифметическая, которая рассчитана в вариационном ряду, где каждая варианта встречается только 1 раз, называется средней арифметической простой. Ее определяют по формуле:

 

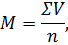
где М — средняя арифметическая,

V — варианта изучаемого признака,

п — число наблюдений.

Если в исследуемом ряду одна или несколько вариант по­вторяются несколько раз, то вычисляют среднюю арифметиче­скую взвешенную, когда учитывается вес каждой варианты в за­висимости от частоты ее встречаемости. Расчет такой средней проводят по формуле:M =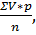

где М - средняя арифметическая взвешенная,

V -  варианты (числовые значения изучаемого признака), р — частота, с которой встречается одна и та же варианта признака, т. е. сумма вариант с данным значением признака,

п - число наблюдений, т. е. сумма всех частот или общее число всех вариант (𝞢р).

Например, при определении среднего пульса у студентов пе­ред экзаменом следует сначала вычислить 𝞢V• р, а за­тем среднюю величину, которая составила М = 76,9 уд/мин (2000/26) (табл. 5).

                                                                                                              Таблица 5

Определение среднего пульса у студентов-мужчин 20-22 лет

 

Пульс у студентов-мужчин (V)	Число студентов (p)
68 69 72 76 77 79 80 84 86	1 1 4 5 4 7 1 2 1 𝞢p = n = 26	68 69 288 380 308 553 80 168 86  = 2000

 

Нередко при большом числе наблюдений для вычисления средней арифметической взвешенной используют сгруппиро­ванный вариационный (или разбитый на равные интервалы) ряд. Такой вариационный ряд должен быть непрерывным, ва­рианты, расположенные в определенном порядке (возрастания или убывания), следуют друг за другом (табл. 6).

При группировке вариационного ряда следует учитывать, что интервал выбирает исследователь, величина интервала зависит от цели и задач исследования.

Число групп в сгруппированном вариационном ряду определяют в зависимости от числа наблюдений. При числе наблюдений от 31 до 100 рекомендуется иметь 5-6 групп, от 101 до 300 - от 6 до 8 групп, от 301 до 1000 наблюдений можно использовать от 10 до 15 групп. Расчет интервала (i) производится по формуле (округление в сторону увеличения): 

i =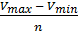

где i - величина интервала,

Vmax - максимальное значение варианты,

Vmin - минимальное значение варианты.

                                                                                                          Таблица 6

Определение среднего роста студентов-мужчин 20-22 лет

Рост студентов-мужчин (V), см.	Центральная варианта группы ( 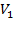)	Число студентов (p)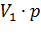
160-164 165-169 170174 175-179 180-184 185-189	162 167 172 177 182 187	4 21 47 68 54 18   𝞢p = n = 212	648 3507 8084 12036 9828 3366

 

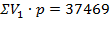
Расчет средней взвешенной в сгруппированном (или интервальном) ряду требует определения середины интервала, которую вычисляют как полусумму крайних значений группы.

Пример составления сгруппированного вариационного ряда представлен в табл. 6, а расчет средней величины производят по формуле:

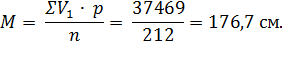
Однако при большом числе наблюдений, достаточно протяженном вариационном ряду рекомендуется среднюю взвешенную вычислять по способу моментов (табл. 7).

 

                                                                                                          Таблица 7

Определение среднего роста студентов-мужчин 20-22 лет

Рост студентов-мужчин (V), см.	Центральная варианта группы ( 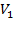)	Число студентов (p)		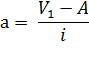а p
160-164 165-169 170174 175-179 180-184 185-189	162 167 172 177 182 187	4 21 47 68 54 18   𝞢p = n = 212	-3 -2 -1 0 +1 +2	-12 -42 -47 0 +54 +36 𝞢а p = -11

 

Этот способ основан на том, что средняя равна любой произвольно (условно) взятой средней (M₁) за которую чаще всего принимается мода (Мо), плюс среднее отклонение всех вариант от условно средней (первый момент средней):

 ,

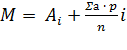где М - средняя арифметическая (взвешенная),

 А₁ - условно взятая средняя величина (наиболее чаще встречающееся величина),

i- величина интервала,

 а - отклонение между центральными вариантами групп и условной средней

величиной, выраженное в интервалах ,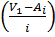

р - частота (число раз, с которым встречается одна и та же варианта признака),

п — число наблюдений, т. е. сумма всех частот или об­щее число всех вариант (𝞢р);

 

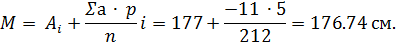
Таким образом, средняя взвешенная, вычисленная по спо­собу моментов, составила 176,74 см, что практически совпало с расчетами средней обычным методом - 176,7 см. Однако при вычислении средней по способу моментов используют простые цифры, вычисления менее громоздки, что значительно облег­чает и ускоряет расчеты.

Средняя арифметическая (средняя взвешенная) имеет ряд свойств, которые используют в некоторых случаях для упроще­ния расчета средней и получения ориентировочной величины.

1. Средняя арифметическая занимает срединное положение в строго

симметричном вариационном ряду (М = Mo= Me).

2. Средняя арифметическая имеет абстрактный характер и является

обобщающей величиной, выявляющей закономерность.

3.  Алгебраическая сумма отклонений всех вариант от сред­ней равна нулю.

 На этом свойстве основан расчет средней по способу моментов.

4.  Если к каждой варианте вариационного ряда прибавить или отнять одно

и то же число, то на столько же увеличится или уменьшится средняя

 арифметическая величина.

5.  Если каждую варианту разделить или умножить на одно и то же число,

 то во столько же раз уменьшится или увеличится средняя

арифметическая.

Два последних свойства используют в тех случаях, когда ва­рианты представлены очень малыми или наоборот большими числами.

В медицине и здравоохранении средними величинами оценивают отдельные показатели (параметры физического раз­вития), сравнивая данные лабораторных и других исследований с нормой. Следует учитывать, что средние рассчитывают на большой однородной группе, поскольку нарушение этого принципа приводит к искажению реальных процессов.

Графическое изображение вариационного ряда может быть представлено в виде графиков симметричного  асимметрич­ного распределения  в зависимости от числа на­блюдений и изучаемого признака.