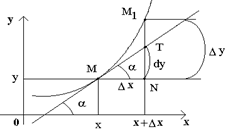
Рассмотрим функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол, который касательная образует с положительным направлением оси Ox. Дадим независимой переменной x приращение Δx, тогда функция получит приращение Δy = NM1. Значениям x+Δx и y+Δy на кривой y = f(x) будет соответствовать точка
M1(x+Δx; y+Δy).
Из ΔMNT находим NT=MN·tg α. Т.к. tg α = f '(x), а MN = Δx, то NT = f '(x)·Δx. Но по определению дифференциала dy=f '(x)·Δx, поэтому dy = NT.
Таким образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен приращению ординаты касательной к кривой y=f(x) в данной точке х.
Основные теоремы дифференциального исчисления. Раскрытие неопределенностей по правилу Лопиталя.
Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции (dy=f'(x)dx) и соответствующие теоремы о производных.
Например, так как производная функции у=с равна нулю, то дифференциал постоянной величины равен нулю: dy=с'dx=0•dx=0.
Теорема.1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:
Докажем, например, вторую формулу. По определению дифференциала имеем:
d(uv)=(uv)'dx=(uv'+vu')dx=vu'dx+uv'dx=udv+vdu
Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Пусть у=ƒ(u) и u=φ(х) две дифференцируемые функции, образующие сложную функцию у=ƒ(φ(х)). По теореме о производной сложной функции можно написать
у'х=у'u•u'x.
Умножив обе части этого равенства на dx, поучаем у'хdx=у'u•u'хdx. Но у'хdx=dy и u'хdx=du. Следовательно, последнее равенство можно переписать так:
dy=у'udu.
Сравнивая формулы dy=у'х•dx и dy=у'u•du, видим, что первый дифференциал функции у=ƒ(х) определяется одной и той же формулой независимо от того, является ли ее аргумент независимой переменной или является функцией другого аргумента.
Это свойство дифференциала называют инвариантностью (неизменностью) формы первого дифференциала.
Формула dy=у'х•dx по внешнему виду совпадает с формулой dy=у'u•du, но между ними есть принципиальное отличие: в первой формуле х — независимая переменная, следовательно, dx=∆х, во второй формуле и есть функция от х, поэтому, вообще говоря, du≠∆u.
С помощью определения дифференциала и основных теорем о дифференциалах легко преобразовать таблицу производных в таблицу дифференциалов.
Например: d(cosu)=(cosu)'udu=-sinu•du
Таблица дифференциалов



Теорема (правило Лопиталя). Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 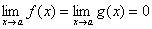 или
или 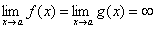 . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций 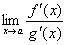 , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
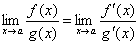 (1)
(1)
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например, найти 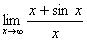 . Этот предел существует
. Этот предел существует 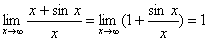 . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
. Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.
Примеры.
1. 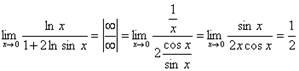 .
.
2. 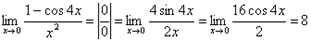 .
.
3. 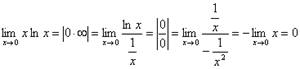 .
.
Дата: 2019-12-22, просмотров: 371.