Частным приращением функции z = 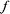(х, у) по х называется разность 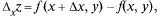частным приращением по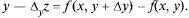

О: Частной производной по х от функции z = 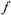(x, у) называется предел отношения частного приращения 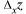к приращению Ах при стремлении последнего к нулю: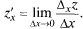

Другие обозначения: 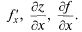Аналогично и для перемен-

ной у.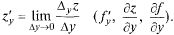

Заметив, что 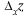определяется при неизменном у, а 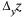— при неизменном х, можно сформулировать правило: частная производная по х от функции z = 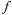(х, у) есть обычная производная по х, вычисленная в предположении, что у = const. Аналогично для вычисления частной производной по у надо считать х = const. Таким образом, правила вычисления частных производных те же, что и в случае функции одной переменной.

Примеры:

1)

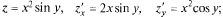
2)

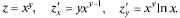
Частные производные функции нескольких переменных 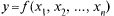определяются аналогично:

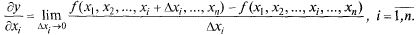
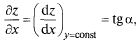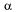Из геометрического смысла производной функции одной переменной имеем где — угол наклона касательной к 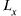в т. М(х, у, z) к оси ОХ. Аналогично для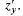

Пример: Найти угловые коэффициенты касательных к 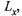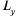поверхности 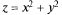в т. А(2, 3).

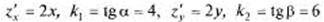
олным приращением функции z = 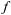(х, у) называется разность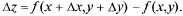

Замечание. В общем случае 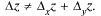Пусть, например,

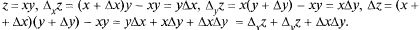
Аналогично полное приращение функции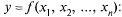

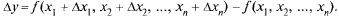
О: Функция z = 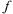(х, у) называется дифференцируемой в т. М(х, у), если ее полное приращение 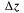представимо в виде 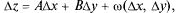где А, В не зависят от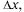

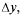а функция 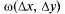является бесконечно малой более высокого порядка малости по сравнению с

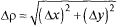при 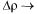0. Полным дифференциалом дифференцируемой функции в т. М(х, у) называется

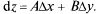
Докажем необходимое условие дифференцируемости функции. Т: Если функция z = 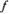(х, у) дифференцируема в т. М(х, у), то в этой точке существуют частные производные по х и y.

причем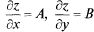

Выразим A и В через z = 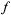(х, у). Пусть 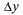= 0, тогда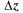 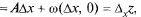т.е.

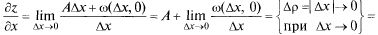
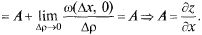
Аналогично

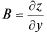
Поэтому

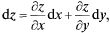
где обозначены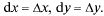

Можно показать, что обратное утверждение в общем случае неверно. Однако имеет место следующая теорема (достаточные условия дифференцируемости функции):

Т: Если частные производные 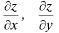непрерывны в т. М(х,у),

то функция z = 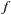(х, у) дифференцируема в этой точке Аналогично для функции 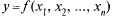вводится понятие дифференцируемости и полного дифференциала

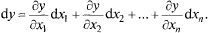
Пример: Найт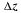и и 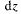для функции z - ху в т. М(2, 3) при 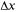= 0,1; 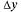=0,2.

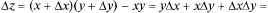
= 3 · 0,1 +2·0,2 + 0,1 · 0,2 = 0,72;

= 3 · 0,1 + 2 · 0,2 = 0,7

Пусть функция z = 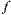(х, у) дифференцируема в т.(х, у). Найдем

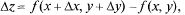откуда и 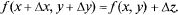Поскольку можно считать при малых 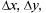что 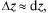то верно

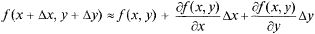(11.1)

с точностью до б.м. высшего порядка малости относительно Ах и 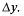Формулой (11.1) можно пользоваться для приближенных вычислений значений функции двух переменных в т.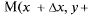

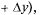близкой к т. М(х, у), если известны значения функции и ее частных производных в самой т. М.

Пример: Скорость истечения газа, находящегося под высоким давлением 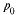в сосуде, через отверстие в стенке вычисляют по формуле

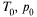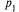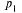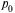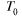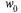где k, R — величины, зависящие от химического состава газа, — температура и давление в сосуде, — давление в окружающей среде. Пусть значения к = 1,5, R = 294, = 0,1, = 100, =617 =500.

Найти скорость истечения газа при изменениях 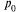до 108, 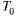до 600, R до 300.

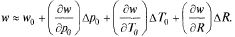
Находим производные. Они равны соответственно:

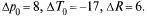Тогда 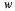=500 + 0,0817 · 8 + 0,397 · (-17) + + 0,0833 · 6 = 498,89. Непосредственное вычисление дает 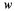= 494