Функция f:N® X, областью определения которой является множество натуральных чисел, называется последовательностью.

Если f:N® R, то последовательность называется числовой. Иначе, числовая последовательность – это функция натурального аргумента: x_n = f(n). Обозначают числовую последовательность {x_n}. Примеры числовых последовательностей:

Пример 16. 1) 1,2,..., n,...;
2) 1,-1,1,-1,...,(-1)ⁿ,...;
3) 1,1/2,1/3,...,1/n,....

Последовательность называется ограниченной сверху (снизу), если $ M (m), такое, что для любого nÎ N x_n£ M (x_n³ m).

Последовательность называется ограниченной, если она ограничена и сверху и снизу, то есть $ c > 0 такое, что |x_n| £ c для любого nÎ N. Заметим, что в данном определении c=max{|m|,|M|}.

Пример 17.

1,2,...,n,... — ограничена снизу, но неограничена сверху;

{1/n} – ограничена, так как 0< x_n£ 1 ;

{(-1)ⁿ} – ограничена

Последовательность x_n называется неограниченной, если

" c>0 $ N: |x_N| > c

Неограниченная последовательность может быть односторонне ограниченной, то есть ограниченной или сверху, или снизу. Пример неограниченной сверху последовательности: x_n = n.

Понятие предела числовой последовательности хорошо иллюстрируется на следующем примере. Пусть задана последовательность x_n = 1/n. Изобразим ее члены точками на числовой оси (рис. 12).

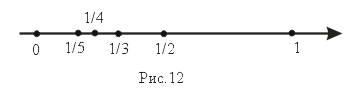
Можно заметить, что члены последовательности с ростом номера n как угодно близко приближаются к 0. При этом величина x_n становится все меньше и меньше. Очевидно, что пределом данной последовательности будет 0.

Дадим строгое определение предела числовой последовательности.

определение предела последовательности. Число A называется пределом последовательности x_n, если

" U(A) $ N: " n > N x_n Î U(A).

Приведем другое определение предела, которое является эквивалентным первому.

 определение предела последовательности. Число A называется пределом x_n, если

" e > 0 $ N: " n > N |x_n-A |< e

Заметим, что здесь использованы логические символы: квантор всеобщности " (вместо слова "для любого") и квантор существования $ (вместо слова "найдется").

Предел числовой последовательности обозначается lim_n®¥ x_n = A или x_n® A при n® ¥. Последовательность, имеющая предел, называется сходящейся, в противном случае расходящейся.

Пример 18. Пусть x_n = 1/n, покажем, что

lim_{n® ¥}1/n = 0.

Для этого запишем определение:

" e>0 $ N: " n>N |x_n|<e.

То есть 1/n<e при n>N=[1/e].

Пример 19.

x_n = .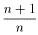

Доказать, что

lim_{n ® ¥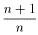} = 1

" e >0 $ N: " n > N | 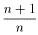-1| < e.
1/n < e Þ n > 1/e N = [1/e]
Если e = 1/10 , то N=10 и при n > 10 следует выполнение нужного неравенства.

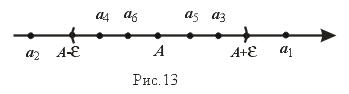
Выясним геометрический смысл понятия предела последовательности. Расположим члены последовательности x₁,x₂,..., x_n,... на числовой прямой. Неравенство |x_n-A|<e равносильно следующему A- e < x_n < A + e, которое говорит о том, что члены последовательности x_n попадают в e - окрестность точки A (рис.13). Вне этой e -окрестности может быть лишь конечное число членов данной последовательности.