Определение. Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.
Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора.
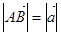
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых. Нулевой вектор коллинеарен любому вектору.
Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
Определение. Линейными операциями над векторами называется сложение и умножение на число.
Суммой векторов является вектор -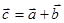 
Произведение -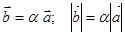 
, при этом 
коллинеарен 
.
Вектор сонаправлен с вектором ( ), если a > 0.
Вектор противоположно направлен с вектором ( ¯ ), если a < 0.
Скалярное произведение векторов. Угол между двумя векторами.
Определение. Скалярным произведением векторов и называется число, равное произведению длин этих сторон на косинус угла между ними.
× = ï ïï ïcosj
Свойства скалярного произведения:
1) × = ï ï2;
2) × = 0, если ^ или = 0 или = 0.
3) × = × ;
4) ×( + 
) = × + × ;
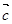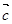5) (m )× = ×(m ) = m( × ); m=const
Если рассматривать векторы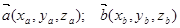 
в декартовой прямоугольной системе координат, то
× = xa xb + ya yb + za zb;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:
;
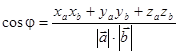Пример. Найти (5 + 3 )(2 - ), если 
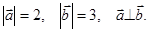
10 × - 5 × + 6 × - 3 × = 10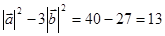 
,
т.к.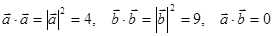 
.
Пример. Найти угол между векторами и , если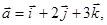 
.
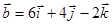Т.е. = (1, 2, 3), = (6, 4, -2)
× = 6 + 8 – 6 = 8:
.
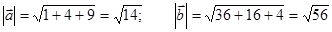cosj =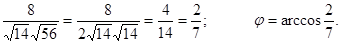 
Пример. Найти скалярное произведение (3 - 2 )×(5 - 6 ), если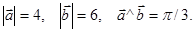 
15 × - 18 × - 10 × + 12 × = 15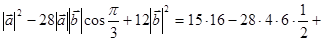 
+ 12×36 = 240 – 336 + 432 = 672 – 336 = 336.
Пример. Найти угол между векторами и , если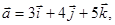 
.
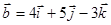Т.е. = (3, 4, 5), = (4, 5, -3)
× = 12 + 20 - 15 =17 :
.
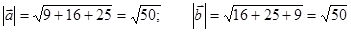cosj =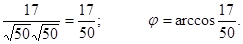 
Пример. При каком m векторы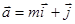 
и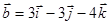 
перпендикулярны.
= (m, 1, 0); = (3, -3, -4)
.
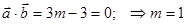Пример. Найти скалярное произведение векторов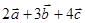 
и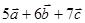 
, если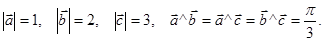 
( )( ) = 
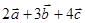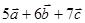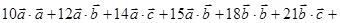
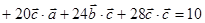
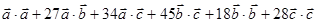= 10 +
+ 27 + 51 + 135 + 72 + 252 = 547.
Координаты вектора. Действия над векторами, заданными своими координатами.
Определение.
1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
3)Базисом на прямой называется любой ненулевой вектор.
Определение. Если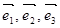 
- базис в пространстве и 
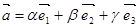, то числа a, b и g - называются компонентами или координатами вектора 
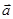в этом базисе.
В связи с этим можно записать следующие свойства:
- равные векторы имеют одинаковые координаты,
- при умножении вектора на число его компоненты тоже умножаются на это число,
= 
.
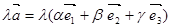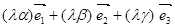- при сложении векторов складываются их соответствующие компоненты.
; 
;
+ 
= 
.
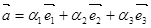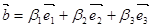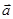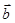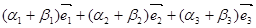Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат.
1-я ось – ось абсцисс
2-я ось – ось ординат
3-я ось – ось апликат
Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала.
Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то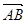 
= (x2 – x1, y2 – y1, z2 – z1).
Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.
Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х1, y1, z1), B(x2, y2, z2), то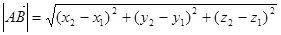 
.
Если точка М(х, у, z) делит отрезок АВ в соотношении l / m, считая от А, то координаты этой точки определяются как:
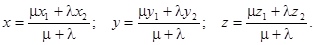
В частном случае координаты середины отрезка находятся как:
x = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2.
Линейные операции над векторами в координатах.
Пусть заданы векторы в прямоугольной системе координат
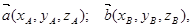тогда линейные операции над ними в координатах имеют вид:
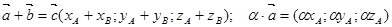
Дата: 2019-12-22, просмотров: 258.
