Рассмотрим некоторые типы интегралов, содержащих иррациональные функции.

Интегралы типа 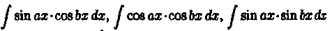называют неопределенными интегралами от квадратичных иррациональностей. Их можно найти следующим обpaзoм:

под радикалом выделить полный квадрат

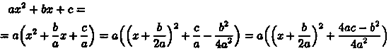
и сделать подстановку х +b/2a=t. При этом первые два интеграла приводятся к табличным, а третий - к сумме двух табличных интегралов.

Пример Найти интегралы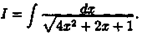

Решение: Так как,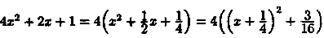

то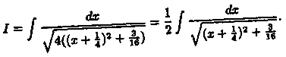

Cдeлаем подстановку x+1/4=t, x=t-1/4,dx=dt. Тогда

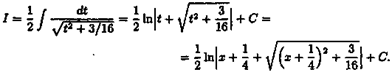
Интегралы типа , где Р_n(х) - многочлен степени n, можно вычислять, пользуясь формулой

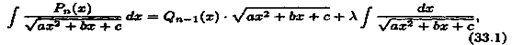                                                         1.                                                                                                                                                                 

где Q_n-1(x) - многочлен степени n-1 с неопpедeлeнными коэффициентами, l - также неопределенный коэффициент.

Все неопределенные коэффициенты находятся из тождества, получаемого дифференцированием обеих частей равенства (1):

после чего необходимо приравнять коэффициенты при одинаковых степенях неизвестной х.

Пример Найти интеграл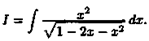

Решение: По формуле (1) имеем:

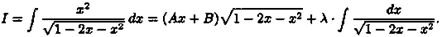
Дифференцируя это равенство, получаем:

Сравниваем коэффициенты при одинаковых степенях х:

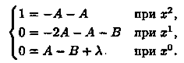
Отсюда А=-1/2,B=3/2,l=2. Следовательно,

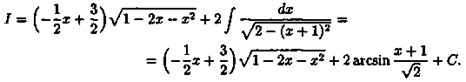
Дробно-линейная подстановка

Интегралы типа 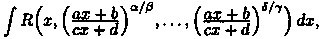где а, b, с, d - действительные числа, a,b,...,d,g - натуральные числа, сводятся к интегралам от рациональной функции путем подстановки где К - наименьшее общee кратное знаменателей дробей

Действительно, из подстановки следует, что 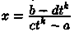и

т. е. х и dx выражаются через рациональные функции от t. При этом и каждая степень дроби выражается через рациональную функцию от t.

Пример Найти интеграл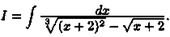

Решение: Наименьшее общee кратное знаменателей дробей 2/3 и 1/2 есть 6.

Поэтому полагаем х+2=t⁶, х=t⁶-2, dx=6t⁵ dt, 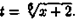Следовательно,

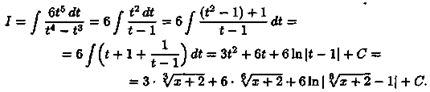
Пример Указать подстановку для нахождения интегралов:

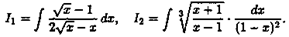
Решение: Для I₁ подстановка х=t², для I₂ подстановка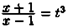

Тригонометрическая подстановка

Интегралы типа приводятся к интегралам от функций, рационально зависящих от тригонометрических функций, с помощью следующих тригонометрических подстановок: х=а•sint для первого интеграла; х=а•tgt для второго интеграла; 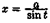для третьего интеграла.

Интегралы типа

Здесь подынтегральная функция есть рациональная функция относительно х и 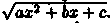Выделив под радикалом полный квадрат и сделав подстановку 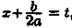, интегралы указанного типа приводятся к интегралам уже pасcмoтpeннoгo типа, т. е. к интегралам типа 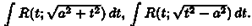Эти интегралы можно вычислить с помощью соответствующих тригонометрических подстановок.

Пример Найти интеграл

Решение: Так как х²+2х-4=(х+1)²-5, то х+1=t, x=t-1, dx=dt. Поэтому 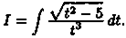Положим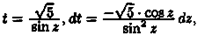

Тогда

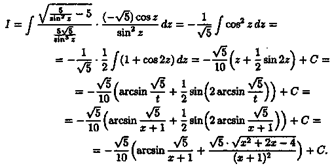
Замечание: Интеграл типа 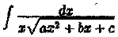целессooбразно находить с помощью подстановки х=1/t.