через две точки.

           Если на прямой в пространстве отметить две произвольные точки M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:

.

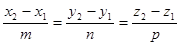           Кроме того, для точки М₁ можно записать:

.

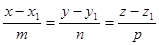           Решая совместно эти уравнения, получим:

.

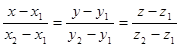Это уравнение прямой, проходящей через две точки в пространстве.

Общие уравнения прямой в пространстве.

           Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.

           Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:

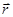× + D = 0, где

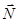- нормаль плоскости; 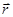- радиус- вектор произвольной точки плоскости.

           Пусть в пространстве заданы две плоскости: 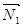× 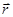+ D₁ = 0 и 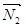× 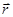+ D₂ = 0, векторы нормали имеют координаты: 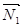(A₁, B₁, C₁), 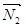(A₂, B₂, C₂); 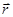(x, y, z).

           Тогда общие уравнения прямой в векторной форме:

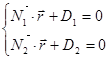
           Общие уравнения прямой в координатной форме:

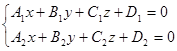
           Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.

           Для этого надо найти произвольную точку прямой и числа m, n, p.

           При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.

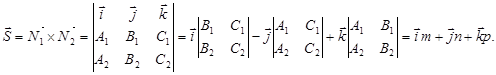
           Пример. Найти каноническое уравнение, если прямая задана в виде:

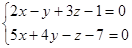
           Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.

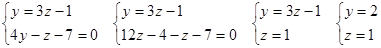, т.е. А(0, 2, 1).

           Находим компоненты направляющего вектора прямой.

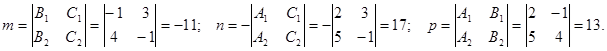
           Тогда канонические уравнения прямой:

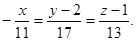
Пример. Привести к каноническому виду уравнение прямой, заданное в виде:

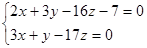
           Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда:

;

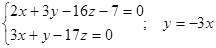2x – 9x – 7 = 0;

x = -1; y = 3;

           Получаем: A(-1; 3; 0).

Направляющий вектор прямой: .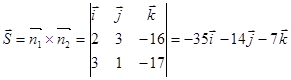

Итого: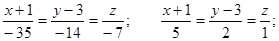

18. Понятие функции. Способы задания функции.

Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости (связи) между элементами двух множеств.

Пусть даны два непустых множества X и Y. Соответствие ƒ, которое каждому элементу хÎ X сопоставляет один и только один элемент уÎ Y, называется функцией и записывается у=ƒ(х), хÎ X или ƒ: X→Y. Говорят еще, что функция ƒ отображает множество X на множество Y.

Числовые функции. График функции. Способы задания функций

Пусть задана функция ƒ : X→Y.

Если элементами множеств X и Y являются действительные числа (т. е. XÌ R и YÌ R), то функцию ƒ называют числовой функцией. В дальнейшем будем изучать (как правило) числовые функции, для краткости будем именовать их просто функциями и записывать у=ƒ(х).

Переменная х называется при этом аргументом или независимой переменной, а у — функцией или зависимой переменной (от х). Относительно самих величин х и у говорят, что они находятся в функциональной зависимости. Иногда функциональную зависимость у от х пишут в виде у=у(х), не вводя новой буквы (ƒ) для обозначения зависимости.

Частное значение функции ƒ(х) при х=a записывают так: ƒ(a). Например, если ƒ(х)=2х²-3, то ƒ(0)=-3, ƒ(2)=5.

Графиком функции у=(х) называется множество всех точек плоскости Оху, для каждой на которых х является значением аргумента, а у — соответствующим значением функции.

Чтобы задать функцию у=ƒ(х), необходимо указать правило, позволяющее, зная х, находить соответствующее значение у.

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

Аналитический способ : функция задается в виде одной или нескольких формул или уравнений.

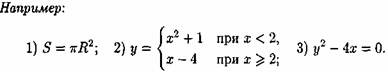
Если область определения функции у = ƒ(х) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл.Так, областью определения функции у= √(1-х2) является отрезок [-1; 1].

Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию у=ƒ(х).