Определение. Функция f(x), определенная в окрестности некоторой точки х₀, называется непрерывной в точке х₀, если предел функции и ее значение в этой точке равны, т.е.

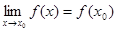
Тот же факт можно записать иначе: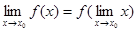

Определение. Если функция f(x) определена в некоторой окрестности точки х₀, но не является непрерывной в самой точке х₀, то она называется разрывной функцией, а точка х₀ – точкой разрыва.

Определение. Функция f(x) называется непрерывной в точке х₀, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию

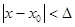
верно неравенство                          .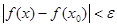

           Определение. Функция f(x) называется непрерывной в точке х = х₀, если приращение функции в точке х₀ является бесконечно малой величиной.

f(x) = f(x₀) + a(x)

где a(х) – бесконечно малая при х®х₀.

Свойства непрерывных функций.

1) Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.

2) Частное двух непрерывных функций 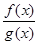– есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

           3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х₀, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.

           Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.

Точки разрыва и их классификация.

           Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х₀, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х₀ является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.

Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.

           Если односторонний предел 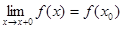, то функция называется непрерывной справа.

Если односторонний предел 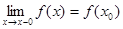, то функция называется непрерывной слева.

Определение. Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

Определение. Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

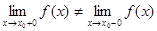
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х₀, достаточно того, что она определена слева и справа от нее.

Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.

Определение. Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

Пример. Функция f(x) = 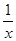 имеет в точке х₀ = 0 точку разрыва 2 – го рода, т.к.

.

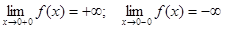           Пример. f(x) =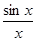

Функция не определена в точке х = 0, но имеет в ней конечный предел 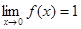, т.е. в точке х = 0 функция имеет точку разрыва 1 – го рода. Это – устранимая точка разрыва, т.к. если доопределить функцию:

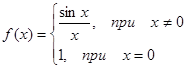
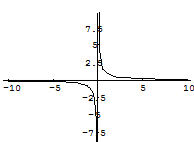
График этой функции:

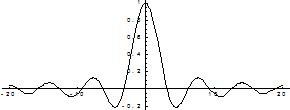
Таким образом, для того, чтобы точка разрыва 1 – го рода была устранимой, необходимо, чтобы односторонние пределы справа и слева были конечны и равны, а функция была бы в этой точке не определена.