Определение. Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенство
ïf(x)ï>M
выполняется при всех х, удовлетворяющих условию
0 < ïx - aï < D
Записывается 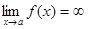 .
.
Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:
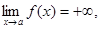
а если заменить на f(x)<M, то:
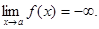
Определение. Функция называется бесконечно большой при х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если 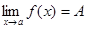 , где А – число или одна из величин ¥, +¥ или -¥.
, где А – число или одна из величин ¥, +¥ или -¥.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f ( x ) ® 0 при х ® а (если х ® ¥ ) и не обращается в ноль, то
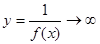
Сравнение бесконечно малых функций.
Пусть a(х), b(х) и g(х) – бесконечно малые функции при х ® а. Будем обозначать эти функции a, b и g соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Например, функция f(x) = x10 стремится к нулю быстрее, чем функция f(x) = x.
Определение. Если 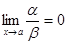 , то функция a называется бесконечно малой более высокого порядка, чем функция b.
, то функция a называется бесконечно малой более высокого порядка, чем функция b.
Определение. Если 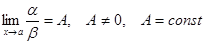 , то a и b называются бесконечно малыми одного порядка.
, то a и b называются бесконечно малыми одного порядка.
Определение. Если 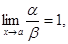 то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
то функции a и b называются эквивалентными бесконечно малыми. Записывают a ~ b.
Пример. Сравним бесконечно малые при х®0 функции f(x) = x10 и f(x) = x.
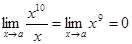
т.е. функция f(x) = x10 – бесконечно малая более высокого порядка, чем f(x) = x.
Определение. Бесконечно малая функция a называется бесконечно малой порядка k относительно бесконечно малой функции b, если предел 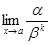 конечен и отличен от нуля.
конечен и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 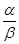 не имеет предела, то функции несравнимы.
не имеет предела, то функции несравнимы.
Пример. Если 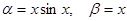 , то при х®0
, то при х®0 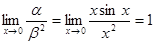 , т.е. функция a - бесконечно малая порядка 2 относительно функции b.
, т.е. функция a - бесконечно малая порядка 2 относительно функции b.
Пример. Если 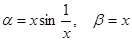 , то при х®0
, то при х®0 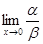 не существует, т.е. функция a и b несравнимы.
не существует, т.е. функция a и b несравнимы.
Первый и второй замечательные пределы.
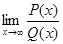 , где P(x) = a0xn + a1xn-1 +…+an,
, где P(x) = a0xn + a1xn-1 +…+an,
Q(x) = b0xm + b1xm-1 +…+bm - многочлены.
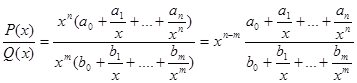
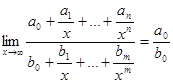
Итого: 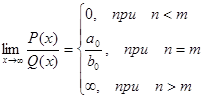
Первый замечательный предел. 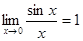
Второй замечательный предел. 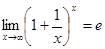
Часто если непосредственное нахождение предела какой – либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:
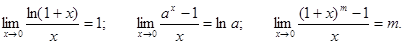
Пример . Найти предел.
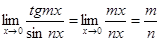
Пример . Найти предел.
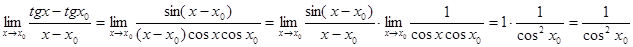
Дата: 2019-12-22, просмотров: 376.