Выборочный метод ‑ статистический прием, который базируется на некоторых положениях закона больших чисел. Он широко используется в формировании массива маркетинговой информации, поскольку дает возможность экономить значительные средства, позволяет ускорить получение нужных сведений, обеспечивает сбор сведений, которые иным способом получить невозможно.
Выборка или выборочная совокупность ‑ часть генеральной совокупности элементов, которая охватывается маркетинговым исследованием. Выборка – это часть потребителей, которые будут представлять интересы и вкусы всех потребителей генеральной совокупности.
Применение выборки требует строгого соблюдения нескольких требований:
‑ отбор не должен быть преднамеренным, т. е. все единицы совокупности должны иметь равную возможность попасть в выборочную совокупность;
‑ размер совокупности, из которой ведется отбор, должна быть достаточно большой, чтобы действовал закон больших чисел;
‑ необходимо обеспечить качественную однородность отобранной совокупности.
Этапы построения выборки следующие:
Этап 1. Определение исследуемой совокупности ‑ первая стадия построения выборки. Исследуемая совокупность ‑ множество элементов или объектов, которые обладают интересующей исследователя информацией и о которых требуется сделать выводы. Определить исследуемую совокупность означает принять решение о том, какие элементы или объекты должны иметь шанс быть включенными в выборку, а какие ‑ нет. Например, дети и подростки в возрасте от 8 до 17 лет, посещающие школу в европейской части России.
Этап 2. Основа для построения выборки. Представляет собой списки элементов исследуемой совокупности или правила нахождения этих элементов (например, телефонная или адресная книги, список предприятий отрасли, географическая карта). Примером правил нахождения элементов исследуемой совокупности может послужить список семизначных телефонных номеров, перемешанных случайным образом.
Этап 3. Способы построения выборки. Существуют две группы методов построения выборки в той или иной степени реализующих репрезентацию мнений и позиций генеральной совокупности: вероятностные и детерминированные.
‑ Вероятностные методы основаны на использовании теории вероятности и базируются на том, что репрезентация будет достигнута в случае, если каждой единице генеральной совокупности будет обеспечено равновероятное попадание в выборку. Например, если генеральной совокупностью является все взрослое (16‑85 лет) население города ‑ 200 тыс. чел., то каждому жителю должна быть обеспечена равная вероятность стать участником исследования, попасть в выборку, равная 1/200000. В противном случае выборка будет не случайной, а смещенной, т. е. менее репрезентативной.
Виды вероятностных методов формирования выборки:
простая случайная выборка ‑ каждый элемент отбирается независимо и имеет равную вероятность попасть в выборку;
систематическая выборка: первый элемент выбирается произвольно, затем выбирают каждый i-й элемент;
стратифицированная выборка: генеральная совокупность делится на подгруппы (страты). Элементы выбираются случайным образом из каждой страты;
кластерная выборка: совокупность делится на непересекающиеся кластеры. Случайным образом отбираются несколько кластеров. Затем производится сплошное или выборочное обследование отобранных кластеров.
Детерминированные методы построения выборки ‑ отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям ‑ доступности, типичности, равного представительства и т. д.
Этап 4. Определение необходимого размера выборки. На практике используется несколько подходов к определению объема выборки.
1). Произвольный подход, основанный на применении «правила большого пальца». Например, бездоказательно принимается, что для получения точных результатов выборка должна составлять 5 % от совокупности. Данный подход простой и доступный в исполнении, не позволяет получать точные результаты. Его достоинством является относительная дешевизна затрат.
2). Подход на основе заранее оговоренных условий. Заказчик маркетингового исследования, например, знает, что при изучении общественного мнения выборка обычно составляет 1000–1200 чел., поэтому он рекомендует исследователю придерживаться данной цифры.
Необходимый размер выборки можно приблизительно оценить, зная, в каких он обычно пределах находится в аналогичных исследованиях (табл. 11).
Таблица 11
Минимальный и типичный размеры выборки при разных исследованиях
| Задачи исследования | Минимальный размер выборки | Типичный размер выборки |
| Выявление проблем (например, оценка потенциала выборки) | 500 | 1000‑2500 |
| Решение проблем (например, относительно цены товара) | 200 | 300‑500 |
| Тестирование товара | 200 | 300‑500 |
| Тестирование рекламы (в расчете на 1 рекламный продукт) | 150 | 200‑300 |
3). Определение объема выборки исходя из стоимости проведения опроса. Хотя при этом ценность и достоверность получаемой информации не принимается в расчет.
4). Определение объема выборки на основе статистического анализа. Данный подход предполагает определение минимального объема выборки с учетом требований к надежности и достоверности получаемых результатов.
5). Определение объема выборки на основе расчета доверительного интервала.
Под «достоверностью», уровнем достоверности понимают показатель вероятности того, что истинное значение изучаемого параметра генеральной совокупности попадет в доверительный интервал. Чем выше задаваемый уровень достоверности, тем больше должна быть выборка.
Под доверительным интервалом понимают диапазон, в который попадет истинное значение изучаемого параметра генеральной совокупности при данном уровне достоверности. Чем он меньше, тем больше должна быть выборка.
Доверительный интервал – это диапазон, крайние точки которого характеризуют процент определенных ответов на какой-то вопрос.
Данное понятие тесто связано с понятием «среднее квадратичное отклонение получаемого признака в генеральной совокупности». Чем оно больше, тем шире должен быть доверительный интервал, чтобы включить в свой состав, например 95 % ответов.
Из свойств нормальной кривой распределения вытекает, что конечные точки доверительного интервала, равного, к примеру, 95 % определяются как произведение: 1,96 (нормированное отклонение) и среднего квадратичного отклонения. Числа 1,96 и 2,58 (для 99 % доверительного интервала) обозначаются как z.
В табл. 12 представлены величины z для различных доверительных интервалов. Доверительный интервал равный 95 % или 99 % является стандартным при проведении маркетинговых исследований.
Таблица 12
Значение нормированного отклонения оценки z от среднего значения в зависимости от доверительной вероятности (а) полученного результата
| а, % | 60 | 70 | 80 | 90 | 90 | 95 | 97 | 99,0 | 99,7 |
| z | 0,84 | 1,03 | 1,29 | 1,44 | 1,65 | 1,96 | 2,18 | 2,58 | 3,0 |
Именно доверительный интервал именуют «допустимой погрешностью» выборки. Ее исследователи задают (назначают) сами или рассчитывают по специальным формулам в зависимости от заданного объема выборки.
Индикатором степени отличия оценки, истинной для совокупности в целом, которая ожидается для типичной выборки, является среднеквадратическая ошибка. К примеру, исследуется мнение потребителей о новом товаре и заказчик данного исследования указал, что его устроит точность полученных результатов, равная плюс минус 5 %.Предположим, что 30 % членов выборки высказались за новый продукт. Это означает, что диапазон возможных оценок для всей совокупности составляет 25–35 %. Причем, чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.
Если генеральная совокупность очень велика (более 10 тыс., более 100 тыс.), существует несколько видов формул для расчета объема выборки в зависимости от исходных условий.
1). Формула для расчета необходимого объема выборки при известном среднем отклонении (дисперсии) и заданных уровнях достоверности и точности.
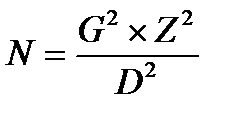 (1)
(1)
где
N ‑ искомый объем выборки;
G ‑ дисперсия признака, ожидаемое среднее отклонение получаемых результатов от ожидаемого среднего значения;
Z ‑ коэффициент уровня достоверности (2 ‑ для 0,95; 3 ‑ для 0,99);
D ‑ желаемый уровень точности, доверительный интервал, допустимая погрешность.
2). Формула расчета объема выборки в зависимости от ожидаемых ответов «да»
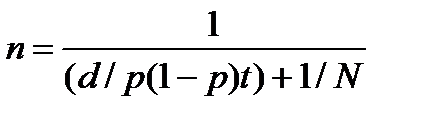 (2)
(2)
где n ‑ искомый объем генеральной выборки;
d ‑ квадрат ошибки выборки, допустимая погрешность (задается по желанию исследователя);
p ‑ ожидаемая доля ответов «да»;
t ‑ квадрат значения статистики Стьюдента, коэффициент уровня достоверности;
N ‑ размер генеральной совокупности.
3). Формула для расчета выборки для опроса с простыми альтернативными вопросами по принципу «Да/Нет». Когда на заданный вопрос существует только два варианта ответов, выраженных в процентах (используется процентная мера), объем выборки определяется по следующей формуле:
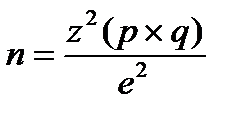 (3)
(3)
где n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности;
р – найденная вариация для выборки;
q = (100 – p);
е – допустимая ошибка.
Если генеральная совокупность все же больше 400, но менее 10000, то объем выборки можно взять из табл. 13.
Если респондентов (людей, домохозяйств, организаций, муниципальных образований и т. д.) совсем мало (менее 400), то выборку построить не удастся. Надо проводить сплошное обследование («цензус»). В лучшем случае в нем примут участие до половины членов генеральной совокупности.
Таблица 13
Рекомендуемый объем выборки при «малой» генеральной совокупности
| Объем генеральной совокупности | Рекомендуемый объем выборки |
| 500 | 220 |
| 1000 | 280 |
| 2000 | 330 |
| 3000 | 350 |
| 5000 | 370 |
| 7000 | 385 |
| 10000 | 400 |
Обычно, если выборка составляет менее 5 % совокупности, то совокупность считается большой, и расчеты проводятся по вышеприведенным правилам.
Если же объем выборки превышает 5 % совокупности, то последняя считается малой, и в вышеприведенные формулы вводится поправочный коэффициент. Объем выборки в данном случае определяется следующим образом:
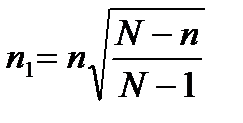 (4)
(4)
где n1 – объем выборки для малой совокупности,
n – объем выборки (или для процентных мер или для средних), рассчитанный по приведенным выше формулам,
N – объем генеральной совокупности.
Этап 5. Реализация процесса построения выборки. Для построения выборки нужно детально определить, как конкретно будут воплощаться в жизнь все решения, о которых говорилось выше ‑ об исследуемой совокупности, об основе выборки, о единицах отбора, о способе построения выборки и о ее размере. Так, если единицами отбора являются домохозяйства, необходимо четко определить, какие именно домохозяйства имеются в виду. Необходимо решить, что делать, если в нужной квартире никого нет дома, например, предусмотреть повторные визиты или звонки.
В частности, очень важно решить, как будут отбираться респонденты в семьях, т. е. в случае, если единицами отбора являются семьи, а элементами выборки ‑ один член семьи. Кого нужно опрашивать? Того, кто открыл дверь или ответил на звонок? А если нет, то в инструкциях нужно предусмотреть все ситуации, которые могут возникнуть. Нередко условиям отбора респондента удовлетворяют два или более члена семьи. Например, если в исследовании о способах проведения досуга интервьюер изъявит желание побеседовать с главой семьи, то может оказаться, что эти функции исполняют и муж, и жена одновременно. В таких ситуациях в качестве одного из вероятностных способов построения выборки применим метод ближайшего дня рождения: опрашивается подходящий по параметрам член семьи, у которого раньше наступит день рождения.
Дата: 2019-12-09, просмотров: 452.