Решение матричных игр в смешанных стратегиях может быть найдено либо графически, либо методами линейного программирования. Графический метод применим для решения игр, в которых хоть один игрок имеет две чистые стратегии. Этот метод интересен в том плане, что графически объясняет понятие седловой точки. Методами линейного программирования может быть решена любая игра двух лиц с нулевой суммой.
ГРАФИЧЕСКОЕ РЕШЕНИЕ ИГР. Рассмотрим игру 2 x n, в которой игрок А имеет две стратегии.
Игра предполагает, что игрок А смешивает стратегии А1и А2с соответствующими вероятностями x1и 1 –х1, 0 ≤ x1 ≤ 1. Игрок В смешивает стратегии В1, В2,..., Вn с вероятностями у1, у2, ...,уп, где yj ≥ 0,j = 1, 2,..., и, y1 + у2 + …+ уn = 1. В этом случае ожидаемый выигрыш игрока А, соответствующий j-й чистой стратегии игрока В, вычисляется в виде
Следовательно, игрок А ищет величину х1, которая максимизирует минимум ожидаемых выигрышей
 .
.
Пример 3.6-3
Рассмотрим следующую игру 2x4, в которой платежи выплачиваются игроку А.
| B1 | B2 | B3 | B4 | |
| A1 | –1 | |||
| A2 |
Игра не .имеет решения в чистых стратегиях, и, следовательно, стратегии должны быть смешанными. Ожидаемые выигрыши игрока А, соответствующие чистым стратегиям игрока В, приведены в следующей таблице.
| Чистые стратегии игрока В | Ожидаемые выигрыши игрока А |
| –2x1 + 4 | |
| –x1 + 3 | |
| x1 + 2 | |
| –7x1 + 6 |
На рис. 14.6 изображены четыре прямые линии, соответствующие чистым стратегиям игрока В. Чтобы определить наилучший результат из наихудших, построения нижняя огибающая четырех указанных прямых (изображенная на рисунке толстыми линейными сегментами), которая представляет минимальный (наихудший) выигрыш для игрока А независимо от того, что делает игрок В. Максимум (наилучшее) нижней огибающей соответствует максиминному решению в точке х1* = 0.5. Эта точка определяется пересечением прямых 3 и 4. Следовательно, оптимальным решением для игрока А является смешивание стратегий A1 и A2вероятностями 0.5 и 0.5 соответственно. Соответствующая цена игры v определяется подстановкой х1= 0.5 уравнение либо прямой 3, либо 4, что приводит к следующему.
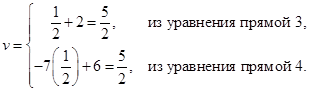

рис. 14.6
Оптимальная смешанная стратегия игрока В определяется двумя стратегиями, которые определяют нижнюю огибающую графика. Это значит, что игрок В может смешивать стратегии B3 и В4, в этом случае у1 = y2 = 0 и у4 = 1 – у3. Следовательно, ожидаемые платежи игрока В, соответствующие чистым стратегиям игрока А, имеют следующий вид.
| Чистые стратегии игрока В | Ожидаемые выигрыши игрока А |
| 4ό3 – 1 | |
| –4ò3 + 6 |
Наилучшее решение из наихудших для игрока В представляет собой точку минимума верхней огибающей заданных двух прямых (построение прямых и определение верхней огибающей будет для Вас поучительным). Эта процедура эквивалентна решению уравнения
 .
.
Его решением будет у3 = 7/8, что определяет цену игры v = 4 х (7/8) – 1 = 5/2.
Таким образом, решением игры для игрока А является смешивание стратегий А1 и А2равными вероятностями 0.5 и 0.5, а для игрока В – смешивание стратегий В3 и В4 с вероятностями 7/8 и 1/8. (В действительности игра имеет альтернативное решение для игрока В, так как максиминная точка на рис. 14.6 определяется более чем двумя прямыми. Любая выпуклая линейная комбинация этих альтернативных решений также является решением задачи.)
Для игры, в которой игрок А имеет m стратегий, а игрок В – только две, решение находится аналогично. Главное отличие состоит в том, что здесь строятся графики функций, представляющих ожидаемые платежи второго игрока, соответствующие чистым стратегиям игрока А. В результате ведется поиск минимаксной точки верхней огибающей построенных прямых.
Упражнения 3.6,b
1. Решите графически игру с подбрасыванием монет из примера 3.6-2.
2. Робин часто путешествует между двумя городами. При этом есть возможность выбирать один из двух маршрутов: маршрут А представляет собой скоростное шоссе в четыре полосы, маршрут В –длинную обдуваемую ветром дорогу. Патрулирование дорог осуществляется ограниченным числом полицейских. Если все полицейские расположены на одном маршруте, Робин с ее страстным желанием ездить очень быстро, несомненно, получит штраф в 100 долларов за превышение скорости. Если полицейские патрулируют на двух маршрутах в соотношении 50 на 50, то имеется 50%-ная вероятность, что Робин получит штраф в 100 долларов на маршруте А и 30%-ная вероятность, что она получит такой же штраф на маршруте В. Кроме того, маршрут В длиннее, поэтому бензина расходуется на 15 долларов больше, чем на маршруте А. Определите стратегию как для Робин, так и для полиции.
3. Решите графически следующие игры, в которых платежи выплачиваются игроку А.
а)
| B1 | B2 | B3 | |
| A1 | –3 | ||
| A2 | –6 |
b)
| B1 | B2 | |
| A1 | ||
| A2 | ||
| A3 |
4. Дана следующая игра двух лиц с нулевой суммой.
| B1 | B2 | B3 | |
| A1 | 5.0 | 50.0 | 50.0 |
| A2 | 1.0 | 1.0 | 0.1 |
| A3 | 10.0 | 1.0 | 10.0 |
a) Проверьте, что смешанные стратегии с вероятностями (1/6, 0, 5/6) для игрока А и с вероятностями (49/54, 5/54, 0) для игрока В являются оптимальными, и определите цену игры.
b) Покажите, что цена игры равна
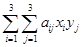 .
.
решение матричных игр методами линейного программирования. Теория игр находится в тесной связи с линейным программированием, так как любую конечную игру двух лиц с нулевой суммой можно представить в виде задачи линейного программирования и наоборот. Дж. Данциг [2] отмечает, что когда в 1947 году создатель теории игр Дж. фон Нейман впервые ознакомился с симплекс-методом, он сразу установил эта взаимосвязь и обратил особое внимание на концепцию двойственности в линейном программировании. Этот раздел иллюстрирует решение матричных игр методами линейного программирования.
Оптимальные значения вероятностей хi, i = 1, 2,..., m, игрока А могут быть определены путем решения следующей максиминной задачи.
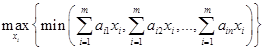 ,
,
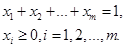
Чтобы сформулировать эту задачу в виде задачи линейного программирования, положим
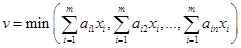 .
.
Отсюда вытекает, что
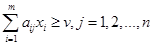 .
.
Следовательно, задача игрока А может быть записана в виде
Максимизировать z = v
при ограничениях
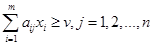 ,
,
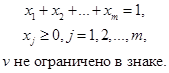
Отметим последнее условие, что цена игры v может быть как положительной, так и отрицательной.
Оптимальные стратегии у1, у2, ...,уn игрока В определяются путем решения задачи
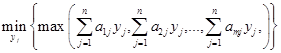
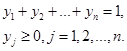
Используя процедуру, аналогичную приведенной выше для игрока А, приходим к выводу, что задача для игрока В сводится к следующему.
Минимизировать w = v
при ограничениях
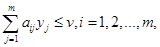
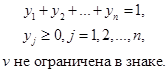
Две полученные задачи оптимизируют одну и ту же (не ограниченную в знаке) переменную v, которая является ценой игры. Причиной этого является то, что задача игрока В является двойственной к задаче игрока А (вам предлагается доказать это утверждение в упр. 3.5,с(6), используя определение двойственности). Это означает, что оптимальное решение одной из задач автоматически определяет оптимальное решение другой.
Пример 3.6-4
Решим следующую матричную игру методами линейного программирования.
| B1 | B2 | B3 | Минимумы строк | |
| A1 | –1 | –3 | –3 | |
| A2 | –2 | –1 | –2 | |
| A3 | –5 | –6 | –6 | |
| Максимумы столбцов |
Значение цены игры v находится между –2 и 2.
Задача линейного программирования для игрока А
Максимизировать z = v
при ограничениях
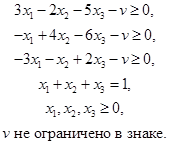
Оптимальным решением, полученным с помощью программы TORA, является
x1 = 0.3945, х2 = 0.3119, х3 = 0.2936 и v = – 0.9083.
Соответствующими двойственными переменными являются y1 = –0.3211, у2 = –0.0826, у3 = –0.5963. Причина того, что переменные у1, у2, у3 не являются положительными, как это должно быть, заключается в том, что задача линейного программирования для игрока А является задачей максимизации с ограничениями вида "≥". При этих условиях, как известно, соответствующе двойственные переменные должны быть отрицательными. Чтобы убедиться в том, что причина именно в этом, преобразуем все ограничения вид "≥" в задаче линейного программирования для игрока А в ограничения вида "≤" путем умножения каждого неравенства на –1. Соответствующие двойственные переменные будут неотрицательными, как и требуется (см. упр. 3.6,с(1)). Действительно, построение двойственной задачи непосредственно из задачи линейного программирования для игрока А показывает (см. упр. 3.6,с(6)), что в двойственной задаче, являющейся соответствующей задачей линейного программирования для игрока В, Должны быть уj ≤ 0, но в то же время требуется выполнение условия –y1 – у2 – ... – уn = 1, что равносильно требованиям уj ≥ 0 и y1 + у2 + ... + уn = 1. К счастью, проблем, связанных со знаками, можно избежать преобразуя ограничения–неравенства вида "≥" в задаче линейного программирования для игрока А в ограничения–неравенства вида "≤".
Задача линейного программирования для игрока В
Минимизировать z = v
при ограничениях
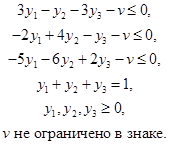
Оптимальным решением, полученным с помощью программы TORA, является
у1= 0.3211, у2 = 0.0826, уз = 0.5963 и v = –0.9083. Соответствующими двойственными переменными являются х1= –0.3945, х2= –0.3119, х3= –0.2936. Двойственные переменные отрицательны, ибо, подобно разобранной выше задаче для игрока А, в этом случае задача минимизации линейного программирования имеет ограничения–неравенства вида "≤". Приведение ограничений к виду "≥" исправит ситуацию со знаками.
Упражнений 3.6,с
1. Покажите в задаче из примера 3.6-4, что если ограничения–неравенства задачи линейного программирования для игрока А приведены к виду "≤", то аналогичные ограничения задачи для игрока В преобразуются в вид "≥" и двойственные переменные, полученные из одной или другой задачи, будут неотрицательными.
2. На загородном пикнике две команды, по два человека в каждой, играют в прятки. Есть четыре места, где можно спрятаться (А, Б, В и Г), и два члена прячущейся команды могут спрятаться каждый отдельно в любых двух из четырех мест. Затем другая команда имеет возможность проверить любые два места. Команда, которая ищет, получает премию, если будут обнаружены оба участника прячущейся команды, если же не обнаружен ни один участник, то она выплачивает премию. Иначе игра заканчивается вничью.
a) Сформулируйте задачу в виде игры двух лиц с нулевой суммой.
b) Определите оптимальные стратегии и цену игры.
c) Имеет ли задача альтернативные решения?
d) Является ли эта игра справедливой, т.е. имеет ли она цену, равную нулю?
3. Университетские команды UA и DU определяют свои стратегии игры в национальном чемпионате по баскетболу для колледжей. Оценивая возможности своих "запасных скамеек", каждый тренер разработал по четыре варианта замены игроков на протяжении игры. Способность каждой команды выполнять двух-, трех–очковые и штрафные броски является основным фактором, определяющим результат игры. Приведенная ниже таблица содержит очки чистого выигрыша команды UA на протяжении одного владения мячом в зависимости от стратегий, планируемых каждой командой.
| DU1 | DU2 | DU3 | DU4 | |
| UA1 | –2 | |||
| UA2 | –3 | |||
| UA3 | –1 | –2 | ||
| UA4 | –1 | –2 |
a) Решите игру методами линейного программирования и определите выигрышные стратегии.
b) Исходя из имеющейся информации, какая из двух команд может выиграть чемпионат?
c) Пусть за всю игру имеется 60 возможностей владения мячом (30 владений для каждой команды). Предскажите ожидаемое количество очков, с которым будет выиграна игра чемпионата.
4. Армия полковника Блотто сражается с вражеской армией за контроль над двумя стратегически важными позициями. Полковник имеет в своем распоряжении два полка, а его противник — три. Каждый из противников может посыпать на любую позицию только целое число полков или совсем не посылать. Позиция будет захвачена армией, которая атакует большим количеством полков. Иначе результат сражения является ничейным
a) Сформулируйте задачу в виде игры двух лиц с нулевой суммой и решите игр; методами линейного программирования.
b) Какая армия выиграет сражение?
5. В игре двух лиц, именуемой двухпальцевой игрой Морра, каждый игрок показывает один или два пальца и одновременно отгадывает число пальцев, которые покажет его противник. Игрок, который угадал, выигрывает сумму, равную суммарному числу показанных противниками пальцев. Иначе игра заканчивается вничью. Сформулируйте задачу в виде игры двух лиц с нулевой суммой и решите игру методами линейного программирования.
6. Покажите, что задача, двойственная к задаче линейного программирования для игрока А, является задачей линейного программирования для игрока В и что еле дующие два утверждения не противоречат друг другу.
a) Задача линейного программирования для игрока А записана в форме, приведенной в разделе 3.6.2.
b) Задача линейного программирования для игрока А записана в форме, упомянутой в п. а), в которой все ограничения вида "≥" приведены к виду "≤".
Заключение
В этой главе рассмотрены критерии выбора оптимальных решений как в ситуациях точными (детерминированными), так и неполными (вероятностными или неопределенными) данными. Дальнейшие приложения критериев выбора оптимальных решений в ситуациях с неполными данными будут рассмотрены в последующих главах. В частности, критерий ожидаемой величины используется в главах, посвященных управлению запасам) теории массового обслуживания, имитационному моделированию и марковским процесса принятия решений. Это вовсе не значит, что другие критерии неприменимы. Критерий ожидаемой величины используется скорее традиционно в силу своей простоты.
Литература
Chen S. and Hwang C. Fuzzy Multiple Decision Making, Springer – Verlag, Berlin, 1992.
Dantzing G. B. Linear Programming and Extension, Princeton University Press, Princeton, N. J., 1963.
Meyerson R. Game Theory: Analysis of Conflict, Harvard University Press, Cambridge, Mass., 1991.
Saaty T. L. Fundamentals of Decision Making, RWS Publications, Pittsburg, 1994.
Комплексные задачи
1. Руководитель цеха рассматривает три возможных решения относительно существующего фрезерного станка.
a) Модифицировать имеющийся станок, установив на нем автоматическую подачу (АП).
b) Купить новый станок с программным управлением (ПУ).
c) Заменить станок обрабатывающим центром (ОЦ).
Три альтернативы оцениваются на основе двух критериев: денежный и функциональный. Следующая таблица содержит необходимые данные.
| Критерий | Единицы | АП | ПУ | ОЦ |
| Денежный | ||||
| Начальная стоимость ($) | 12 000 | 25 000 | 120 000 | |
| Стоимость обслуживания ($) | 2 000 | 4 000 | 15 000 | |
| Стоимость обучения персонала ($) | 3 000 | 8 000 | 20 000 | |
| Функциональный | ||||
| Производительность | Изделий/день | |||
| Время наладки | Минут | |||
| Металлические отходы | Фунты/день |
Руководитель считает, что денежный критерий в полтора раза важнее функционального. Кроме того, производительность в два раза важнее времени наладки и в три раза важнее, чем количество получаемых металлических отходов. Показатель, связанный с временем наладки, считается в четыре раза важнее показателя, связанного с количеством металлических отходов. Что же касается денежного критерия, то руководитель считает, что стоимость обслуживания и стоимость обучения персонала одинаково важны, а начальная стоимость в два раза важнее каждого из этих двух показателей.
Проанализируйте описанную ситуацию и дайте соответствующие рекомендации.
2. Компания использует каталог товаров для продажи, включающий более 200 000 наименований, хранящихся на многих региональных складах. В прошлом компания считала важным иметь точный перечень запасов на каждом складе. Как следствие этого, каждый год проводился переучет — интенсивная и неприятная работа, которая неохотно выполнялась всеми складами. Компания для проверки качества складских операций в регионе сопровождала каждый переучет ревизией, которая охватывала около 100 наименований на каждом складе. Результаты проверки обнаружили, что в среднем лишь 64% наименований на каждом складе соответствовали действительной инвентарной описи, что является неприемлемым. Дабы исправить ситуацию, компания распорядилась чаще проводить переучет дорогих и быстро реализуемых товаров. Системному аналитику была поставлена задача разработать процедуры для реализации этих планов. Вместо того чтобы напрямую заняться выполнением задания компании, системный аналитик решил установить причину возникшей проблемы. Он перешел в своем исследовании от формулировки "Как мы можем увеличить частоту переучетов?" к "Как можно повысить точность переучетов?". Изучение проблемы под таким углом зрения свелось к следующему анализу. Предполагая, что доля точно сосчитанных наименований на складе равна р, аналитик затем предположил, что есть основания считать, что имеется 95%-ная вероятность того, что если изделие было правильно учтено в первый раз, то будет правильно переучтено и при последующем переучете. Для части 1 – р товаров, которая не была точно учтена в первом раунде проверки, доля правильного учета во втором раунде равна 80%. Используя эту информацию, аналитик с помощью дерева решений построил график безубыточности, который сравнил точность учета в первом и втором раундах проверки. Конечный результат сводился к тому, что склады, на которых уровень точности выше порога безубыточности, не требовали переучета. Удивительным результатом предложенного решения было рьяное усилие со стороны каждого склада сделать правильный учет за первый раз, что привело к повышению точности учета на всех складах.
Как аналитик убедил руководство в жизнеспособности предложенного порога безубыточности для повторного переучета?
3. В аэрофлоте рабочие часы устанавливаются в соответствии с договорами, заключенными с профсоюзными организациями. В частности, максимальная продолжительность работы может быть ограничена 16 часами для полетов на Боинге-74719 (В-747) и 14 часами — на Боинге-707 (В-707). Если эти пределы превышаются в силу неожиданных задержек, экипаж должен быть заменен новым. Аэрофлот содержит резервные экипажи для таких случаев. Средняя годовая стоимость содержания член» резервного экипажа оценивается в 30 000 долларов. Задержка полета на одну ночь, обусловленная отсутствием резервного экипажа, может стоить 50 000 долларов. Член экипажа находится по вызову непрерывно 12 часов в сутки 4 дня в неделю и может находиться по вызову три оставшихся дня недели. Самолет В-747 может обслуживаться двумя экипажами для самолета В-707.
Следующая таблица содержит вероятности вызова резервных экипажей, вычисленные на основании трехлетнего опыта.
| Категория рейса | Рейс (время вылета) | Вероятность вызова | |
| В – 747 | В – 707 | ||
| 14.0 | 0.014 | 0.072 | |
| 13.0 | 0.000 | 0.019 | |
| 12.5 | 0.000 | 0.006 | |
| 12.0 | 0.016 | 0.006 | |
| 11.5 | 0.003 | 0.003 | |
| 11.0 | 0.002 | 0.003 |
Приведённые данные свидетельствуют, например, что для 14-часового рейса вероятность вызова равна 0.014 для В-747 и 0.072— для В-707.
Типичная пиковая часть расписания дня имеет следующий вид.
| Время дня | Самолет | Категория рейса |
| 8:00 | ||
| 9:00 | ||
| 10:00 | ||
| 11:00 | ||
| 15:00 | ||
| 16:00 | ||
| 19:00 |
Существующая политика относительно резервных экипажей состоит в использовании двух экипажей (по семь членов каждый) от 5:00 до 11:00, четырех — от 11:00 до 17:00 и двух — от 17:00 до 23:00.
Оцените эффективность Существующей политики относительно резервных экипажей. В частности, является ли число резервных экипажей очень большим, очень малым или таким, как необходимо?
[1] Экстремальные величины всегда существуют вследствие того, что функция является непрерывной на замкнутом множестве
, , , .
Дата: 2016-10-02, просмотров: 507.