Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Действия игрока А

1-й шаг. В каждой строке матрицы А ищется минимальный элемент

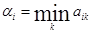, i = 1, 2, … , m.

Полученные числа

α₁, α_{2, …} , α_m

приписываются к заданной таблице в виде правого добавочного столбца

a11	a12	…	a1n	α1
a21	a22	…	a2n	α2
…	…	…	…	…
am1	am2	…	amn	αm

 

Пояснение. Выбирая стратегию А_i, игрок А вправе рассчитывать на то, что в результате разумных действий противника (игрока В) он выиграет не меньше чем а_i.

2-й шаг. Среди чисел

α₁, α_{2, …} , α_m

выбирается максимальное число

или, подробнее,

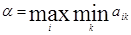
Специально отметим, что выбранное число α является одним из элементов заданной матрицы А.

Пояснение. Действуя наиболее осторожно и рассчитывая на наиболее разумное поведение противника, игрок А должен остановиться на той стратегии A_i, для которой число а_i, является максимальным.

Если игрок А будет придерживаться стратегии, Выбранной описанным выше спосо­бом, то при любом поведении игрока В игроку А гарантирован выигрыш, не меньший α.

Число α называется нижней ценой игры.

Принцип построения стратегии игрока А, основанный на максимизации минимальных выигрышей, называется принципом максимина, а выбираемая в соответствии с этим принципом стратегия А_i⁰ — максиминной стратегией игрока А.

 

Действия игрока В

1 шаг. В каждом столбце матрицы А ищется максимальный элемент

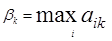, k = 1, 2, … , n.

Полученные числа

β₁, β₂, … , β_n

приписываются к заданной таблице в виде нижней добавочной строки

a11	a12	…	a1n	α1
a11	a22	…	a2n	α2
…	…	…	…	…
a11	am2	…	amn	αm
β1	β2	…	βn

Пояснение. Выбирая стратегию В_k, игрок В должен рассчитывать на то, что в результате разумных действий противника (игрока А) он проиграет не больше чем β_k.

2-й шаг. Среди чисел

β₁, β₂, … , β_n

выбирается минимальное число

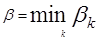
или, подробнее,

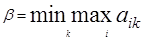
Выбранное число β также является одним из элементов заданной матрицы А.

 

Пояснение. Действуя наиболее осторожно и рассчитывая на наиболее разумное поведение противника, игрок В должен остановиться на той стратегии В_k*, для которой число β_k является минимальным.

 

Если игрок В будет придерживаться стратегии, выбранной описанным выше способом, то при любом поведении игрока А игроку В гарантирован проигрыш, не боль­
ший β.

Число β называется верхней ценой игры.

Принцип построения стратегии игрока B, основанный на минимизации максимальных потерь, называется принципом минимакса, а выбираемая в соответствии с этим принципом стратегия B_k⁰ – минимаксной стратегией игрока В.

Нижняя цена игры α и верхняя цена игры β всегда связаны неравенством

 

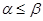
Замечание. Реализация описанного алгоритма требует 2mn - 1 сравнений элементов матрицы А:

(n - 1)m + m - 1 = mn - 1

сравнений для определения α,

(n - 1)m + m - 1 = mn - 1

сравнений для определения β и одно сравнение полученных чисел α и β.

 

Если

,

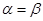или, подробнее,

,

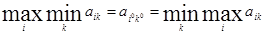то ситуация {А_i⁰, В_k⁰} оказывается равновесной, и ни один из игроков не заинтересован в том, чтобы ее нарушить (в этом нетрудно убедиться путем рассуждений, подобных проведенным при анализе игры в примере 2).

В том случае, когда нижняя цена игры равна верхней цене игры, их общее значение называется просто ценой игры и обозначается через ν.

Цена игры совпадает с элементом 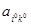матрицы игры А, расположенным на пересечении i⁰-й строки (стратегия 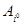игрока А) и k⁰-го столбца (стратегия 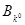игрока В) – минимальный в своей строке и максимальный в своем столбце.

Этот элемент называют седловой точкой матрицы А, или точкой равновесия, а про игру говорят, что она имеет седловую точку.

Стратеги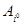и и 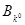, соответствующие седловой точке, называются оптимальными, а совокупность оптимальных ситуаций и цена игры – решением матричной игры с седловой точкой.

 

Замечание. Седловых точек в матричной игре может быть несколько, но все они имеют одно и то же значение.

 

Матричные игры с седловой точкой важны и интересны, однако более типичным является случай, когда применение описанного алгоритма приводит к неравенству

.

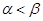Как показывает следующий пример, в этом случае предложенный выбор стратегий уже, вообще говоря, к равновесной ситуации не приводит, и при многократном ее повторении у игроков вполне могут возникнуть мотивы к нарушению рекомендаций, основанных на описанном алгоритме действий игроков А и В.

Пример 3. Рассмотрим 3 x 3 игру, заданную матрицей

.

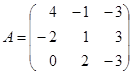Применив предложенный алгоритм

		-3	-3
-2			-2
		-3	-3

 

находим нижнюю цену игры α = -2 и соответствующую ей стратегию А₂, верхнюю цену игры β = 2 и соответствующую ей стратегию B₂.

Нетрудно убедиться в том, что пока игроки придерживаются этих стратегий, средний выигрыш при многократном повторений игры равен 1. Он больше нижней мены игры, но меньше верхней цены.

Однако если игроку В станет известно, что игрок А придерживается стратегии А₂, он немедленно ответит стратегией В₁ и сведет его выигрыш к проигрышу -2. В свою очередь, на стратегию В₁ у игрока А имеется ответная стратегия А₁, дающая ему выигрыш 4.

Тем самым, ситуация { А₂, В₂} равновесной не является.

 

 

Смешанные стратегии

В случае, когда нижняя цена игры α и верхняя цена игры β не совпадают,

,

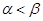игрок А может обеспечить себе выигрыш, не меньший α, а игрок В имеет возможность
не дать ему больше, чем β. Возникает вопрос – а как разделить между игроками разность

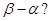
Предыдущие построения на этот вопрос ответа не дают — тесны рамки возможных действий игроков. Поэтому довольно ясно, что механизм, обеспечивающий полу­чение каждым из игроков как можно большей доли этой разности, следует искать в определенном расширении стратегических возможностей, имеющихся у игроков изначально.

Оказывается, что компромиссного распределения разности между игроками и уверенного получения каждым игроком своей доли при многократном повторении игры можно достичь путем случайного применения ими своих первоначальных, чи­стых стратегий. При таких действиях

– во-первых, обеспечивается наибольшая скрытность выбора стратегии (результат выбора не может стать известным противнику, поскольку он неизвестен самомуигроку),

– во-вторых, при разумном построении механизма случайного выбора стратегий, последние оказываются оптимальными.

Случайная величина, значениями которой являются стратегии игрока, называется его смешанной стратегией.

Тем самым, задание смешанной стратегии игрока состоит в указании тех вероятностей, с которыми выбираются его первоначальные стратегии.

 

 

Основные определения

Рассмотрим произвольную m х n игру, заданную m х n-матрицей

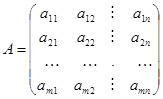
Так как игрок А имеет m чистых стратегий, то его смешанная стратегия может, быть описана набором m неотрицательных чисел

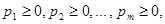
сумма которых равна 1,

.

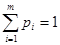Смешанная стратегия второго игрока В, имеющего п чистых стратегий, описыва­ется набором п неотрицательных чисел

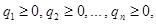
сумма которых равна 1,

.

 

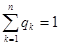Замечание. Каждая чистая стратегия является частным случаем смешанной стратегии: в частности, чистая стратегия A_i является смешанной стратегией, описываемой набором чисел Рев котором p₁, p₂, … , p_m, в котором

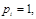
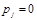
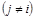
Подчеркнем, что для соблюдения секретности каждый из игроков применяет свои стратегии независимо от другого игрока.

Таким образом, задав два набора

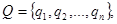
мы оказываемся в ситуации в смешанных стратегиях. В этих условиях каждая обычная ситуация (в чистых стратегиях) {А_i, B_k} по определению является случайным событием и, ввиду независимости наборов Р и Q, реализуется с вероятностью p_iq_k. В этой ситуации {А_i, B_k} игрок А получает выигрыш a_ik. Тем самым, математическое ожидание выигрыша игрока А в условиях ситуации в смешанных стратегиях (Р, Q) равно

.

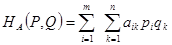Это число и принимается за средний выигрыш игрока А при смешанных стратегиях

 

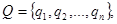
Определение. Стратеги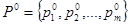и

и

называются оптимальными смешанными стратегиями игроков А и В соответственно, если выполнено следующее соотношение

.

 

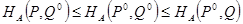Пояснение. Выписанные неравенства означают следующее:

левое неравенство – отклонение игрока А от оптимальной стратегии Р⁰ при условии, что игрок В придерживается стратегии Q⁰, приводит к тому, что выигрыш отклонившегося игрока А может только уменьшиться,

правое неравенство – отклонение игрока В от оптимальной стратегии Q⁰ при условии, что игрок А придерживается стратегии Р⁰, приводит к тому, что выигрыш игрока А может только возрасти, и значит, выигрыш игрока В – только уменьшиться.

 

Приведенное условие оптимальности равносильно тому, что[1]

Величина

,

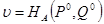определяемая последней формулой, называется ценой игры.

Набор (Р⁰, Q⁰, ν), состоящий из оптимальных смешанных стратегий игроков А и В и цены игры, называется решением матричной игры.

 

Пример 4. Рассмотрим 2 x 2 матричную игру из примера 1. Матрица этой игры имеет следующий вид

.

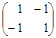Как нетрудно убедиться, седловой точки у нее нет.

Смешанные стратегии игроков А и В могут быть описаны парами чисел

P = {p, 1 - p} и Q = {q, 1 - q}

соответственно.

Средний выигрыш игрока А вычисляется так

?

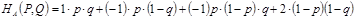откуда легко следует, что

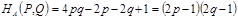
Последнее удобно записать так

.

 

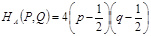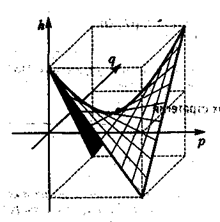
Рис. 1

Полученная формула показывает, что если игрок А в половине случаев записывает на листе бумаге четное (нечетное) число (выбирает р = 1/2), то независимо от того, что делает игрок В, ожидаемый (средний) вы­игрыш игрока А в каждой партии будет нулевым.

Если же игрок А выберет р > 1/2 (так что разность р-1/2 будет положительной), то узнав об этом, игрок В может выбрать q < 1/2 (так что разность q - 1/2 будет отрицательной) и, тем самым, сделать средний выигрыш игрока А отрицательным, то есть заставит его проиграть. Если же игрок А выберет р < 1/2 (так что разность р -1/2 будет отрицательной) и игрок В узнает об этом, то он может выбрать q > 1/2 (так что разность q -1/2 бу­дет положительной) и вновь сделать выигрыш игрока А отрицательным, то есть опять заставит его проиграть.

Исследуем теперь эту формулу с точки зрения игро­ка В.

Если игрок А выбирает р = 1/2, то ожидаемый (средний) выигрыш игрока B независимо от его дей­ствий будет нулевым в каждой партии. Но если игрок В выберет q > 1/2 (так что разность q - 1/2 будет положительной), то, узнав об этом, игрок А может выбрать р < 1/2 (так что разность р - 1/2 будет отри­цательной), и тогда игрок В будет проигрывать в каждой партии. Если же игрок В выберет q < 1/2 (так что разность q -1/2 будет отрицательной) и игрок А узнает об этом, то он может выбрать р > 1/2 (так что разность р -1/2 будет положительной) и вновь заставит игрока В проиграть.

Тем самым наборы

,

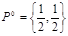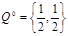
является оптимальными, а исход игры ничейным:

ν = 0.

Замечание. На рисунке 1 показано, как устроена поверхность, описываемая функцией

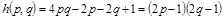
Точка

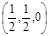
является седловой точкой (точкой перевала) этой поверхности. Именно эта точка и дает решение рассматриваемой матричной игры.

 

Естественно возникают два ключевых вопроса:

1-й – какие матричные игры имеют решение в смешанных стратегиях?

2-й – как находить решение матричной игры, если оно существует?

Ответы на эти вопросы дают следующие две теоремы.