Опишем метод отыскания решения матричной игры — цены игры и оптимальных смешанных стратегий, в известной степени верно отражающий некоторую реальную ситуацию накоплении опыта постепенной выработки игроками хороших стратегий в результате многих повторений конфликтных ситуаций. Основная идея этого метода заключается в том, чтобы мысленно как бы смоделировать реальное практическое «обучение» игроков в ходе самой игры, когда каждый из игроков на собственном опыте прощупывает способ поведения противника и старается отвечать на него наиболее выгодным для себя образом. Иными словами, всякий раз при возобновлении тигры игрок выбирает наиболее выгодную для себя стратегию, опираясь на предыдущий выбор противника.
Проиллюстрируем этот метод на примере игры, заданной матрицей
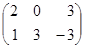
(здесь maxmin = 0, minmax = 2 → седловой точки нет).
Опишем правила выбора ходов игроками, предположив, для определенности, что начинает игрок А:
ход игрока А — стратегия А1 — (2 0 3);
игрок В выбирает свою стратегию так, чтобы выигрыш игрока А был минимален (отмечен полужирным шрифтом)
ход игрока В — стратегия В2 — 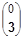
игрок А выбирает свою стратегию так, чтобы его выигрыш при стратегии B2 игрока В был максимален (отмечен полужирным шрифтом):
ход игрока А — стратегия А2 — (1 3 - 3);
игрок В выбирает свою стратегию так, чтобы «накопленный» выигрыш игрока А при стратегиях А1 и А2,
(2 0 3) + (1 3 -3) = (3 3 0),
был минимален:
ход игрока В — стратегия В3 — 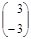 ;
;
игрок А выбирает свою стратегию так, чтобы его «накопленный» выигрыш при стратегиях B2 и B1 игрока В,
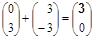
был максимален:
ход игрока А — стратегия А1 — (2 0 3);
игрок В выбирает свою стратегию так, чтобы «накопленный» выигрыш игрока А при стратегиях A1, A2 и A1,
(3 3 0) + (2 0 3) = (5 3 3),
был минимален:
ход игрока В — стратегия B2 — 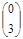
и т.д.
Разобьем последовательные ходы игроков А и В на пары
(ход игрока А, ход игрока В)
и запишем результаты в таблице
| n | i | B1 | B2 | B3 | ν*(n) | k | A1 | A2 | ν*(n) | ν(n) |
| 0,00 | 3,00 | 1,50 | ||||||||
| 0,00 | 1,50 | 0,75 | ||||||||
| 1,00 | 1,00 | 1,00 | ||||||||
| 0,75 | 1,50 | 1,12 | ||||||||
| 0,60 | 1,20 | 0,90 | ||||||||
| 1,00 | 1,00 | 1,00 | ||||||||
| 0,86 | 1,44 | 1,15 | ||||||||
| 0,75 | 1,13 | 0,93 | ||||||||
| 1,00 | 1,00 | 1,00 | ||||||||
| 0,90 | 1,20 | 1,05 | ||||||||
| 0,82 | 1,09 | 0,96 | ||||||||
| 1,00 | 1,00 | 1,00 | ||||||||
| ………………………………………………………………………………………………….. |
требующей некоторых пояснений.
Описание таблицы
| 1-й столбец | номер n шага (пары последовательных ходов игроков А и В) | |
| 2-й столбец | номер i стратегии, выбранной игроком А | |
| 3-й столбец | «накопленный» суммарный выигрыш игрока А за первые n шагов при стратегии В1 игрока В | Минимальный из этих выигрышей выделяется полужирным шрифтом |
| 4-й столбец | «накопленный» суммарный выигрыш игрока А за первые n шагов при стратегии В2 игрока В | |
| 5-й столбец | «накопленный» суммарный выигрыш игрока А за первые n шагов при стратегии В3 игрока В | |
| 6-й столбец | минимальный средний выигрыш игрока А, равный, минимальному накопленному им выигрышу за первые n шагов, деленному на число этих шагов | |
| 7-й столбец | номер k стратегии, выбранной игроком В | |
| 8-й столбец | «накопленный» суммарный выигрыш игрока А за первые n шагов при стратегии А1 | Максимальный из этих выигрышей выделяется полужирным шрифтом |
| 9-й столбец | «накопленный» суммарный выигрыш игрока А за первые n шагов при стратегии А2 | |
| 10-й столбец | максимальный средний выигрыш игрока А, равный максимальному накопленному им выигрышу за первые n шагов, деленному на число этих шагов | |
| 11-й столбец | среднее арифметическое минимального среднего выигрыша и максимального среднего выигрыша игрока A |
Решение игры определяется приближенно по окончании любого из шагов.
Например, за приближенную цену игры можно взять среднее арифметическое ν(n), полученное на n-м шаге. Смешанные стратегии противников определяются частотами появления чистых стратегий.
После 9-го шага имеем
ν(9) = l,00.
При этом игрок А 6 раз использовал стратегию А1 и 3 раза стратегию А2. В свое очередь игрок B 6 раз применял стратегию В2, 3 раза стратегию В3, а стратегией В1 не пользовался вообще. Отсюда получаем, что
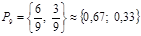 ,
, 
Соответственно, после 10-го шага получаем —
 .
.
Данная игра легко решается графически. Вот точный ответ:
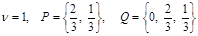 .
.
Сравнивая результаты, полученные на 9-м, 10-м, а также 11-м и 12-м шагах:
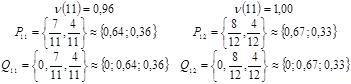
замечаем, что по мере увеличения числа шагов значения все меньше отличаются от точных.
Сделаем несколько замечаний.
Замечание 1. При увеличении числа шагов все три величины v*(n), v*(n) и v(n) будут приближаться к цене игры v, но среднее арифметическое v(n) будет приближаться к v сравнительно быстрее.
Замечание 2. Хотя сходимость итераций весьма медленна, тем не менее, даже такой небольшой расчет всегда дает возможность находить ориентировочное значение цены игры и доли чистых стратегий.
Замечание 3. Сравнительно медленная скорость сходимости можно объяснить целым рядом причин. Укажем одну из них, психологически наиболее интересную. Если, к примеру, игрок А уже получил оптимальную смешанную стратегию, то он не склонен останавливаться на ней. Отнюдь нет — он продолжит попытки выиграть у противника В побольше, особенно если последний еще не достиг оптимальной смешанной стратегии. Тем самым, игрок А может невольно ухудшить свое положение.
Замечание 4. Отметим два основных преимущества описанного метода:
1) итерационный метод прост и одновременно универсален (при его помощи можно легко найти приближенное решение любой матричной игры),
2) объем и сложность вычислений сравнительно слабо растут по мере увеличения числа стратегий игроков (размеров матрицы игры).
Дата: 2016-10-02, просмотров: 311.