Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Рассмотрим m x n игру с платежной матрицей

A = (a_ik).

Без ограничения общности будем считать, что все элементы матрицы А положительны (этого всегда можно добиться, пользуясь аффинным правилом, преобразую­щим заданную матрицу игры, но не изменяющим оптимальных смешанных стратегий игроков). Тем самым, искомая цена игры v — положительное число.

Интересы игрока А

Из теоремы о свойствах оптимальных смешанных стратегий игроков вытекает, что при любой чистой стратегии В_k игрока В, k = 1, 2, ... , n, оптимальная смешан­ная стратегия Р = {p₁, p₂, … , p_m} игрока А обеспечивает его средний выигрыш, не меньший v. Иными словами, выполняются соотношения

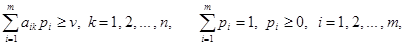
которые с учетом обозначений

можно записать так

Поскольку игрок А стремится сделать гарантированный выигрыш макси­мально возможным, то задача отыскания решения матричной игры сводится к следу­ющей задаче:

найти неотрицательные величины х₁, x₂, ... , х_m, удовлетворяющие неравенствам

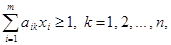
и такие, что их сумма минимальна

.

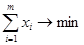Интересы игрока B

Аналогичным образом заключаем, что оптимальная смешанная стратегия Q = {q₁, q₂, … , q_n} игрока В при любой чистой Стратегии А₁ игрока A, i = 1, 2,... , m, обеспечивает его средний проигрыш, не больший v. Иными словами, выполняются соотно­шения

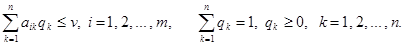
которые с учетом обозначений

можно записать так

Поскольку игрок В стремится сделать свой гарантированный проигрыш мини­мально возможным, то задача отыскания решения матричной игры сводится к следу­ющей задаче:

найти неотрицательные величины у₁,у₂, ... , у_n, удовлетворяющие неравенствам

и такие, что их сумма максимальна

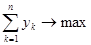
Тем самым, мы получаем следующий важный результат.

Теорема 3. Решение матричной игры с положительной платежной матрицей (а_ik) равно­сильно решению двойственных задач линейного программирования

(A) ,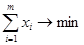

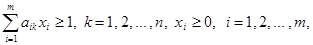
(B) ,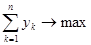

При этом цена игры

,

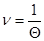где Θ — величина, обратная общему значению оптимальных сумм,

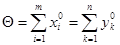
а оптимальные значения 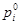и 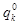связаны с оптимальным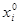и и 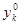посредством равенств

 

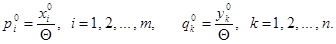
Алгоритм решения матричной игры

1-й шаг. Ко всем элементам исходной матрицы игры прибавляется одно и то же положительное число γ так, чтобы все элементы новой матрицы были строго положи­тельны.

2-й шаг. Решаются двойственные задачи линейного программирования (А) и (В) (например, симплекс-методом, или как-нибудь иначе). Находятся наборы 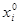, 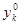и число Θ.

3-й шаг. Строятся оптимальные смешанные стратегии игроков А и В соответствен­но

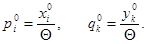
4-й шаг. Вычисляется цена игры

 

Пример 9. Рассмотрим 2 x 2 игру с матрицей

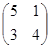
Соответствующие ей задачи линейного программирования имеют вид

 

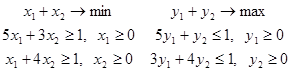
Решение.

1-й шаг. Все элементы платежной матрицы положительны.

2-й шаг. Строим решения обеих задач линейного программирования, пользуясь графическим ме­тодом. В результате получаем, что

Й шаг.

4-й шаг.

 

Примеры задач, сводимых к матричным играм

 

В чистом виде антагонистические конфликты встречаются редко (разве только в бо­евых действиях и в спортивных состязаниях). Однако довольно часто конфликты» в которых интересы сторон противоположны, при допущении, что множество спосо­бов действия сторон конечно, можно моделировать матричными играми.

Рассмотрим несколько конкретных ситуаций.

Пример 10. «Планирование поема». Сельскохозяйственное предприятие имеет возможность выращивать две культуры — А₁ и А₂. Необходимо определить, как сеять эти культуры, если при прочих равных, условиях их урожаи зависят от погоды, а план посева должен обеспечить наибольший доход (прибыль от реализации выращенной культуры определяется полученным объемом). В зоне рискованного земле­делия (а таковой является большая часть России) планирование посева должно осуществляться с учетом наименее благоприятного состояния погоды.

Таким образом, одной из сторон выступает сельскохозяйственное предприятие, заинтересованное в том, чтобы получить наибольший доход (игрок А), а другой стороной — природа, способная навредить сельскохозяйственному предприятию в максимальной степени (от нее зависят погодные условия) и преследующая тем самым прямо противоположные цели (игрок В).

Принятие природы за противника равносильно планированию посева с учетом наиболее небла­гоприятных условий; если же погодные условия окажутся благоприятными, то выбранный план даст возможность увеличить доход.

Налицо антагонистический конфликт, в котором у игрока А две стратегии — А₁ и А₂, а у игрока В три — В₁ (засушливое лето), В₂ (нормальное лето) и В₃ (дождливое лето).

В качестве выигрыша игрока А возьмем прибыль от реализации и будем считать, что расчеты прибыли сельскохозяйственного предприятия (в млрд руб.) в зависимости от состояний погоды сведены в следующую матрицу

.

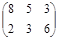Нетрудно заметить, что седловой точки у этой матрицы нет. Поэтому оптимальная стратегия игрока А будет смешанной. Применяя графический метод, получаем

.

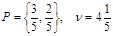Замечание. Здесь мы столкнулись со сравнительно редкой ситуацией, когда оптимальная смешан­ная стратегия одного из игроков допускает так называемую «физическую» реализацию. Полученное решение сельскохозяйственное предприятие может использовать так:

на 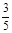всех площадей выращивать культуру А₁,

на всех площадей выращивать культуру A₂

и получать прибыль в размере, не меньшем 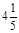млрд руб.

 

Пример 11. «Переговоры о заключении контракта между профсоюзом и администрацией». Рассмотрим фир­му, администрация которой ведет переговоры с профсоюзом рабочих и служащих о заключении кон­тракта.

Предположим, что платежная матрица, отражающая интересы договаривающихся сторон, имеет следующий вид

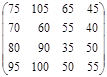
Выплаты указаны в центах в час и представляют собой среднюю зарплату служащего фирмы вместе со всеми добавками. Тем самым, заданная матрица описывает прибыль профсоюза (игрок А) и затраты администрации фирмы (игрок В).

Ясно, что профсоюз стремится максимизировать доходы рабочих и служащих, в то время как ад­министрации хотелось бы минимизировать собственные потери.

Нетрудно заметить, что седловой точки у платежной матрицы нет. Кроме того, для дальнейшего анализа существенными являются лишь стратегии А₁ и А₄ игрока А и стратегии В₃ и В₄ игрока В (в этом нетрудно убедиться, воспользовавшись правилом доминирования стратегий). В результате со­ответствующего усечения получим матрицу

.

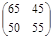Элементы матрицы

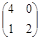
связаны с элементами предыдущей матрицы соотношениями

65 + 5 х 4 + 45, 45 = 5 х 4 + 45, 50 = 5 х 1 + 45, 55 = 5 х 2 +45.

Воспользовавшись графическим методом, в итоге получим

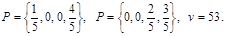
Тем самым, профсоюзу следует выбирать стратегию А₁ в 20 % случаев и стратегию А₄ в 80 %. Что касается администрации, то ей следует выбирать стратегию В₃ с вероятностью 0,4 и стратегию В₄ с вероятностью 0,6. При этом ожидаемая цена игры равна 53.

Замечание. Следует отметить, что если процесс переговоров будет повторяться много раз, то среднему должно сходиться к ожидаемому значению 53. Если же переговоры пройдут лишь единожды, то ре­альный результат подучится при выборе каждым игроком некоторой своей чистой стратегии. Поэтому один из игроков, профсоюз или администрация, будет неудовлетворен.

 

Пример 12. «Локальный конфликт». Рассмотрим войну между двумя небольшими государствами А и В, которая ведется в течение 30 дней.

Для бомбардировки небольшого моста — важного военного объекта страны В — страна А исполь­зует оба имеющихся у нее самолета. Разрушенный мост восстанавливается в течение суток, а каждый самолет совершает один полет в день по одному из двух воздушных маршрутов, соединяющих эти стра­ны. У страны В есть два зенитных орудия, при помощи которых можно сбивать самолеты страны А. Если самолет собьют, то некая третья страна в течение суток поставит стране А новый самолет.

Страна А может послать самолеты либо по одному маршруту, либо по разным. Страна В может поместить либо обе зенитки на одном маршруте, либо по одной зенитке на каждый маршрут.

Если один самолет летит по маршруту, на котором расположена одна зенитка, то этот самолет бу­дет сбит. Если два самолета летят по маршруту, на котором расположены две зенитки, то оба самолета будут сбиты. Если два самолета летят по маршруту, на котором расположена одна зенитка, то сбит будет только один самолет. Если самолет доберется до цели, то мост будет уничтожен.

У страны А есть две стратегии:

послать самолеты по разным маршрутам — А₁,

послать самолеты по одному маршруту — А₂.

У страны В — также две стратегии:

поместить зенитки на разных маршрутах — В₁,

поместить зенитки на одном маршруте — В₂.

Если страна А выберет стратегию А₁, а страна В — стратегию В₁, то страна А получит нулевой выигрыш, так как ни один из самолетов не достигнет цели.

Если страна А выберет стратегию А₂, а страна В — стратегию В₁, то хота бы один самолет достигнет цели и вероятность разрушения моста будет равна 1.

Если страна А выберет стратегию А₁, а страна В — стратегию В₂, то вновь хотя бы один самолет достигнет цели и вероятность разрушения моста будет равна 1.

Если страна А выберет стратегию А₂, а страна В — стратегию В₂, то страна А с вероятно­стью 1/2 выберет маршрут, на котором установлены зенитки, и, следовательно, цель будет уничтожена с вероятностью 1/2.

Оформим результаты проведенного анализа в стандартной игровой форме:

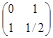
При помощи графического метода получаем оптимальные смешанные стратегии игроков и цену игры

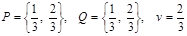
Это означает, что если страна А будет посылать самолеты по разным маршрутам в течение десяти дней из тридцати, отпущенных на войну (и, значит, по одному маршруту в течение двадцати дней), то в среднем страна А будет иметь 66,7 % удачных случаев (мост будем находиться в нерабочем состо­янии). Воспользовавшись для своих зениток предложенным выбором, страна В не позволит бомбить мост чаще, чем в 66,7 % случаев.

 

 

Несколько слов в заключение

Матричные игры моделируют конфликтные ситуации, в которых каждая из сторон-участниц делает свой ход одновременно со второй стороной. При этом наибольший интерес представляет случай, когда игра не заканчивается сразу же после совершения игроками одной такой пары одновременных ходов, а повторяется многократно. При­чем считается, что перед каждым возобновлением игры игроки не получают никаких новых сведений ни о конфликте, ни о возможных действиях противной стороны. Ины­ми словами, при многократном повторении матричной игры каждая из сторон всякий раз оказывается перед выбором некоторой стратегии из одного и того же множества стратегий, неизменного у каждого из игроков.

Тем не менее, в таких многократно повторяющихся обстоятельствах большую роль играет анализ игры, как предварительный, так и промежуточный.

В результате разумно проведенного предварительного анализа матричной игры заинтересованная в анализе сторона может определить свою линию поведения (правило выбора стратегий) на всю серию игр. Разумеется, описанный нами выше максиминный подход является далеко не единственным средством. Однако не следует забы­вать, что принципиальной особенностью этого подхода является то обстоятельство, что игрок, придерживающийся выводимого на его основе правила выбора стратегий, заранее может довольно точно оценить нетривиальные размеры своего гарантирован­ного выигрыша. Кроме того, максиминный подход позволяет сводить задачу поиска решения игры к рассмотрению сравнительно несложных задач линейного програм­мирования и, тем самым, получать эффективные рекомендации по тому, как лучше выбирать стратегии в конкретной игре при многократном ее повторении.

Если игра повторяется много раз, то некоторые дополнительные сведения — какие именно стратегии выбирает противная сторона и какими правилами выбора стратегий она руководствуется — игрок все же получает. На основании этих сведений и резуль­татов предварительного анализа игры он может довольно точно оценить противника и, если тот не придерживается компромиссного максиминного подхода, внести соот­ветствующие изменения в собственную линию поведения и увеличить выигрыш.

 

О классификации игр

Реальные конфликтные ситуации приводят к различным видам игр. К настоящему времени общепризнанной классификации игр пока не сложилось. Тем не менее, легко заметить, что игры различаются по целому ряду признаков: по количеству участвующих в них игроков, по количеству возможных стратегий, по характеру взаимоотношений между игроками, по характеру выигрышей, по виду функций выигрышей, по количеству ходов, по характеру информационной обеспеченности игроков и т. д.

Остановимся на этих различиях чуть подробнее.

В зависимости от количества игроков определяют игры трех типов: игры одного игрока (в теории игр, как правило, не рассматриваются), игры двух игроков (наиболее изученный класс игр) и игры n игроков (успехов в изучении которых сравнительно немного вследствие возникающих принципиальных трудностей).

По количеству стратегий игроков игры делятся на конечные (каждый из игроков имеет конечное число возможных стратегий) и бесконечные (где хотя бы один из игроков имеет бесконечное количество возможных стратегий).

По характеру взаимоотношений между игроками игры делятся на бескоалиционные (в которых игроки не имеют права вступать в соглашения и образовывать коалиции), коалиционные (в которых игроки могут вступать в соглашения и образовывать коа­лиции) и кооперативные (в которых соглашения, связывающие игроков, определены наперед и обязательны):

По характеру выигрышей различают игры с нулевой суммой (общий капитал игроков не изменяется, а просто перераспределяется между игроками в зависимости от полу­чающихся исходов) и игры с ненулевой суммой.

Игру двух игроков с нулевой суммой часто называют антагонистической, вслед­ствие того, что цели игроков в них прямо противоположны: выигрыш одного из игро­ков происходит только за счет проигрыша другого.

По виду функций выигрышей игры делятся на: матричные игры (рассмотренные выше), биматричные игры, игры типа дуэлей, непрерывные игры, выпуклые игры и др.

По количеству ходов игры делятся на одношаговые (завершающиеся после одного хода каждого из игроков) и многошаговые, которые, в свою очередь, делятся на позици­онные игры (каждый из игроков может последовательно во времени делать несколько ходов), стохастические игры (где при выборе новых позиций имеется определенная вероятность возврата на предшествующую позицию), дифференциальные игры (в кото­рых допускается делать ходы непрерывно и подчинять поведение игроков условиями, описываемыми дифференциальными уравнениями), игры типа дуэлей (характеризу­ющиеся моментом выбора хода и вероятностями получения выигрышей в зависимости от времени, прошедшего от начала игры до момента выбора).

По характеру информационной обеспеченности игроков различают игры с полной информацией (на каждом ходе игры каждому игроку известно, какие выборы были сделаны ранее всеми игроками) и игры с неполной информацией (если в игре не все известно о предыдущих выборах).

Существуют, разумеется, и другие виды игр.

В зависимости от вида игры разрабатывается и метод ее решения. Однако читатель, видимо, уже заметил, что структура предложенного выше описания основных напра­влений различения игр не является древовидной: одни и те же виды игр оказываются в разных классах.

Впрочем, возможны и иные подходы к разбиению игр.

Далее мы рассмотрим некоторые из указанных видов игр, а именно позиционные и биматричные игры.

 

Часть II ПОЗИЦИОННЫЕ ИГРЫ

 

Во многих практически важных конфликтных ситуациях, располагая той или иной информацией об их прошлом развитии, стороны-участницы совершают свой выбор не раз и навсегда, а последовательно во времени, шаг за шагом. Тем самым, они используют стратегии, отражающие как динамику конфликта, так и степень собствен­ной информированности о фактически складывающейся обстановке в развитии этого конфликта.

 

Структура позиционной игры

Одним из классов игр, описывающих конфликты, динамика которых оказывает влияние на поведение участников, являются так называемые позиционные игры.

Позиционная игра — это бескоалиционная иг­ра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и, вообще говоря, неполной информации.

Процесс самой игры состоит в последователь­ном переходе от одного состояния игры к дру­гому состоянию, который осуществляется либо путем выбора игроками одного из возможных действий в соответствии с правилами игры, ли­бо случайным образом (случайный ход).

В качестве примеров позиционных игр мож­но привести крестики-нолики, шашки, шахматы, карточные игры, домино и др. Интересно, что право выбора первого хода в этих играх часто определяется случайным образом.

Состояния игры принято называть позициями (отсюда и название — позиционные игры), а возможные выборы в каждой позиции — альтернативами.

Характерной особенностью позиционной игры является возможность представления множества позиций в виде древовидного упорядоченного множества, которое называется деревом игры (рис. 1).

Для определенности мы будем рассматривать позиционные игры, в каждой пози­ции которых, кроме окончательных, ровно две альтернативы — первая и вторая.

Замечание. Символ О, А или В в кружке указывает, кто из игроков (О, А или В) делает очередной ход в заданной позиции. При этом символом О обычно обозначается ход в игре, осуществляемый не игроком, а каким-нибудь случайным механизмом (иногда его называют природой). Например, в позиционной игре, представленной на рис. 1 своим деревом, первый ход производится случайно.

Пользуясь графическим описанием игры, можно сказать, что процесс игры состоит в переходе от начальной позиции к окончательной через непосредственно следующие одна за другой промежуточные позиции.

Каждая окончательная вершина определяет единственную цепь (последовательность идущих друг за другом звеньев), связывающую начальную вершину с данной (рис. 2). Такая цепь называется партией. На рис. 2 одна из партий выделена жирными линиями. Число различных партий равно числу окончательных вершин (позиций).

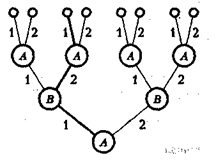
Рис. 2

В каждой окончательной позиции задан числовой выигрыш игрока А.

Замечание. Мы будем рассматривать здесь только антагонистические позиционные игры.

В шахматах функция выигрышей игрока А (белых) определяется так:

+1 на выигрываемых партиях,

0 на ничейных партиях,

-1 на проигрываемых партиях.

Функция выигрышей игрока В (черных) отличается от функции выигрышей белых только знаком.

Различают позиционные игры с полной информацией и позиционные игры с неполной информацией.

В позиционных играх с полной информацией (пример — шашки, шахматы) каждый игрок при своем ходе знает ту позицию дерева игры, в которой он находится.

В позиционных играх с неполной информацией (пример — домино) игрок, де­
лающий ход, не знает точно, в какой именно позиции дерева игры он фактически
находится. Этому игроку известно лишь некоторое множество позиций, включающее
в себя его фактическую позицию. Такое множество позиций называется информационным множеством.

Таким образом, в игре с неполной информацией игрок при своем ходе знает, в каком информационном множестве он находится, но ему неизвестно, в какой именно позиции этого множества.

Позиции, принадлежащие одному и тому же информационному множеству, объединяются пунктирными линиями.

Рассмотрим примеры двух игр, состоящих из двух ходов, которые последовательно делают участвующие в ней игроки А и В. Начинает игрок А: он выбирает одну из двух возможных альтернатив — число х, равное либо 1 (первая альтернатива), либо 2 (вторая альтернатива). На ход игрока А игрок В отвечает своим ходом, выбирая одну из двух возможных альтернатив — число у, равное либо 1 (первая альтернатива), либо 2 (вторая альтернатива).

И в результате игрок А получает вознаграждение или вынужден платить штраф.

Пример 13.

1-й ход. Игрок А выбирает число х из множества двух чисел {1, 2}.

2-й ход. Игрок В выбирает число у из множества двух чисел {1,2}, зная выбор числа х игро­ком А.

Функция W(x, у) выплат игроку А за счет игрока В задается так

W(l, l) = 1, W(2, l) = -2,

W(l, 2) = -l, W(2, 2)= 2.

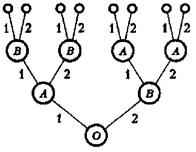
На рис. 3 показаны дерево игры и информационные множества.

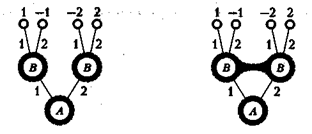
Рис. 3 Рис.4

Пример 14. В случав, вели выполнены все условия предыдущего примера, кроме одного — хода игро­ка В.

2-й ход — игрок В выбирает число у из множества двух чисел {1, 2}, не зная выбора числа х игроком А, информационные множества выглядят так, как показано на рис. 4.