Позиционная игра называется игрой с полной информацией, если в каждой позиции любой ее партии игрок, делающий ход, знает, какие альтернативы были выбраны на предыдущих ходах. В графическом описании каждая вершина дерева такой игры представляет собой отдельное информационное множество.
Примерами позиционных игр с полной информацией могут служить крестики-нолики, шашки и шахматы.
Основная особенность позиционной игры с полной информацией состоит в том, что соответствующая ей матрица выигрышей всегда имеет седловую точку, то есть в игре с полной информацией существуют оптимальные чистые стратегии и, значит, равновесная ситуация.
Сказанное означает, что в шахматах (крестиках-ноликах, шашках) уже в начальной позиции либо имеется способ выигрыша за белых, либо способ выигрыша за черных, либо как та, так и другая сторона способна форсировать ничью.
Однако известное доказательство существования равновесной ситуации неконструктивно и не дает эффективных приемов фактического нахождения решения игры.
И такие способы (стратегии) в шахматах не найдены до сих пор, и даже неизвестно, какая из перечисленных возможностей имеет место на самом деле.
Иное дело с игрой крестики-нолики: стратегий в ней немного и она разобрана до самого конца — существуют оптимальные чистые стратегии, ведущие игроков к ничьей.
Рассмотрим несколько примеров.
1. Как нетрудно заметить, двухходовая игра из примера 11 является игрой с полной информацией. Ее нормализация приводит к матрице с седловой точкой (см. пример 13).
2. «Выкладывание монет на стол». Два игрока поочередно кладут монеты одинаковых размеров на обыкновенный стол, всякий раз выбирая произвольное доступное место для монеты (взаимное накрывание монет не допускается). Тот из игроков, кто положит монету, не оставляющую места для новых монет, выигрывает.
Это игра с полной информацией. Существует вполне определенная стратегия, обеспечивающая выигрыш тому из игроков, кто начинает игру. А именно, начинающий игру должен положить первую монету точно в центр стола и на каждый ход противника отвечать симметричным ходом. Исход игры от стратегии второго игрока не зависит.
3. «Переговоры». В переговорах участвуют две стороны А и В. В слегка идеализированном варианте это может выглядеть, например, так.
Сначала сторона А высказывает одно из нескольких предложений, способных заинтересовать сторону В. Затем сторона В, ознакомившись с предложением стороны А, высказывает одно из нескольких встречных предложений, способных, по ее мнению, заинтересовать сторону А. В свою очередь, сторона А, ознакомившись с реакцией стороны В на сделанные предложения, высказывает ей новое предложение, внеся одну из нескольких возможных корректировок в свое первоначальное предложение с учетом мнения стороны В и т.д.
Если предмет переговоров сложен, то подобный обмен ходов может затянуться. Однако любые переговоры непременно заканчиваются. И там, на финише, ждет функция выигрышей.
Попробуем смоделировать короткий переговорный процесс трехходовой позиционной игрой.
Предположим, что переговоры заканчиваются через три хода, на каждом из которых соответствующая сторона имеет возможность выбора из двух альтернатив, и опишем соответствующую позиционную игру.
1-й ход делает сторона А: она выбирает одно из двух возможных предложений — число х из множества двух чисел {1, 2}.
2-й ход делает сторона В: она выбирает число у из множества двух чисел {1, 2}, зная число х, предложенное стороной А.
3-й ход делает сторона А: она выбирает число z из множества двух чисел {1, 2}, зная о предложении стороны В на 2-м ходе и помня собственное предложение на 1-м ходе.
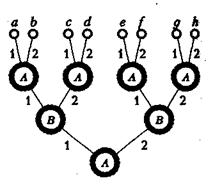
Рис. 11
После этого сторона А либо получает вознаграждение (например, в виде кредита от стороны В), либо выплачивает стороне В штраф.
Все эти возможности описываются функцией выигрышей W(x, у, z), заданной следующей таблицей
W(1, 1, 1) = a W(2, 1, 1) = e
W(1, 1, 2) = b W(2, 1, 2) = f
W(1, 2, 1) = c W(2, 2, 1) = g
W(1, 2, 2) = d W(2, 2, 2) = h.
Графическое представление этой игры показано на рис. 11.
Ясно, что описанная позиционная игра является игрой с полной информацией.
Начнем с описания возможных стратегий игрока В.
Поскольку игроку В выбор игрока А на 1-м ходе известен, то у игрока В те же четыре стратегии, что и в примере 13:
В1 – [1, 1], В2 – [1, 2], В3 – [2, 1], В4 – [2, 2],
С описания возможных стратегий игрока А дело обстоит немного посложнее — их восемь.
Чистая стратегия игрока А в данной игре описывается упорядоченной тройкой
(x, [z1, z2]).
Здесь x (x = 1, 2) — альтернатива, которую игрок А выбирает на 1-м ходе, z1 (z1 = 1, 2)— альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал первую альтернативу (у = 1) и z2 (z2 = 1, 2) — альтернатива, которую игрок А выбирает на 3-м ходе, если на 2-м ходе игрок В выбрал вторую альтернативу (у = 2).
Например, выбор игроком А стратегии (1, (2, 1]) означает, что на 1-м ходе игрок А выбирает х = 1, а на 3-м z = 2. если игрок В выбрал у = 1, и z = 1, если игрок В выбрал у = 2.
Тем самым, у игрока А восемь чистых стратегий:
A1 — (1, [1, 1]), A2 — (1, [1, 2]), A3 — (1, [2, 1]), A4 — (1, [2, 2]),
A5 — (2, [1, 1]), A6 — (2, [1, 2]), A7 — (2, [2, 1]), A8 — (2, [2, 2]),
Покажем теперь, как в зависимости от применяемых стратегий определяются элементы таблицы выигрышей игрока А.
Пусть, например, игрок А выбрал стратегию A6 — (2, [1, 2]), а игрок В — стратегию В3 – [2, 1]. Тогда х = 2. Из [2, 1] вытекает, что у = 1, а из (2, [1, 2]), что z = 1. Отсюда
W(x, y, z) = W(2, l, 1) = е.
Рассчитывая по этой же схеме все остальные элементы таблицы выигрышей, в итоге получим
| В1 | В2 | В3 | В4 | ||
| [1, 1] | [1, 2] | [2, 1] | [2, 2] | ||
| А1 | (1, [1, 1]) | W(1, 1, 1) | W(1, 1, 1) | W(1, 2, 1) | W(1, 2, 1) |
| А2 | (1, [1, 2]) | W(1, 1, 1) | W(1, 1, 1) | W(1, 2, 2) | W(1, 2, 2) |
| А3 | (1, [2, 1]) | W(1, 1, 2) | W(1, 1, 2) | W(1, 2, 1) | W(1, 2, 1) |
| А4 | (1, [2, 2]) | W(1, 1, 2) | W(1, 1, 2) | W(1, 2, 2) | W(1, 2, 2) |
| А5 | (2, [1, 1]) | W(2, 1, 1) | W(2, 2, 1) | W(2, 1, 1) | W(2, 2, 1) |
| А6 | (2, [1, 2]) | W(2, 1, 1) | W(2, 2, 2) | W(2, 1, 1) | W(2, 2, 2) |
| А7 | (2, [2, 1]) | W(2, 1, 2) | W(2, 2, 1) | W(2, 1, 2) | W(2, 2, 1) |
| А8 | (2, [2, 2]) | W(2, 1, 2) | W(2, 2, 2) | W(2, 1, 2) | W(2, 2, 2) |
Вследствие того, что рассматриваемая позиционная игра является игрой с полной информацией, полученная матрица имеет седловую точку при любой функции выигрышей. В атом легко убедиться, произвольно выбирая значат» параметров а, b, c, d, е, f, g и h.
При увеличении числа ходов стратегии в позиционной игре с полной информацией строятся по аналогичной схеме.
Рассмотрим, например, четырехходовую позиционную игру.
1-й ход делает игрок А: он выбирает число х из множества двух чисел {1, 2}.
2-й ход делает игрок В: он выбирает число у из множества двух чисел {1, 2}, зная число х, выбранное игроком А на 1-м ходе.
3-й ход делает игрок А: он выбирает число z из множества двух чисел {1, 2}, зная число у, выбранное игроком В на 2-м ходе, и помня свой выбор числа х на 1-м ходе.
4-й ход делает игрок В: он выбирает число u из множества двух чисел {1, 2}, зная число z, выбранное игроком А на 3-м хода, помня свой выбор числа у на 2-м хода и зная выбор игрока А на 1-м ходе — число х.
После этого игроки А и В расплачиваются а соответствии с заданной функцией выигрышей W(x, y, z, u).
В этой игре стратегии у игрока А те же, что и в задаче, рассмотренной выше: каждая из них задается тройкой вида
(x, [z1, z2]),
и общее их число равно восьми.
Что касается стратегий игрока В, то в этой игре их шестнадцать и каждая из них задается четверкой вида
([y1, y2], [u1, u2]).
Матрица выигрышей игрока А в данной игре имеет размер 8 х 16. Покажем, как определяются ее элементы в зависимости от применяемых стратегий игроков.
Пусть, например, игрок А выбрал стратегию А' — (2, [2, 1]), а игрок В стратегию В' — ([2, 1], [1,2]). Тогда х = 1, у = 2, а z = 1. Из того, что [u1, u2] = [1, 2], получаем, что u = 1. Отсюда следует, что искомый элемент матрицы выплат равен
W(1, 2, 1, 1)
Остальные элементы матрицы вычисляются аналогично.
Так как эта позиционная игра также является игрой с полной информацией, то получаемая матрица будет иметь седловую точку.
Несколько слов в заключение
В рассмотренных примерах основное внимание было; уделено описанию процесса нормализации позиционной игры — построению дерева игры и информационных множеств, выработке стратегий игроков и вычислению элементов платежной матрицы. Следующий естественный шаг — отыскание цены игры и оптимальных стратегий игроков — проводится методами, о которых рассказывалось в главе, посвященной матричным играм.
Мы достаточно подробно остановились на позиционных играх двух лиц, где был: явно выражены интересы одного из игроков (игрока А). Следует, однако, иметь в вид] что в одних случаях интересы игрока В могут быть полностью противоположным интересам игрока А, в то время как в других вполне может оказаться, что то, что хорошо для одного игрока, не обязательно плохо для другого. Приведем два простых примера.
Пример А.
1-й ход. Игрок А выбирает число х из множества двух чисел {1, 2}.
2-й ход. Игрок В выбирает число у из множества двух чисел {1, 2}, зная выбор числа х игроком А.
Функции выплат игрокам А и В — WA(x, у) и WB(x, у) соответственно — задаются так:
WA (1, 1) = 1, WA (1, 2) = -1, WA (2, 1) = -2, WA (2, 2) = 2,
WB (1, 1) = 2, WB (1, 2)= 1, WB (2, 1) = 1, WB (2, 2) = 2.
Дерево игры показано на рис. 12. Исход игры зависит от того, каковы намерения игрока В — максимизировать свой выигрыш:
WB(x, у) → max,
или максимизировать свой относительный выигрыш:
WB(x, у) WA(x, у)- , у) → max.
В первом Случав это достигается так:
При x = 1 у = 1 и WB(1, 1) = 2 (WA (1, 1) = 1);
При x = 2 у = 2 и WB (2, 2) = 2 (WA (2, 2) = 2).
Во втором случае:
При x = 1 у = 2 и WB(1, 2) - WA (1, 2) = 1 – (-1) = 2);
При x = 2 у = 1 и WB (2, 1) - WA (2, 1) = 1 – (-2) = 3).
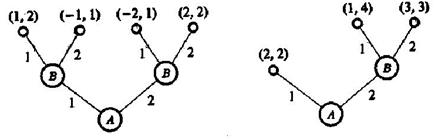
Рис.12 Рис. 13
Пример Б. Игра задается деревом (см. рис. 13).
1-й ход. Игрок А выбирает число х из множества двух чисел {1, 2}.
Если х = 1, то каждый из игроков получает свой выигрыш, равный 2.
Если х = 2, то право 2-го хода получает игрок В, где он и выбирает число у из множества двух чисел {1, 2}.
При у = 1 выигрыш игрока А равен 1, а игрока В — 4. При у = 2 оба игрока получают поровну — по 3.
В случае, когда каждый из игроков стремится к получению максимального выигрыша и любые виды кооперации запрещены, исход игры ясен — игрок А выбирает х = 1, и игра заканчивается. Но при х =2 и у = 2 каждый из игроков получает по 3 (такой исход предпочтительнее простейшего (1, 1)), и, если допустить соглашение между игроками, это обстоятельство вполне может изменить исход игры.
Принятие решений и теория игр. Примеры.
В теории игр рассматриваются ситуации, связанные с принятием решений, в которых два разумных противника имеют конфликтующие цели. К числу типичных примеров относится рекламирование конкурирующих товаров и планирование военных стратегий противоборствующих армий. Эти ситуации принятия решений отличаются от рассмотренных ранее, где природа не рассматривается в роли недоброжелателя.
В игровом конфликте участвуют два противника, именуемые игроками, каждый из которых имеет некоторое множество (конечное или бесконечное) возможных выборов, которые называются стратегиями. С каждой парой стратегий связан платеж, который один из игроков выплачивает другому. Такие игры известны как игры двух лиц с нулевой суммой, так как выигрыш одного игрока равен проигрышу другого. В такой игре достаточно задать результаты в виде платежей для одного из игроков. При обозначении игроков через А и В с числом стратегий m и n соответственно, игру обычно представляют в виде матрицы платежей игроку А:
| B1 | B2 | … | Bn | |
| A1 | a11 | a12 | … | a1n |
| A2 | a21 | a22 | … | a2n |
| . . . | . . . | . . . | . . . | . . . |
| Am | am1 | am2 | … | amn |
Такое представление матричной игры означает, что если игрок А использует стратегию i, а игрок В — стратегию j, то платеж игроку А составляет аij и, следовательно, игроку В — – аij.
Дата: 2016-10-02, просмотров: 343.