Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Часть I МАТРИЧНЫЕ ИГРЫ

Рассмотрим игру, в которой участвуют два игрока, причем каждый из игроков имеет конечное число стратегий. Обозначим для удобства одного из игроков через А, в другого — через В.

Предположим, что игрок А имеет m стратегий — А₁, А₂, ..., А_m, а игрок В имеет n стратегий В₁, В₂, ..., В_n.

Пусть игрок А выбрал стратегию A_i, а игрок В стратегию В_k. Будем считать, что выбор игроками стратегий A_i и В_k однозначно определяет исход игры — выигрыш а_ik игрока А и выигрыш b_ik игрока В, причем эти выигрыши связаны равенством

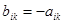
(отрицательный выигрыш на бытовом языке обычно называют проигрышем).

Последнее условие показывает, что в рассматриваемых обстоятельствах выигрыш одного из игроков равен выигрышу другого, взятому с противоположным знаком. Поэтому при анализе такой игры можно рассматривать выигрыши только одного из игроков. Пусть это будут, например, выигрыши игрока А.

Если нам известны значения а_ik выигрыша при каждой паре стратегий (в каждой ситуации) { A_i, В_k }, i = 1, 2,..., m, k = 1, 2,..., n, то их удобно записывать или в виде прямоугольной таблицы, строки которой соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В:

	В1	В1	…	Вn
А1	a11	a11		a11
А2	a11	a11		a11
Аm	am1	a11		amn

 

или в виде матрицы

Полученная матрица имеет размер m x n и называется матрицей игры, или платежной матрицей (отсюда и название игры — матричная).

Рассматриваемую игру часто называют игрой m x n или m x n игрой.

Замечание. Матричные игры относятся к разряду так называемых антагонистических игр, то есть игр, в которых интересы игроков прямо противоположны.

Пример 1. Каждый из двух игроков А и В одновременно и независимо друг от друга записывает на листе бумаги любое целое число. Если выписанные числа имеют одинаковую четность, то игрок А получает от игрока В 1 рубль, а если разную, то наоборот – игрок А платит 1 рубль игроку В.

У игрока А две стратегии: А₁ – записать четное число и А₂ – записать нечетное число. У игро­ка В такие же две стратегии: В₁ – записать четное число и В₂ – записать нечетное число. Выбор игроками соответственно стратегий А_i и В_k однозначно определяет исход игры – выигрыш игрока А.

Матрица этой 2x2 игры имеет следующий вид

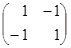
(здесь строки соответствуют стратегиям игрока А, а столбцы — стратегиям игрока В).

 

 

Равновесная ситуация

Рассмотрим следующий пример.

Пример 2. Два игрока А и В, не глядя друг на друга, кладут на стол по картонному кружку красного (г), зеленого (g) или синего (b) цветов, сравнивают цвета кружков и расплачиваются друг с другом так, как покапано в матрице игры

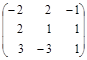
(напомним, что у этой 3 х 3-матрицы строки соответствуют стратегиям игрока А, а столбцы - страте­гиям игрока В).

Считая, что эта 3 х 3 игра повторяется многократно, попробуем определить оптимальные стратегии каждого из игроков.

Начнем с последовательного анализа стратегий игрока А, не забывая о том, что, выбирая страте­гию игрока А, должно принимать в расчет, что его противник В может ответить на нее той из своих стратегий, при которой выигрыш игрока А будет минимальным.

Так, на стратегию А, он ответит стратегией В_r, (минимальный выигрыш равен -2, что на самом деле означает проигрыш игрока А, равный 2), на стратегию А_g – cстратегией B_g или В_b (минимальный выигрыш игрока А равен 1), а на стратегию A_b – стратегией B_g (минимальный выигрыш игрока А равен -3).

Запишем эти минимальные выигрыши в правом столбце таблицы:

	Br	Bg	Bb
Ar	-2		-1	-2
Ag
Ab		-3		-3

maxmin. Неудивительно, что игрок А останавливает свой выбор на стратегии А_g, при которой его минимальный выигрыш максимален (из трех чисел -2, 1 и -3 максимальным является 1):

	Br	Bg	Bb
Ar	-2		-1	-2
Ag
Ab		-3		-3

 

maxmin = 1.

Если игрок А будет придерживаться этой стратегии, то ему гарантирован выигрыш, не меньший 1, при любом поведении противника в игре.

Аналогичные рассуждения можно провести и за игрока В. Так как игрок В заинтересован в том, чтобы обратить выигрыш игрока А в минимум, то ему нужно проанализировать каждую свою стратегию с точки зрения максимального выигрыша игрока А.

Выбирая свою стратегию, игрок В должен учитывать, что при этом стратегией его противника А может оказаться та, при которой выигрыш игрока А будет максимальным. Так, на стратегию В_r он отве­тит стратегией A_b (максимальный выигрыш игрока А равен 3), на стратегию B_g – стратегией A_r (мак­симальный выигрыш игрока А равен 2), а на стратегию B_b – стратегией А_g или A_b (максимальный выигрыш игрока А равен 1). Эти максимальные выигрыши записаны в нижней строке таблицы

	Br	Bg	Bb
Ar	-2		-1	-2
Ag
Ab		-3		-3

minmax. Неудивительно, вели игрок В остановит свой выбор на стратегии B_b, при которой максимальный выигрыш игрока А минимален (из трех чисел 3, 2 и 1 минимальным является 1):

	Br	Bg	Bb
Ar	-2		-1	-2
Ag
Ab		-3		-3

 

minmax = 1.

Если игрок В будет придерживаться этой стратегии, то при любом поведении противника он проиграет не больше 1.

В рассматриваемой игре числа maxmin и minmax совпали:

maxmin = minmax = 1

(соответствующие элементы в таблице

	Br	Bg	Bb
Ar	-2		-1
Ag
Ab		-3

выделены жирным шрифтом).

 

Выделенные стратегии A_g и B_b являются оптимальными стратегиями игроков А и В,

A_g = A_opt, B_b = B_opt

в следующем смысле:

 

Действия игрока А

1-й шаг. В каждой строке матрицы А ищется минимальный элемент

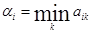, i = 1, 2, … , m.

Полученные числа

α₁, α_{2, …} , α_m

приписываются к заданной таблице в виде правого добавочного столбца

a11	a12	…	a1n	α1
a21	a22	…	a2n	α2
…	…	…	…	…
am1	am2	…	amn	αm

 

Пояснение. Выбирая стратегию А_i, игрок А вправе рассчитывать на то, что в результате разумных действий противника (игрока В) он выиграет не меньше чем а_i.

2-й шаг. Среди чисел

α₁, α_{2, …} , α_m

выбирается максимальное число

или, подробнее,

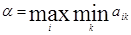
Специально отметим, что выбранное число α является одним из элементов заданной матрицы А.

Пояснение. Действуя наиболее осторожно и рассчитывая на наиболее разумное поведение противника, игрок А должен остановиться на той стратегии A_i, для которой число а_i, является максимальным.

Если игрок А будет придерживаться стратегии, Выбранной описанным выше спосо­бом, то при любом поведении игрока В игроку А гарантирован выигрыш, не меньший α.

Число α называется нижней ценой игры.

Принцип построения стратегии игрока А, основанный на максимизации минимальных выигрышей, называется принципом максимина, а выбираемая в соответствии с этим принципом стратегия А_i⁰ — максиминной стратегией игрока А.

 

Действия игрока В

1 шаг. В каждом столбце матрицы А ищется максимальный элемент

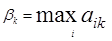, k = 1, 2, … , n.

Полученные числа

β₁, β₂, … , β_n

приписываются к заданной таблице в виде нижней добавочной строки

a11	a12	…	a1n	α1
a11	a22	…	a2n	α2
…	…	…	…	…
a11	am2	…	amn	αm
β1	β2	…	βn

Пояснение. Выбирая стратегию В_k, игрок В должен рассчитывать на то, что в результате разумных действий противника (игрока А) он проиграет не больше чем β_k.

2-й шаг. Среди чисел

β₁, β₂, … , β_n

выбирается минимальное число

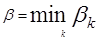
или, подробнее,

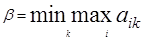
Выбранное число β также является одним из элементов заданной матрицы А.

 

Пояснение. Действуя наиболее осторожно и рассчитывая на наиболее разумное поведение противника, игрок В должен остановиться на той стратегии В_k*, для которой число β_k является минимальным.

 

Если игрок В будет придерживаться стратегии, выбранной описанным выше способом, то при любом поведении игрока А игроку В гарантирован проигрыш, не боль­
ший β.

Число β называется верхней ценой игры.

Принцип построения стратегии игрока B, основанный на минимизации максимальных потерь, называется принципом минимакса, а выбираемая в соответствии с этим принципом стратегия B_k⁰ – минимаксной стратегией игрока В.

Нижняя цена игры α и верхняя цена игры β всегда связаны неравенством

 

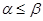
Замечание. Реализация описанного алгоритма требует 2mn - 1 сравнений элементов матрицы А:

(n - 1)m + m - 1 = mn - 1

сравнений для определения α,

(n - 1)m + m - 1 = mn - 1

сравнений для определения β и одно сравнение полученных чисел α и β.

 

Если

,

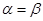или, подробнее,

,

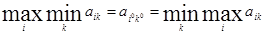то ситуация {А_i⁰, В_k⁰} оказывается равновесной, и ни один из игроков не заинтересован в том, чтобы ее нарушить (в этом нетрудно убедиться путем рассуждений, подобных проведенным при анализе игры в примере 2).

В том случае, когда нижняя цена игры равна верхней цене игры, их общее значение называется просто ценой игры и обозначается через ν.

Цена игры совпадает с элементом 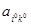матрицы игры А, расположенным на пересечении i⁰-й строки (стратегия 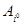игрока А) и k⁰-го столбца (стратегия 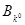игрока В) – минимальный в своей строке и максимальный в своем столбце.

Этот элемент называют седловой точкой матрицы А, или точкой равновесия, а про игру говорят, что она имеет седловую точку.

Стратеги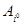и и 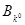, соответствующие седловой точке, называются оптимальными, а совокупность оптимальных ситуаций и цена игры – решением матричной игры с седловой точкой.

 

Замечание. Седловых точек в матричной игре может быть несколько, но все они имеют одно и то же значение.

 

Матричные игры с седловой точкой важны и интересны, однако более типичным является случай, когда применение описанного алгоритма приводит к неравенству

.

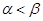Как показывает следующий пример, в этом случае предложенный выбор стратегий уже, вообще говоря, к равновесной ситуации не приводит, и при многократном ее повторении у игроков вполне могут возникнуть мотивы к нарушению рекомендаций, основанных на описанном алгоритме действий игроков А и В.

Пример 3. Рассмотрим 3 x 3 игру, заданную матрицей

.

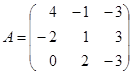Применив предложенный алгоритм

		-3	-3
-2			-2
		-3	-3

 

находим нижнюю цену игры α = -2 и соответствующую ей стратегию А₂, верхнюю цену игры β = 2 и соответствующую ей стратегию B₂.

Нетрудно убедиться в том, что пока игроки придерживаются этих стратегий, средний выигрыш при многократном повторений игры равен 1. Он больше нижней мены игры, но меньше верхней цены.

Однако если игроку В станет известно, что игрок А придерживается стратегии А₂, он немедленно ответит стратегией В₁ и сведет его выигрыш к проигрышу -2. В свою очередь, на стратегию В₁ у игрока А имеется ответная стратегия А₁, дающая ему выигрыш 4.

Тем самым, ситуация { А₂, В₂} равновесной не является.

 

 

Смешанные стратегии

В случае, когда нижняя цена игры α и верхняя цена игры β не совпадают,

,

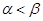игрок А может обеспечить себе выигрыш, не меньший α, а игрок В имеет возможность
не дать ему больше, чем β. Возникает вопрос – а как разделить между игроками разность

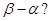
Предыдущие построения на этот вопрос ответа не дают — тесны рамки возможных действий игроков. Поэтому довольно ясно, что механизм, обеспечивающий полу­чение каждым из игроков как можно большей доли этой разности, следует искать в определенном расширении стратегических возможностей, имеющихся у игроков изначально.

Оказывается, что компромиссного распределения разности между игроками и уверенного получения каждым игроком своей доли при многократном повторении игры можно достичь путем случайного применения ими своих первоначальных, чи­стых стратегий. При таких действиях

– во-первых, обеспечивается наибольшая скрытность выбора стратегии (результат выбора не может стать известным противнику, поскольку он неизвестен самомуигроку),

– во-вторых, при разумном построении механизма случайного выбора стратегий, последние оказываются оптимальными.

Случайная величина, значениями которой являются стратегии игрока, называется его смешанной стратегией.

Тем самым, задание смешанной стратегии игрока состоит в указании тех вероятностей, с которыми выбираются его первоначальные стратегии.

 

 

Основные определения

Рассмотрим произвольную m х n игру, заданную m х n-матрицей

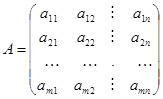
Так как игрок А имеет m чистых стратегий, то его смешанная стратегия может, быть описана набором m неотрицательных чисел

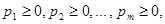
сумма которых равна 1,

.

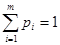Смешанная стратегия второго игрока В, имеющего п чистых стратегий, описыва­ется набором п неотрицательных чисел

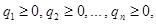
сумма которых равна 1,

.

 

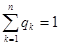Замечание. Каждая чистая стратегия является частным случаем смешанной стратегии: в частности, чистая стратегия A_i является смешанной стратегией, описываемой набором чисел Рев котором p₁, p₂, … , p_m, в котором

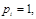
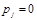
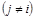
Подчеркнем, что для соблюдения секретности каждый из игроков применяет свои стратегии независимо от другого игрока.

Таким образом, задав два набора

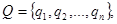
мы оказываемся в ситуации в смешанных стратегиях. В этих условиях каждая обычная ситуация (в чистых стратегиях) {А_i, B_k} по определению является случайным событием и, ввиду независимости наборов Р и Q, реализуется с вероятностью p_iq_k. В этой ситуации {А_i, B_k} игрок А получает выигрыш a_ik. Тем самым, математическое ожидание выигрыша игрока А в условиях ситуации в смешанных стратегиях (Р, Q) равно

.

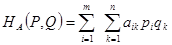Это число и принимается за средний выигрыш игрока А при смешанных стратегиях

 

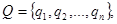
Определение. Стратеги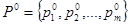и

и

называются оптимальными смешанными стратегиями игроков А и В соответственно, если выполнено следующее соотношение

.

 

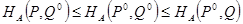Пояснение. Выписанные неравенства означают следующее:

левое неравенство – отклонение игрока А от оптимальной стратегии Р⁰ при условии, что игрок В придерживается стратегии Q⁰, приводит к тому, что выигрыш отклонившегося игрока А может только уменьшиться,

правое неравенство – отклонение игрока В от оптимальной стратегии Q⁰ при условии, что игрок А придерживается стратегии Р⁰, приводит к тому, что выигрыш игрока А может только возрасти, и значит, выигрыш игрока В – только уменьшиться.

 

Приведенное условие оптимальности равносильно тому, что[1]

Величина

,

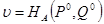определяемая последней формулой, называется ценой игры.

Набор (Р⁰, Q⁰, ν), состоящий из оптимальных смешанных стратегий игроков А и В и цены игры, называется решением матричной игры.

 

Пример 4. Рассмотрим 2 x 2 матричную игру из примера 1. Матрица этой игры имеет следующий вид

.

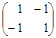Как нетрудно убедиться, седловой точки у нее нет.

Смешанные стратегии игроков А и В могут быть описаны парами чисел

P = {p, 1 - p} и Q = {q, 1 - q}

соответственно.

Средний выигрыш игрока А вычисляется так

?

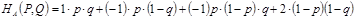откуда легко следует, что

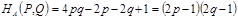
Последнее удобно записать так

.

 

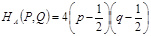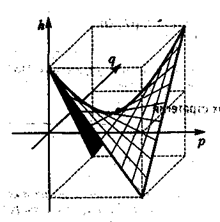
Рис. 1

Полученная формула показывает, что если игрок А в половине случаев записывает на листе бумаге четное (нечетное) число (выбирает р = 1/2), то независимо от того, что делает игрок В, ожидаемый (средний) вы­игрыш игрока А в каждой партии будет нулевым.

Если же игрок А выберет р > 1/2 (так что разность р-1/2 будет положительной), то узнав об этом, игрок В может выбрать q < 1/2 (так что разность q - 1/2 будет отрицательной) и, тем самым, сделать средний выигрыш игрока А отрицательным, то есть заставит его проиграть. Если же игрок А выберет р < 1/2 (так что разность р -1/2 будет отрицательной) и игрок В узнает об этом, то он может выбрать q > 1/2 (так что разность q -1/2 бу­дет положительной) и вновь сделать выигрыш игрока А отрицательным, то есть опять заставит его проиграть.

Исследуем теперь эту формулу с точки зрения игро­ка В.

Если игрок А выбирает р = 1/2, то ожидаемый (средний) выигрыш игрока B независимо от его дей­ствий будет нулевым в каждой партии. Но если игрок В выберет q > 1/2 (так что разность q - 1/2 будет положительной), то, узнав об этом, игрок А может выбрать р < 1/2 (так что разность р - 1/2 будет отри­цательной), и тогда игрок В будет проигрывать в каждой партии. Если же игрок В выберет q < 1/2 (так что разность q -1/2 будет отрицательной) и игрок А узнает об этом, то он может выбрать р > 1/2 (так что разность р -1/2 будет положительной) и вновь заставит игрока В проиграть.

Тем самым наборы

,

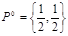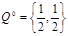
является оптимальными, а исход игры ничейным:

ν = 0.

Замечание. На рисунке 1 показано, как устроена поверхность, описываемая функцией

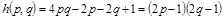
Точка

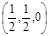
является седловой точкой (точкой перевала) этой поверхности. Именно эта точка и дает решение рассматриваемой матричной игры.

 

Естественно возникают два ключевых вопроса:

1-й – какие матричные игры имеют решение в смешанных стратегиях?

2-й – как находить решение матричной игры, если оно существует?

Ответы на эти вопросы дают следующие две теоремы.

 

X n игры

Пусть

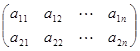
- платежная матрица 2 х n игры.

Согласно теореме о двойном описании игры (теорема 2) нахождение цены игры и оптимального значения р⁰ для игрока А равносильно разрешению уравнения

.

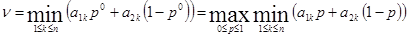Опишем общую схему, приводящую к искомому результату.

Максимум функции

(*)

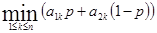проще всего найти, построив ее график. Для этого поступают следующим образом.

Предположим, что игрок А выбрал смешанную стратегию Р = {р, 1 - р}, а игрок В - k-ю чистую стратегию, k = 1, 2, ... , n. Тогда средний выигрыш игрока А в ситуации {Р, k} оказывается равным

(k): .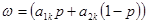

На плоскости (р, ω) уравнение (k) описывает прямую. Тем самым, каждой чистой стратегия игрока B на этой плоскости соответствует своя прямая.

Поэтому сначала на плоскости (ω, р) последовательно и аккуратно рисуются все
прямые

(k): 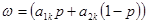, k = 1, 2, ... , n

(рис.2). Затем для каждого значения р, 0 £ р £ 1, путем визуального сравнения соответствующих ему значений ω на каждой из построенных прямых определяет­ся и отмечается минимальное из них (рис. 3). В результате описанной процедуры получается ломаная, которая и является графиком функции (*) (выделена жирным на рис. 4). Эта ломаная как бы огибает снизу все семейство построенных прямых,

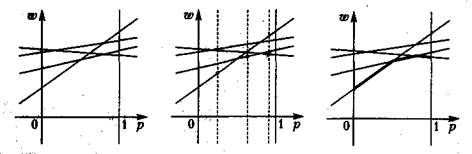
Рис.2 Рис.3 Рис.4

 

и по этой причине ее принято называть нижней огибающей этого семейства. Верхняя точка построенной нижней огибающей определяет и цену игры – v и оптимальную стратегию игрока А – Р⁰ = {р⁰, 1 - р⁰} (рис. 5).

 

Замечание. Описанная процедура может рассматриваться как некоторый аналог максиминного подхода при отсутствии седловой точки.

 

Опробуем описанную схему решения 2 х n игры на конкретном примере.

 

Пример 5. Рассмотрим игру, заданную 2 x 6 матрицей

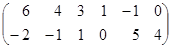
Решение.

1-й шаг. Анализ игры на наличие седловой точки.

Нижняя цена игры равна -1, верхняя цена игры равна 1. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.

2-й шаг. Вычисление средних выигрышей игрока А (проводится при условии, что игрок В выбирает только чистые стратегии).

Из таблицы

p					-1
1 - p	-2	-1

 

легко получаем:

(1): ω = 6p - 2(1 - p),

(2): ω = 4p - (1 - p),

(3): ω = 3p + (1 - p),

(4): ω = p ,

(5): ω = 6p - 2(1 - p),

(6): ω = 4(1 - p),

3-й шаг. Построение нижней огибающей.

Аккуратно строим на координатной плоскости (р, ω) все шесть прямых, уравнения которых полу­чены на 2-м шаге (рис. 6), и находим их нижнюю огибающую.

4-й шаг. Отыскание цены игры и оптимальной смешанной стратегии игрока А.

При аккуратном построении нижней огибающей, нетрудно определить, точкой пересечения каких двух из построенных шести прямых является ее наивысшая точка. В данном случае это прямые (4) и (5), заданные уравнениями ω = р и ω = -р + 5(1 - р) соответственно. Решая систему уравнений

ω = р,

ω = -p + 5(l - p), ,

получаем

,

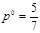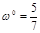
(рис.7).

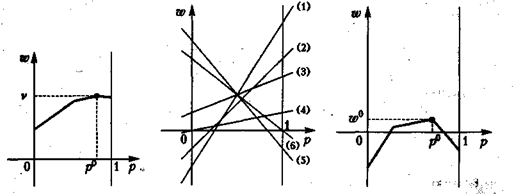
Рис.5 Рис.6 Рис.7

 

Тем самым, цена игры ν и оптимальная стратегия Р⁰ игрока A соответственно равны

, .

 

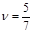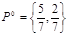Собственно, этим и заканчивается решение игры для игрока А, поскольку его в первую очередь интересует отыскание собственной оптимальной стратегии и ожидаемого наилучшего гарантированного результата.

 

Замечание. Решающий матричную игру обычно отождествляет себя с одним из игроков (как правило, это игрок А), считая другого своим противником. Это связано еще и с тем, что в некоторых случаях основное внимание уделяется поиску оптимальных стратегий только игрока А, а стратегии противника могут вообще не интересовать исследователя.

 

Однако в целом ряде случаев оказывается важным знать оптимальные смешанные стратегии обоих игроков.

Как ищется оптимальная смешанная стратегия игрока А, мы уже описали. Покажем теперь, как отыскать оптимальную смешанную стратегию игрока В.

Здесь, в зависимости от формы нижней огибающей, может представиться несколь­ко случаев.

А. Нижняя огибающая имеет ровно одну наивысшую точку (р⁰, ω⁰):

1) Если р⁰ = 0 (оптимальная стратегия игрока А – чистая стратегия А₂), то игро­ку В выгодно применять чистую стратегию, соответствующую номеру прямой, проходящей через точку (0, ω⁰) и имеющей наибольший отрицательный наклон (рис. 8).

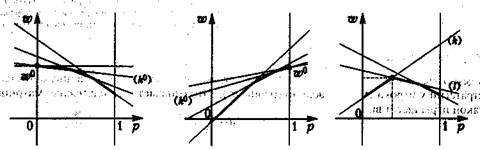
Рис.8 Рис.9 Рис.10

 

2) Если p⁰ == 1 (оптимальная стратегия игрока А — чистая стратегия А₁), то опти­мальной для игрока В является чистая стратегия, соответствующая номеру прямой, проходящей через точку (1, ω⁰) и имеющей наименьший положительный наклон (рис. 9).

3) Если 0 < p⁰ < 1, то в наивысшей точке нижней оги­бающей пересекаются, по меньшей мере, две прямые, одна из которых (k-я) имеет положительный наклон, а другая (l-я) — отрицательный (рис. 10), и оптимальная смешан­ная стратегия игрока В получается, если положить

q_k = q, q_l = 1 - q, q_j = 0, j ≠ k, l.

где q – решение уравнения

.

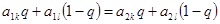Б. Нижняя огибающая содержит горизонтальный участок, соответствующий чистой стратегии k⁰ игрока B, которая и является оптимальной для него (рис. 11).

Рис. 11

 

Пример 5 (продолжение). Покажем теперь, как найти полное решение игры, то есть еще и оптимальную смешанную стратегию

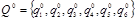
игрока В.

Для этого поступают так:

1) полагают

(выделяя тем самым из шести чистых стратегий игрока В стратегии В₄ и B₅. которым соответствуют прямые (4) и (5), определяющие наивысшую точку нижней огибающей),

 

2) приравнивают любой из двух средних выигрышей игрока В (игрок А выбирает только чистые стратегии), отвечающих предложенной смешанной стратегии

			q	1 - q
				-1
-2	-1

к цене игры

,

 

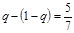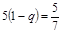
3) получают (в обоих случаях), что

.

Полное решение игры имеет следующий вид

, , .

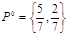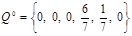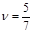Замечание. Ситуация с наличием лишь двух конкурирующих стратегий игрока А нельзя считать на­думанной. Она возникает сравнительно часто. Например, в случае, если нужно сравнить два образца некоторого изделия (скажем, старого и модернизированного) с целью выяснения возможности замены, это весьма удобно сделать при помощи платежной матрицы 2 х n.

 

M х 2 игры

Пусть теперь в матричной игре две чистые стратегии имеет игрок В, а число чистых стратегий у игрока А произвольно (равно m). Это означает, что платежная матрица такой игры имеет вид

.

Анализ такой игры во многом напоминает рассуждения, описанные для игры 2 х n.

Пусть Q = {q, 1 - q} — произвольная смешанная стратегия игрока В. Если игрок А выбирает i-ю чистую стратегию, i = 1, 2, ... , n, то средний выигрыш игрока В в ситуации {i, Q} будет равным

 

(i): 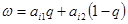i = 1, 2,..., m. (*)

Зависимость этого выигрыша от переменной q описывается прямой.

Графиком функции

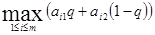
является верхняя огибающая семейства прямых (*), соот­ветствующих чистым стратегиям игрока А (рис. 12).

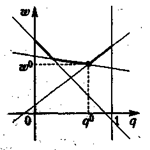
Рис.12

 

Абсциссой нижней точки полученной ломаной будет значение q⁰, определяющее оптимальную смешанную стра­тегию игрока В, а ординатой ω⁰ – цена игры.

Замечание. Отыскание оптимальной смешанной стратегии игрока А проводится по той же схеме, которая позволяет находить оптимальную смешанную стратегию игрока В в игре 2 х n.

Рассмотрим конкретный пример.

Пример 6. 3 х 2 игра задана матрицей

.

 

Решение.

1 шаг. Анализ игры на наличие седловой точки.

Нижняя цена игры равна 0, верхняя цена игры равна 3. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях.

2-й шаг. Вычисление средних выигрышей игрока В (проводится при условии, что игрок А выбирает только чистые стратегии).

Из таблицы

q	1 - q
	-1
-1

 

получаем:

(1): ω = 3q – (1 - q)

(2): ω = -q + 3(1 - q)

(3): ω = q

3-й шаг. Построение верхней огибающей.

Построим на координатной плоскости (q, ω) все три прямых, а за­тем и их верхнюю огибающую (рис. 13).

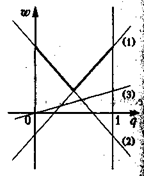
Рис. 13

4-й шаг. Отыскание иены игры и оптимальной смешанной стратегии игрока В.

Нижняя точка верхней огибающей является точкой пересечения прямых (1) и (2). Решая систему уравнений

ω = 3q – (1 - q),

ω = -q + 3(1 - q),

получаем

, .

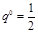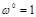5-й шаг. Отыскание оптимальной смешанной стратегии игрока А.

Полагая

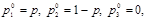
приравниваем средние выигрыши игрока А, соответствующие чистым выигрышам игрока В,

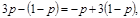
и находим р⁰ = 1/2.

Таким образом, цена игры и оптимальные смешанные стратегии игроков А и В соответственно

.

 

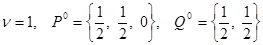M х n игры

В принципе решение любой матричной юры сводится к решению стандартной задачи линейного программирования и, тем самым, может быть найдено методами линейного программирования. При этом требуемый объем вычислений напрямую зависит от числа чистых стратегий игроков (растет с его увеличением и, значит, с увеличением размеров матрицы игры). Поэтому любые приемы предварительного анализа игры, позволяющие уменьшать размеры ее платежной матрицы или еще как-то упрощать эту матрицу, не нанося ущерба решению, играют на практике весьма важную роль

 

Правило доминирования

В целом ряде случаев анализ платежной матрицы обнаруживает, что некоторые чистые стратегам не могут внести никакого вклада в искомые оптимальные смешанные стратегии. Отбрасывание подобных стратегий позволяет заменить первоначальную
матрицу на матрицу выигрышей меньших размеров.

Опишем одну из таких возможностей более подробно.

— произвольная m х n-матрица. Бу