А. Автокорреляция сигналов
3.1. АКФ прямоугольного видеоимпульса.Установите заданные значения E, tИ (прил. П4.3), введите t = 0. При этом ПЭВМ вычислит и отметит точками три значения АКФ: в точке t = 0 и в двух соседних точках t = ± 0.07 мс.
Примечание. Здесь и далее ПЭВМ вычисляет сначала спектральную плотность и энергетический спектр, затем по энергетическому спектру корреляционную функцию. При исследовании механизма получения АКФ и ВКФ корреляционные функции вычисляются повторно, непосредственно по временным функциям.
С помощью метки F6 по АКФ определите энергию видеоимпульса, а также значения спектров S(0), W(0). Сравните результаты измерений с расчетными значениями, полученными в домашней работе. Выведите на принтер содержимое экрана.
Изменяя значения t в пределах ± tи, ознакомьтесь и изучите механизм получения АКФ. Зафиксируйте величину интервала корреляции tк для данного сигнала.
Далее, при t = 0 выполните вариации tи и исследуйте взаимосвязь ширины спектров S(w), W(w) и интервала корреляции АКФ. Зафиксируйте несколько ситуаций (в виде таблицы), используйте полученные результаты при составлении отчета.
3.2.АКФ прямоугольного радиоимпульса. Изучите механизм получения АКФ радиоимпульса с заданными параметрами T, tИ, f0 (прил. П4.3) путем перебора значений t. Используя “линзу”, рассмотрите подробнее:
- заданный радиоимпульс и измерьте период несущего колебания;
- полученную АКФ ромбовидной формы; здесь также измерьте частоту (период) несущего колебания и обратите внимание на максимальную точку В(0), измерьте также В(ti) для ti = 0.07 мc или ti = - 0.07 мс;
- подынтегральное произведение, где сомножителями являются радиоимпульс и его копия при любом сдвиге t (кроме t = 0).
Максимально “раздвиньте” все три произведения (F5) с тем, чтобы разместилось не более 2...3-х периодов несущего колебания и распечатайте полученную информацию (содержимое экрана). При составлении отчета вычислите значения В(0) и В(ti) для данного ti :
- по площади, соответствующей произведению сигнала и его копии;
- аналитически, выставив заданные параметры сигнала и смещение ti.
3.3. АКФ треугольного и пилообразного импульсов. Ознакомьтесь с механизмом получения АКФ этих импульсов без каких - либо измерений и без получения распечаток. В отчете отметьте вид получаемых АКФ.
3.4.АКФ видеосигналов Баркера. Изучите АКФ и спектры видеосигналов Баркера с заданными параметрами E, tИ, q (см. прил. П4.2 и П4.3). Изменяя t, проследите за изменениями трёх соответствующих значений АКФ, выделенных цветными точками на графике АКФ. визуально оцените соответствие этих значений результирующим площадям в трёх окнах дисплея, образованным подынтегральными произведениями сигнала и его смещенной копии. Выведите на принтер ситуацию для любого t.
Измерьте значения S(w) в двух точках: при w = 0 и на частоте выброса (или провала) спектральной плотности. При составлении отчета эти же значения необходимо вычислить по спектральной функции, приведённой в прил. П4.2.
3.5.АКФ ЛЧМ сигнала. Ознакомьтесь с механизмом формирования АКФ сигнала с линейной частотной модуляцией с параметрами: f0 - центральная частота, fд - девиация частоты, Е - амплитуда, tИ - длительность импульса (см. прил. П4.3). Обратите внимание на лепестковый характер и ярко выраженный максимум АКФ.
Б. Взаимная корреляция сигналов
3.6. Ознакомьтесь с ВКФ для следующих комбинаций сигналов.
Таблица 4.1
Комбинация видеосигналов
| 1-й видеоимпульс | 2-й видеоимпульс |
| прямоугольный | треугольный |
| прямоугольный | пилообразный |
| треугольный | пилообразный |
Убедитесь, что при t = 0 ВКФ вовсе не обязательно достигают максимума и что ВКФ необязательно четная функция (как АКФ). Наблюдения отразите в отчете, приведите примеры.
3.7. Проверьте экспериментально, не будет ли разницы между корреляционными функциями
 и
и 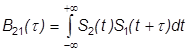 .
.
Для этого в режиме ВКФ сначала в качестве первого сигнала выберите прямоугольный импульс, а в качестве второго - пилообразный (параметры сигналов заданы в прил. П4.3). получите В12(t), измерьте значения В12(t) в трёх точках: t = 0, t = ±0,07 мс. Распечатайте содержимое экрана при t = 0.
Затем поменяйте местами сигналы: в качестве первого задайте пилообразный импульс, а второго - прямоугольный (с теми же параметрами). измерьте значения В21(t)
в тех же трёх точках t. содержимое экрана с функцией В21(t) такжераспечатайте.
При составлении отчета выскажитесь по поводу В12(t) и В21(t), приведите их аналитические выражения из приложения П4.1. Ответьте также на вопросы:
- справедливо ли здесь равенство В21(t) = В12(-t)?
- будет ли разница между В21(t) и В12(t) в случае разных, но симметричных относительно оси ординат сигналов S1(t) и S2(t)?
При составлении отчета выполните поверочные расчеты: вычислите по одному значению В12(t) и В21(t), измеренные в этом пункте работы, причем t можно взять любым, но одинаковым для обеих ситуаций.
В. Автокорреляция дискретных сигналов
3.8. При наборе кода в режиме АКФ необходимо, чтобы код 1-го сигнала совпадал с кодом 2-го. Для исследования можно задать любой дискретный сигнал, но интереснее (и полезнее) работать с кодами Баркера. Введите заданную амплитуду Е (прил. П4.3). Ознакомьтесь с механизмом получения дискретной АКФ (точнее ДАКФ) по ромбовидной матрице. Изменяя величину сдвига второго сигнала изменением n, установите любую наиболее наглядную ситуацию, при которой В(n) ¹ 0. выведите результаты на принтер.
При составлении отчета проверьте правильность полученного результата, вычислив В(n) по формуле дискретной корреляционной функции.
Г. Взаимная корреляция дискретных сигналов
3.9. Сформируйте дискретную модель радиоимпульсов (+ - + - + - + - + - + -), причем одинаковую для обоих сигналов, и получите ДАКФ. Изучите механизм получения корреляционной функции по ромбовидной матрице и при любом значении дискретного сдвига (n ¹ 0). распечатайте содержимое экрана.
Повторите эксперимент, изменив второй радиоимпульс по фазе на 180°, т. е. наберите следующий код второго сигнала: (- + - + - + - + - + - +). Зафиксируйте изменения в ДВКФ и прокомментируйте их в отчете.
4. Контрольные вопросы
А. Вопросы для коллоквиума
4.1. Запишите аналитическое определение АКФ и ВКФ.
4.2. Назовите свойства АКФ и ВКФ.
4.3. Влияет ли начальная фаза сигнала на корреляционную функцию?
4.4. Что такое энергетический спектр сигнала и как он связан с его спектральной плотностью?
4.5. Дайте определение взаимного энергетического спектра двух сигналов и укажите его физический смысл.
4.6. Каким должен быть взаимный энергетический спектр двух ортогональных сигналов? Почему?
4.7. Как связаны АКФ и энергетический спектр сигнала? Укажите аналитическую связь между ВКФ и взаимным энергетическим спектром двух сигналов.
4.8. Какая разница между корреляционными функциями периодических и непериодических сигналов.
Б. Вопросы на защите отчета
4.9. Как влияет ширина спектра сигнала на интервал корреляции АКФ? Приведите пример из лабораторной работы.
4.10. Сформулируйте и запишите равенство Парсеваля для непериодического сигнала. Приведите иллюстрацию этого соотношения из выполненной работы.
4.11. На какой частоте имеет место провал (или выброс) в первом лепестке спектральной плотности видеосигнала Баркера? В каких случаях наблюдается такой провал, а в каких выброс?
4.12. Объясните разницу в ВКФ B12(t) и B21 (t) прямоугольного и пилообразного импульсов в п. 3.6 лабораторной работы.
4.13. Чем определяется максимум АКФ? Приведите иллюстрацию из работы.
4.14. Зависит ли величина максимума АКФ сигнала Баркера от базы сигнала?
4.15. Объясните механизм сжатия и накопления сигнала при получении АКФ (на примерах ЛЧМ - сигнала и видеосигнала Баркера).
4.16. Укажите особенности корреляционного анализа дискретных сигналов.
ПРИЛОЖЕНИЯ
Приложение П4.1
Дата: 2016-10-02, просмотров: 601.