Расшифруем слагаемые уравнения теплового баланса печи, работающей в неизотермическом режиме реактора идеального перемешивания.

При составлении балансовых уравнений в качестве элементарного объема берут элементарный объем топки, работающий п режиме полного перемешивания.

Тогда тепловые потоки за момент времени 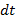для объема топки составят:

(5.7)

где 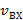- объемная скорость топливно-воздушной смеси на входе в топку, м³/ч;

- средняя теплоемкость топливно-воздушной смеси на входе в топку, Дж/кг·град;

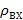- средняя плотность топливно-воздушной смеси на входе в топку, кг/м³;

- средняя температура топливно-воздушной смеси на входе в топку, °С.

(5.8)

где - объемная скорость топливно-воздушной смеси на выходе из топки, м³/ч;

- средняя теплоемкость топливно-воздушной смеси на выходе из топки, Дж/кг·град;

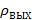- средняя плотность топливно-воздушной смеси на выходе из топки, кг/м³;

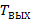- средняя температура топливно-воздушной смеси на выходе из топки, °С.

(5.9)

где - энтальпия реакции горения 1 м³ топлива, кДж/м³;

- объем топки, м³;

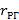- скорость реакции горения, ч^-1 (м³/м³ ч).

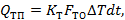
(5.10)

где - коэффициент теплопередачи, Дж/м²·С;

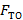- поверхность теплообмена, м²;

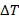- средняя разность температур в топке и внешней среды, °С.

(5.11)

где - теплота фазового перехода топлива и/или продуктов сгорания, кДж;

- энтальпия фазового перехода топлива и/или продуктов сгорания, кДж/ч.

(5.12)

Итак, уравнение теплового баланса топки для нестационарного режима примет вид:

(5.13)

В стационарном режиме правая часть уравнения (5.13) равна нулю. Если принять, что и и , то для стационарного режима можно записать:

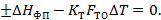
(5.14)

Для последующего анализа уравнения (5.14) его удобнее записать в следующем виде:

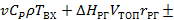
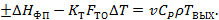
(5.15)

Из уравнения (5.15) видно, что эффективность сжигания топлива в топке определяется энтальпией реакции горения топлива . Чем энтальпия выше, т.е. чем полнее протекает реакция горения топлива, и чем оно калорийнее, тем больше тепла выделяется при сжигании единицы топлива и тем выше температура выходящих продуктов сгорания .

Эффективность сжигания топлива в печи уменьшается с ростом тепловых потерь через стенку .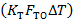

В случае использования жидкого топлива эффективность снижается вследствие затрат тепла на испарение мазута, а повышается в случае конденсации водяного пара из продуктов сгорания. Поэтому знак (+) или (-) в уравнении определяется балансом, например, - если тепло, выделившееся при конденсации водяного пара, превысит тепло, затраченное на испарение мазута, и - если наоборот.

Аналогично рис. 5.1 выглядят поточная диаграмма Сенке материального баланса по воде для теплоэлектростанции (ТЭС), приведенная на рис. 5.2

В уравнении материального баланса (по воде) учитываются все потоки воды на входе в ТЭС и на выходе из нее. В приведенной на рис. 5.2 схеме для охлаждения воды ТЭС используют градирню (Г). Для стационарного режима работы ТЭС накопление воды в ТЭС равно 0.

Из представленной на рис. 5.2 диаграммы в силу закона сохранения массы вещества можно записать:

(5.16)

В ТЭС поступает холодный водяной поток 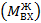, состоящий из «свежей» воды речного водозабора и циркулирующей воды , охлажденной в градирне (Г).

Если пренебречь потерями воды в ТЭС при производстве тепловой и электрической энергии, то количество выходящей горячей воды равно:

(5.17)

Рис. 5.2. Поточная диаграмма Сенке для материального баланса ТЭС по воде

Охлаждение воды ТЭС в градирне перед ее частичным сбросом в водоем происходит за счет частичного испарения воды . Тогда уравнение для примет вид:

(5.18)

Из уравнений 5.17 и 5.18 можно вычислить количество воды , теряющейся за счет испарения в градирне:

(5.19)

Потеря воды компенсируется водозабором из реки.

Эксергия

Для анализа эффективности различных энерготехнологических схем превращения энергии и тепловых процессов часто используют понятие эксергии. Эксергия - это энергия, пригодная для использования. В процессах преобразования энергии она характеризует ее работоспособность. Совершенство аппаратов (печей, парогенераторов, паросиловых установок и др.), производящих тепло, оценивают эксергетическим КПД. Эксергию определяют через максимальную работу, которая может быть получена при обратимом переходе рассматриваемой системы в равновесное состояние с окружающей средой. Использование эксергии для термодинамического анализа называется эксергетическим методом.

Реально протекающие процессы необратимы. При совершении процесса качество эксергии понижается. Например, отработанный пар характеризуется более низкими значениями температуры и давления и вследствие этого может совершить меньше работы. Следить за потоками эксергии удобно с помощью эксергетических диаграмм Сенке.

Детальное рассмотрение эксергии и ее приложений для термодинамического анализа различных систем выходит за рамки курса «Основы ресурсо-энергосберегающих технологий углеводородного сырья».

Более подробные сведения об эксергии содержатся в специальной литературе по технической термодинамике и теплотехнике.