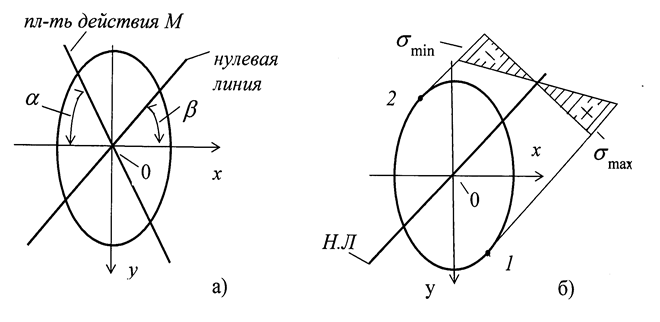
Рис. 2.7
Сначала надо определить положение нейтральной (нулевой) линии. Во всех точках этой линии поперечного сечения нормальные напряжения равны нулю, т.е. 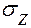 = 0.
= 0.
Угол наклона 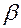 нулевой линии (рис .2.7,а) определяется из формулы:
нулевой линии (рис .2.7,а) определяется из формулы: 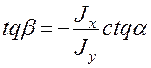 = k.
= k.
Уравнение нейтральной линии имеет вид y = kx. Она проходит через центр тяжести сечения и в общем случае не перпендикуляр-на к плоскости изгибающего момента, а несколько повернута в сто-рону оси минимального момента инерции. Нулевая линия будет перпендикулярна плоскости изгибающего момента, если 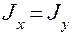 (круглое сечение, квадратное и др.).Зная положение нулевой линии, можно найти в сечении опасные точки 1 и 2. Эти точки наиболее удалены от нулевой линии. Определив из чертежа (рис. 2.7,б) координаты этих точек: т. 1(
(круглое сечение, квадратное и др.).Зная положение нулевой линии, можно найти в сечении опасные точки 1 и 2. Эти точки наиболее удалены от нулевой линии. Определив из чертежа (рис. 2.7,б) координаты этих точек: т. 1( 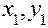 ), т. 2 (
), т. 2 ( 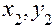 ), рассчитаем напряжения
), рассчитаем напряжения 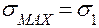 и
и 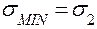 :
:
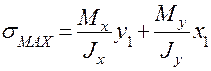 ;
; 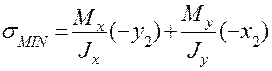 .
.
Пример. Для консольной балки, изображенной на рис. 2.8 , по- 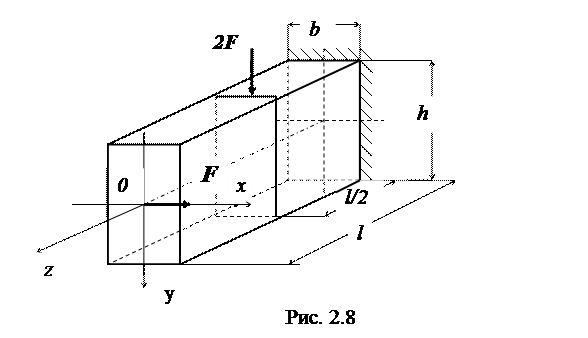
добрать размеры прямоугольного поперечного сечения (h = 2b). Дано: F = 1 кН, l = 1 м, [ 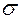 ]=160 МПа.
]=160 МПа.
Решение
Приложенные силы перпендикулярны к оси z и вызывают поперечные изгибы балки в вертикальной и горизонтальной плоскостях. Эпюры изгибающих моментов показаны на рис. 2.9,а.
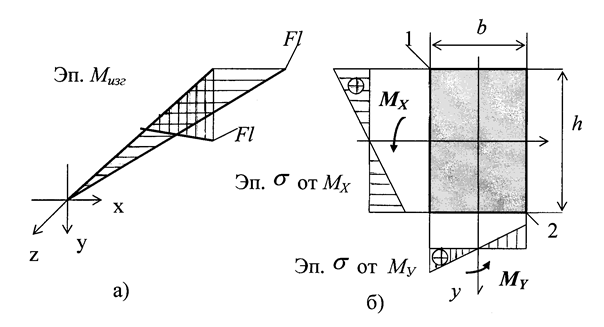
Рис. 2.9
Изгибающие моменты в плоскости действия сил изменяются по линейному закону и наибольших значений достигают в заделке. Покажем это поперечное сечение балки и эпюры распределения нормальных напряжений от МХ и МУ (рис. 2.9,г). Из эпюр напряжений следует, что опасными точками сечения являются точки 1 и 2 .
Условие прочности для опасной точки 1 имеет вид:
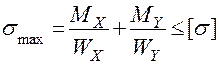 ,
,
где MX = MY = Fl.
Учтя, что WX = bh2/6 = b3·2/3; WY = hb2/6 = b3/3,
получим 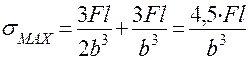 .
.
Приравнивая полученное выражение для максимального напряжения допускаемому, находим значение размера b:
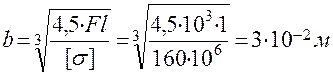 . Тогда h = 6·10-2 м.
. Тогда h = 6·10-2 м.
Определение напряжений в произвольной точке сечения при внецентренном растяжении бруса
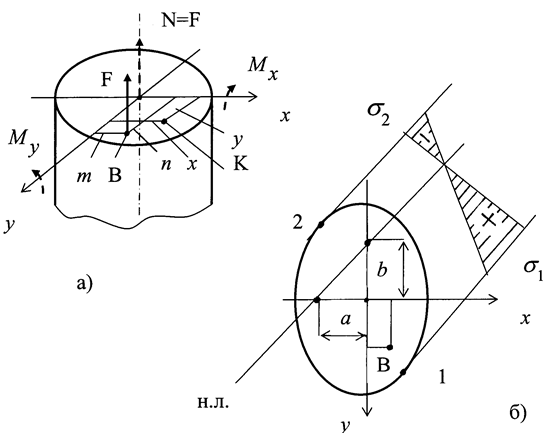
Рис. 2.10
В любом поперечном сечении бруса возникают нормальная сила N и изгибающие моменты 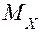 ,
, 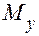 (рис. 2.10,а) :
(рис. 2.10,а) :
N = F ; 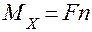 ;
; 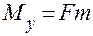 .
.
Здесь n, m - координаты точки В, в которой приложена сила F. Напряжения в произвольной точке К сеченияс координатами х,у определяются по формуле:
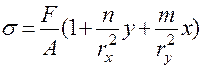 . Здесь А площадь сечения. Величины
. Здесь А площадь сечения. Величины 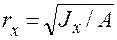 ;
; 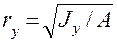 характеризуют геометрию сечения и называются радиусами инерции сечения относительно осей х и у.
характеризуют геометрию сечения и называются радиусами инерции сечения относительно осей х и у.
Определение опасных точек в поперечном сечении бруса при внецентренном растяжении - сжатии
Для определения точек с наибольшими напряжениями в поперечном сечении произвольной формы вначале необходимо установить положение нулевой линии.
Уравнение нулевой линии можно представить в виде уравнения прямой в отрезках:
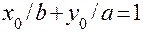 ,
,
где 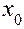 и
и 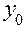 - координаты текущей точки нулевой линии.
- координаты текущей точки нулевой линии.
Отрезки, отсекаемые нулевой линией на осях координат равны: 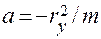 ,
, 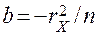 .
.
Определив положение нулевой линии, строят эпюру нормальных напряжений (рис. 2.10,б).
Напряжения 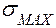 и
и 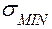 возникают в наиболее удаленных от нулевой линии точках 1 (
возникают в наиболее удаленных от нулевой линии точках 1 ( 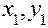 ) и 2 (
) и 2 ( 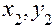 ), которые находятся путем проведения касательной прямой к сечению параллельно нулевой линии.
), которые находятся путем проведения касательной прямой к сечению параллельно нулевой линии.
Ядро сечения
Ядром сечения называется область в окрестности центра тяжести сечения, обладающая следующим свойством. Если приложить силу F внутри или на границе ядра сечения, то во всем сечении напряжения будут одного знака.
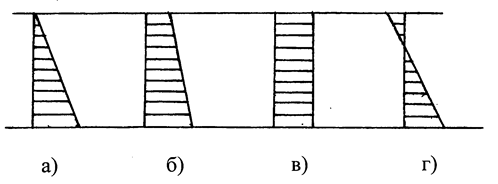
Рис. 2.11
На рис. 2.11 показаны эпюры нормальных напряжений в сечении бруса, если сила приложена а) - на контуре ядра сечения, б) - внутри, г) вне ядра сечения и в) - в центре тяжести сечения бруса.
Тема 3. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ СЛОЖНОМ НАПЯЖЕННОМ СОСТОЯНИИ
ЗАДАЧА 3.1.
Элемент, показанный на рис. 3.1,а, находится под действием напряжений  ,
, 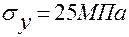 ,
, 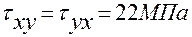 . Требуется найти величину главных напряжений и положение площадок, по которым они действуют.
. Требуется найти величину главных напряжений и положение площадок, по которым они действуют.
Решение.
Для рассматриваемого элемента одна из главных площадок (плоскость хоу) известна. Требуется определить положение двух других главных площадок и значения главных нормальных напряжений, действующих на этих площадках. При подстановке значений напряжений в формулы нам потребуются следующие правила знаков. Растягивающее нормальное напряжение 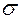 считается положительным, сжимающее – отрицательным. Касательное напряжение
считается положительным, сжимающее – отрицательным. Касательное напряжение 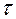 положительно, если оно стремится повернуть элемент по часовой стрелке относительно оси, индекса которой нет в его обозначении (в нашем случае относительно оси z).
положительно, если оно стремится повернуть элемент по часовой стрелке относительно оси, индекса которой нет в его обозначении (в нашем случае относительно оси z).
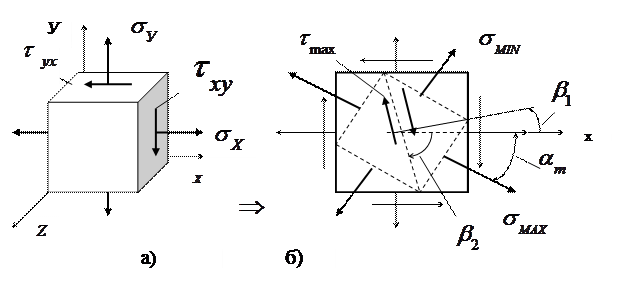
Рис. 3.1
Положение главной площадки к оси х определяется углом 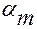 , значение которого вычисляем по формуле (2.3):
, значение которого вычисляем по формуле (2.3):
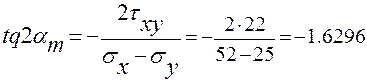 .
.
Откуда
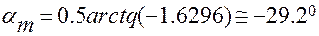 .
.
При 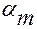 > 0 элемент с главными площадками повернут отно-сительно исходного элемента против хода часовой стрелки,
> 0 элемент с главными площадками повернут отно-сительно исходного элемента против хода часовой стрелки,
при 
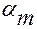 < 0 – в противоположном направлении.
< 0 – в противоположном направлении.
В нашем случае элемент с главными площадками изображен пунктиром на рис. 3.1,б.
Значения главных напряжений, действующих по найденным гла-вным площадкам, определяются по формуле (2.2):
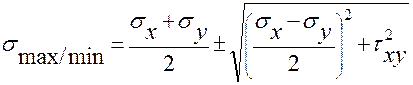 .
.
Вычисления по этой формуле приводят к следующим результа-там:
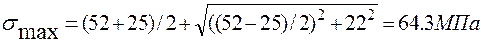 ,
,
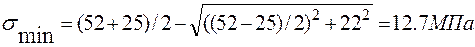 .
.
Эти же главные напряжения можно также получить, используя формулу для определения нормальных напряжений в площадках наклоненных к оси х под углом α
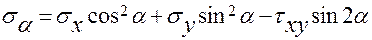 ,
,
в которую следует поочередно подставить кроме заданных напря-жений  ,
, 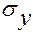 и
и 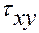 значения углов:
значения углов:
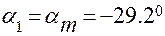 ;
; 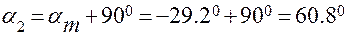 .
.
При 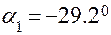 имеем:
имеем:
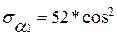
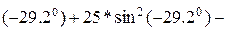 22*sin
22*sin 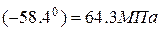 .
.
При 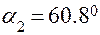 имеем:
имеем:
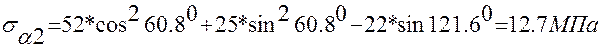 .
.
Учитывая принятое соотношение между главными напряжениями
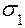 ≥
≥ 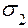 ≥
≥ 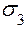 , получаем:
, получаем:
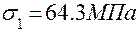 ;
; 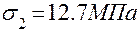 ;
; 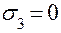 .
.
Далее следует показать найденные напряжения на элементе (см. рис. 3.1,б). При первом варианте определения главных напряжений надо большее из найденных напряжений 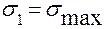 показывать на главных площадках, ориентированных к тем угловым точкам исходного элемента, к которым сходятся касательные напряжения. В случае использования второго варианта расчета трудностей с рас-становкой главных напряжений нет.
показывать на главных площадках, ориентированных к тем угловым точкам исходного элемента, к которым сходятся касательные напряжения. В случае использования второго варианта расчета трудностей с рас-становкой главных напряжений нет.
Инвариантность суммы нормальных напряжений, действующих во взаимно перпендикулярных площадках двух разных по углу поворота элементов, проверяется по формуле:
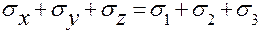 = const.
= const.
В нашей задаче
52+ 25 +0 = 64.3 +12.7 + 0 = 77,
что подтверждает правильность вычислений.
Значение максимального касательного напряжения в плоскости, параллельной плоскости хоу, вычислим по формуле:
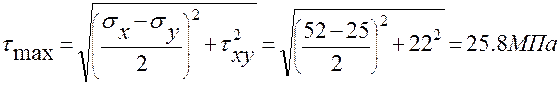 .
.
Это же значение 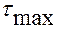 можно получить через главные напряжения, лежащие в плоскости, параллельной плоскости хоу. В рассматриваемом примере такими являются
можно получить через главные напряжения, лежащие в плоскости, параллельной плоскости хоу. В рассматриваемом примере такими являются
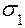 = 64.3 МПа и
= 64.3 МПа и 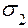 =12.7 МПа.
=12.7 МПа.
Тогда найдем
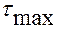 = (64.3 – 12.7)/2 = 25.8МПа.
= (64.3 – 12.7)/2 = 25.8МПа.
Площадки, по которым действуют эти напряжения, наклонены к главным площадкам на угол 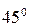 . Нормали к площадкам с
. Нормали к площадкам с 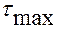 составят с осью х угол:
составят с осью х угол:
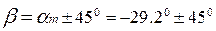 ;
;
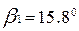 (повернуть против хода часовой стрелки);
(повернуть против хода часовой стрелки);
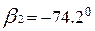 (повернуть по ходу часовой стрелки).
(повернуть по ходу часовой стрелки).
При необходимости определения максимальных касательных напряжений без ограничения плоскости их расположения они нахо-дятся по формуле:
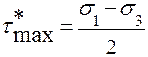
справедливой для любого вида напряженного состояния. В нашем примере

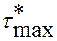
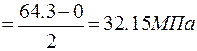 .
.
Это напряжение действует в площадке, равно наклоненной к площадкам 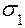 (максимального) и
(максимального) и 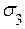 (минимального) из главных напряжений.
(минимального) из главных напряжений.
ЗАДАЧА 3.2.
Ломаный брус (рис. 3.2) загружен силами 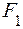 = 2кН,
= 2кН, 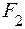 = 1кН, равномерно распределенной нагрузкой интенсивностью q = 1 кН/м и моментом Т =1 кНм. Размеры бруса a = 1 м, с = 1 м.
= 1кН, равномерно распределенной нагрузкой интенсивностью q = 1 кН/м и моментом Т =1 кНм. Размеры бруса a = 1 м, с = 1 м.
Требуется подобрать:
на участке АВ – размер диаметра круглого сплошного сечения;
на участке ВС - размеры h и b ( h = 2 b ) прямоугольного се-чения. Материал бруса - сталь  ,
, 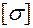 = 160 МПа.
= 160 МПа.
При расчетах использовать теорию прочности максимальных касательных напряжений.
Построение эпюр изгибающих 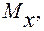
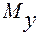 и крутящего
и крутящего 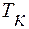 моментов. В сечениях бруса под действием приложенных внешних сил и моментов возникают изгибающие и крутящий моменты, поперечные и нормальная силы. При расчете на проч-ность таких брусьев влиянием поперечных и нормальных сил обычно пренебрегают. Поэтому для рассматриваемого примера эпюры поперечных и нормальных сил не строим.
моментов. В сечениях бруса под действием приложенных внешних сил и моментов возникают изгибающие и крутящий моменты, поперечные и нормальная силы. При расчете на проч-ность таких брусьев влиянием поперечных и нормальных сил обычно пренебрегают. Поэтому для рассматриваемого примера эпюры поперечных и нормальных сил не строим.
Приступая к решению задачи, прежде всего, необходимо на каждом участке бруса (см. рис. 3.2,а) показать скользящую систему координат xyz в сечениях А и В (ось z должна быть направлена вдоль оси бруса).
Далее, делая обход со свободного конца бруса по его контуру (переходя от одного участка к следующему участку бруса, наблюдатель не должен пересекать ось z ), записываем выражения изгибающих и крутящих моментов для текущих сечений каждого участка бруса.
Участок АМ:
(плоскость zy) 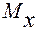 = 0; (плоскость zx)
= 0; (плоскость zx) 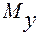 = q
= q 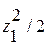 ;
; 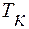 = Т.
= Т.
Участок МВ:
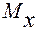 =
= 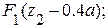
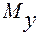 =q(0.4a)(
=q(0.4a)( 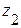 -0.2a);
-0.2a); 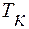 = Т.
= Т.
Участок ВЕ:
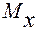 =
= 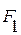 (0,6a);
(0,6a); 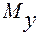 = T + q( 0,4 a)
= T + q( 0,4 a) 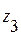 ;
; 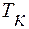 = - q(0,4a)(0,8a).
= - q(0,4a)(0,8a).
Участок ЕС:
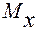 =
= 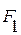 (0,6a);
(0,6a); 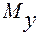 = T+q (0,4a)
= T+q (0,4a) 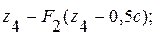
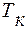 = - q(0,4a)(0,8a).
= - q(0,4a)(0,8a).
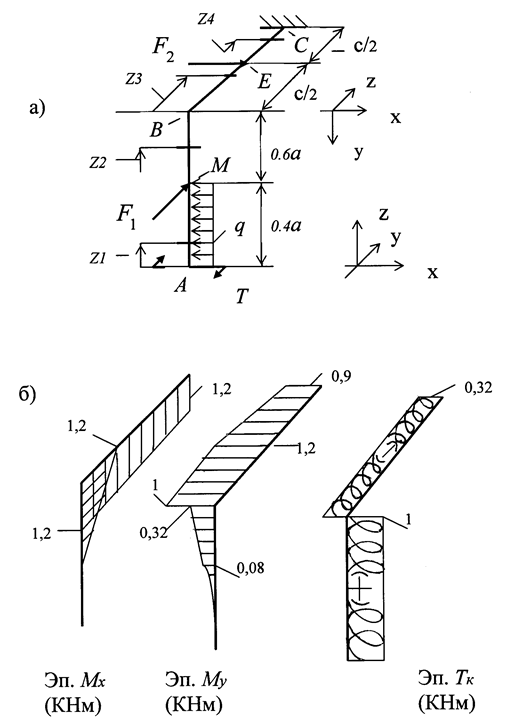
Рис. 3.2
По полученным уравнениям, задаваясь значениями координаты z, подсчитываем величины ординат 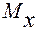 ,
, 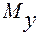 ,
, 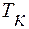 в начале и конце каждого участка и строим соответствующие эпюры (рис. 3.2,б). Напоминаем, что эпюры изгибающих моментов строим со стороны сжатых волокон бруса, а эпюры крутящих моментов можно строить в любой плоскости, но обязательно следует указывать знаки.
в начале и конце каждого участка и строим соответствующие эпюры (рис. 3.2,б). Напоминаем, что эпюры изгибающих моментов строим со стороны сжатых волокон бруса, а эпюры крутящих моментов можно строить в любой плоскости, но обязательно следует указывать знаки.
Выявление наиболее нагруженных сечений участков бруса.
На каждом участке опасное сечение или несколько таких сечений, если есть сомнение, устанавливают путем анализа эпюр изгибающих и крутящих моментов. В рассматриваемом примере из построенных эпюр (см. рис. 3.2,б) следует, что на участке бруса АВ таким сечением является сечение В, а на участке ВС - сечение Е. Для проведения дальнейших расчетов рекомендуем опасные сечения изображать отдельно и в них показывать действующие изгибающие и крутящий моменты, а также соответствующие им эпюры нормальных и касательных напряжений.
Расчет диаметра круглого поперечного сечения бруса – на участке АВ.
На рис. 3.3,а изображено опасное сечение В. Показаны изгибающие моменты 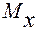 = 1,2 кНм,
= 1,2 кНм, 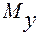 = 0,32 кНм и крутящий момент
= 0,32 кНм и крутящий момент 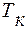 = 1 кНм.
= 1 кНм.
Для бруса круглого или кольцевого поперечного сечения любая диаметральная ось является главной, поэтому при действии двух изгибающих моментов он не испытывает косого изгиба. Моменты могут быть приведены к суммарному
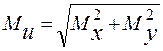 .
.
Из эпюр нормальных 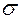 и касательных
и касательных 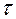 напряжений (рис. 3.3,б) следует, что наиболее опасными точками в рассматриваемом сечении будут точки 1 и 2. Материал бруса испытывает напряженное состояние растяжения - сжатия и сдвига, т.е. находится в условиях сложного напряженного состояния. Оценку прочности в этом случае необходимо проводить с применением одной из теорий прочности.
напряжений (рис. 3.3,б) следует, что наиболее опасными точками в рассматриваемом сечении будут точки 1 и 2. Материал бруса испытывает напряженное состояние растяжения - сжатия и сдвига, т.е. находится в условиях сложного напряженного состояния. Оценку прочности в этом случае необходимо проводить с применением одной из теорий прочности.
Эквивалентное напряжение для такого случая двухосного напряженного состояния по теории максимальных касательных напряжений подсчитывается (2.9):
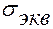 =
= 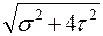 .
.
Зная, что для круглого сечения полярный момент сопротивления 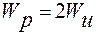 (
( 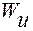 - момент сопротивления сечения при изгибе), формулу (2.9), можно записать в виде:
- момент сопротивления сечения при изгибе), формулу (2.9), можно записать в виде:
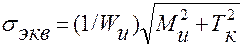 , (3.1)
, (3.1)
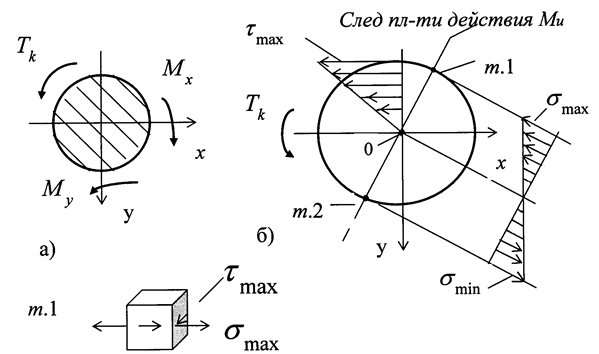
Рис. 3.3
где 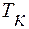 и
и 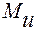 - крутящий и изгибающий моменты.
- крутящий и изгибающий моменты.
Подбор безопасных размеров сечения (проектный расчет) проводится следующим образом. Для опасной точки вычисляют значение эквивалентного напряжения, в которое входит и неизвестная величина момента сопротивления сечения 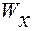 , выраженная через размеры сечения. Приравнивая эквивалентное напряжение допускаемому
, выраженная через размеры сечения. Приравнивая эквивалентное напряжение допускаемому
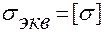 , (3.2)
, (3.2)
вычисляют величину 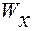 , а, следовательно, и безопасные размеры сечения.
, а, следовательно, и безопасные размеры сечения.
Вернемся к рассматриваемому примеру. Из условия задачи следует, что материал бруса пластичный материал – сталь, одинаково сопротивляющаяся растяжению – сжатию. По теории прочности максимальных касательных напряжений эквивалентное напряжение для самой опасной точки 1 сечения определяется по формуле (3.1):
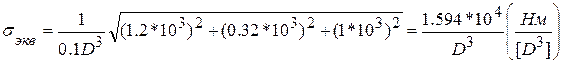 ,
,
где было принято 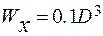 .
.
Учитывая (3.2), определим безопасную величину диаметра круг-лого сечения
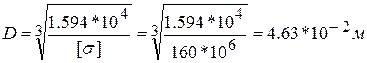
Округляя найденное значение в миллиметрах до ближайшего числа из стандартного ряда (см. приложение 2 , с.114) принимаем
D = 48 мм.
Расчет размеров прямоугольного поперечного сечения бруса – на участке ВС.
Рассматривая участок ВС бруса прямоугольного сечения, необходимо показать изгибающие и крутящий моменты, действующие в опасном сечении Е, а также соответствующие им эпюры напряжений (рис. 3.4).
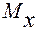 = 1,2 кНм ;
= 1,2 кНм ; 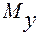 = 1,2 кНм;
= 1,2 кНм; 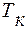 = 0,32 кНм.
= 0,32 кНм.
Опасными точками сечения могут быть точки 1, 2. 3, т.к. согласно эпюрам, в этих точках напряжения достигают своих экстремальных значений.
В точке 1 складываются нормальные напряжения 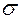 от двух изгибающих моментов
от двух изгибающих моментов 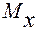 ,
, 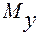 и возникает одноосное напря-женное состояние:
и возникает одноосное напря-женное состояние:
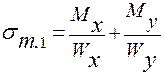 ,
,
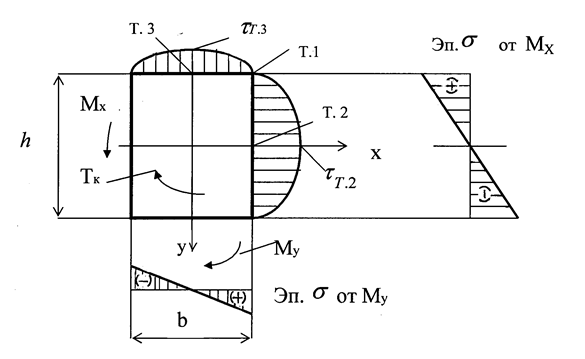
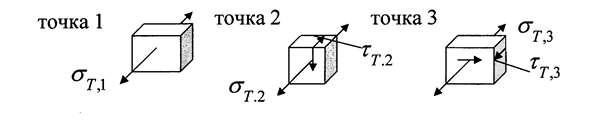
Рис. 3.4
где 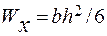 ,
, 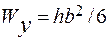 - моменты сопротивления сечения на изгиб относительно осей х и у.
- моменты сопротивления сечения на изгиб относительно осей х и у.
Учитывая, что h = 2 b , получим:
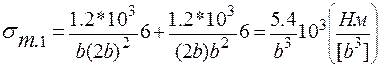 .
.
В точке 2 возникают нормальные напряжения 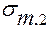 от момента
от момента 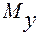 и касательные
и касательные 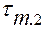 напряжения от крутящего момента
напряжения от крутящего момента 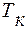 :
:
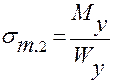 ;
; 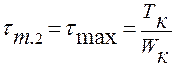 .
.
Здесь - 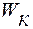 момент сопротивления сечения на кручение
момент сопротивления сечения на кручение 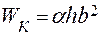 , где
, где 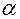 - коэффициент, определяемый по таблицам в зависимости от отношения h/b (см., например, [1], стр. 125, табл. 2.1). Так, для h / b = 2,
- коэффициент, определяемый по таблицам в зависимости от отношения h/b (см., например, [1], стр. 125, табл. 2.1). Так, для h / b = 2, 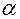 = 0.246.
= 0.246.
Напряженное состояние в данной точке двухосное (растяжение и сдвиг). Эквивалентное напряжение по теории прочности максимальных касательных напряжений следует находить по формуле (2.9):
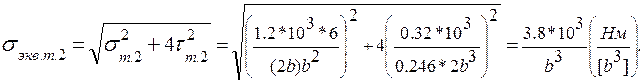 Аналогично вычисляем нормальные и касательные напряжения для точки 3:
Аналогично вычисляем нормальные и касательные напряжения для точки 3: 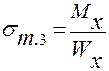 ;
; 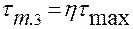 ,
,
где 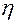 - коэффициент, определяемый так же, как и коэффициент
- коэффициент, определяемый так же, как и коэффициент 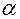
Для h/b = 2 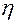 = 0.796.
= 0.796.
Эквивалентное напряжение для этой точки:

После вычисления значений 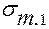 ,
, 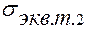 ,
, 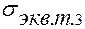 следует вы-брать наибольшее из них, приравнять его допускаемому напряже-нию
следует вы-брать наибольшее из них, приравнять его допускаемому напряже-нию 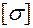 = 160МПа (3.2) и определить размеры сечения b и h .
= 160МПа (3.2) и определить размеры сечения b и h .
В рассматриваемом примере
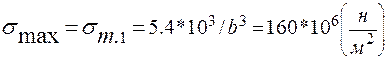 .
.
Откуда b = 32.3 мм.
Используя приложение 2 (с.114), принимаем b =35 мм, h = 70 мм.
Пример. Для показанного на рис. 3.5 стального пространствен-ного ломаного бруса, имеющего круглое поперечное сечение диаметром d =0,05 м, используя четвертую теорию прочности, найти допускаемое значение силы F. В расчетах принять l = 0,5 м, [ 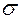 ] = 160 МПа.
] = 160 МПа.
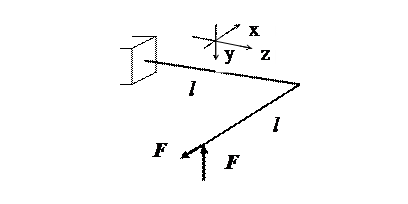
Рис. 3.5
Решение
Брус статически определимый. На рис. 3.6 построены эпюры изгибающих МХ , МУ и крутящих моментов ТК.
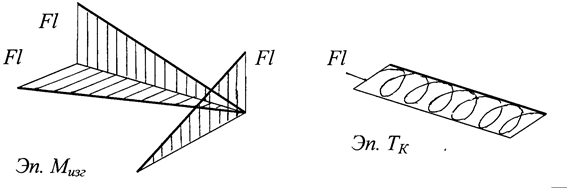
Рис. 3.6
Из анализа эпюр следует, что опасное сечение в заделке. В этом сечении значения изгибающих и крутящих моментов равны:
MX = Fl; MY = Fl; ТК = Fl.
При расчете удобно пользоваться эквивалентным изгибающим моментом МЭКВ, выражение которого определяется по формуле (энергетическая теория прочности):
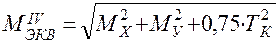 .
.
Используя условие прочности:
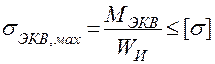 ,
,
Получим:
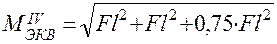 = 1,66 Fl.
= 1,66 Fl.
Зная WИ = 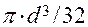 , имеем:
, имеем:
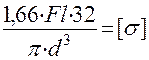 .
.
Откуда, подставляя заданные значения l = 0,5 м, d = 5·10-2 м, [ 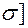 , находим допускаемое значение силы FДОП = 2,36 кН.
, находим допускаемое значение силы FДОП = 2,36 кН.
ЗАДАЧА 3.3.
Тонкостенная длинная замкнутая трубка (рис. 3.7,а) толщиной стенки 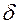 = 2 мм и средним диаметром D = 40 мм находится под действием внутреннего давления p = 5 МПа и моментов М = 50 Нм, Т = 50 Нм. Требуется определить коэффициент запаса трубки. Материал трубки – сталь У-8 незакаленная
= 2 мм и средним диаметром D = 40 мм находится под действием внутреннего давления p = 5 МПа и моментов М = 50 Нм, Т = 50 Нм. Требуется определить коэффициент запаса трубки. Материал трубки – сталь У-8 незакаленная 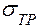 = 250 МПа,
= 250 МПа, 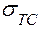 = 430 МПа.
= 430 МПа.
Определение напряжений в поперечных и продольных сечениях трубки. Решение задачи следует начинать с определения нормальных и касательных напряжений, возникающих в попе-речных и продольных сечениях трубки под действием прило-женных к ней внешних нагрузок. При этом следует рассматривать сечения, расположенные на достаточном удалении от концов трубки, где возникает однородное по ее продольной оси напряженное состояние. Для рассматриваемой трубки таким сечением является сечение 1-1.
Используя принцип независимости действия сил, определим напряжения в этом сечении отдельно от М , Т , а также внутреннего давления р .
От действия внешнего момента М в поперечных сечениях трубки возникает изгибающий момент 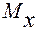 = М . При этом максимальные
= М . При этом максимальные 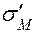 и минимальные
и минимальные 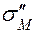 нормальные напряжения будут в точках С и В поперечного сечения трубки (рис. 3.7,б), и их следует определять по формулам:
нормальные напряжения будут в точках С и В поперечного сечения трубки (рис. 3.7,б), и их следует определять по формулам:
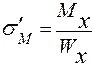 ;
; 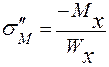 , где
, где 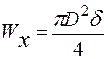 - момент сопротивле-ния поперечного сечения трубки при изгибе.
- момент сопротивле-ния поперечного сечения трубки при изгибе.
Тогда 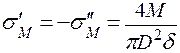 .
.
Внешний (скручивающий) момент Т вызывает в поперечных сечениях трубки крутящий момент 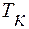 = Т.
= Т.
Касательные напряжения 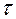 равномерно распределены по толщине стенки (рис. 3.7,с), и их следует подсчитывать по формуле:
равномерно распределены по толщине стенки (рис. 3.7,с), и их следует подсчитывать по формуле: 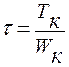 ,
,
где 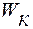 - момент сопротивления сечения трубки при кручении.
- момент сопротивления сечения трубки при кручении.
Величину 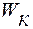 необходимо определять как для тонкостенного кольца:
необходимо определять как для тонкостенного кольца: 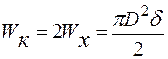 . Тогда:
. Тогда:
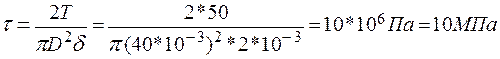 .
.
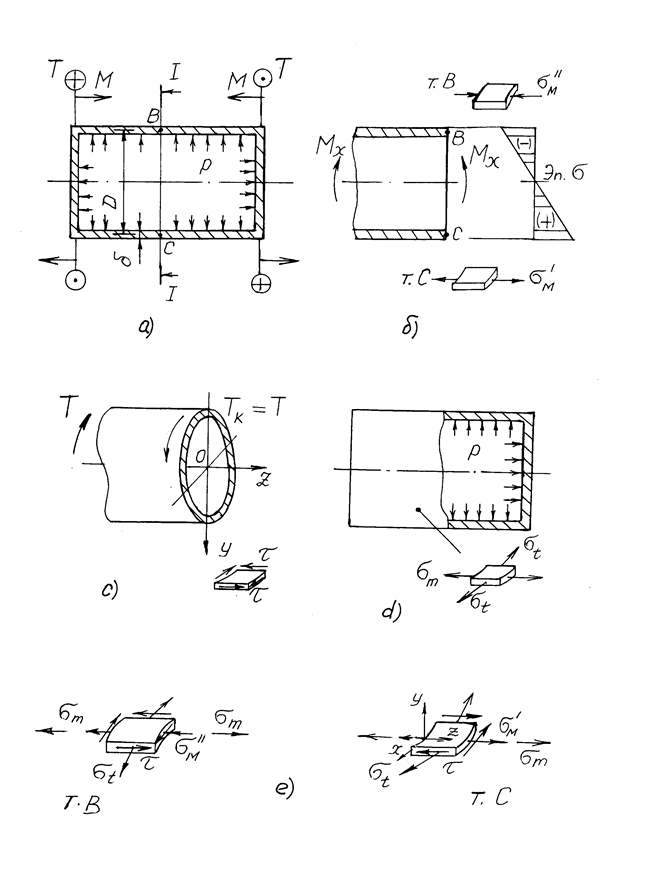
Рис.3.7
Под действием внутреннего давления р в продольных и поперечных сечениях трубки возникают нормальные напряжения 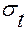 и
и 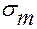 (рис. 3.7,д).
(рис. 3.7,д).
Напряжение 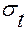 определим из формулы Лапласа:
определим из формулы Лапласа:
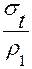 +
+ 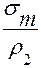 =
= 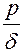
 ,
,
где 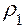 и
и 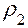 - радиусы кривизны поверхности трубки по направлениям действия напряжений
- радиусы кривизны поверхности трубки по направлениям действия напряжений 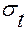 и
и 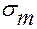 .
.
Принимая 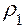 =D/2 ;
=D/2 ; 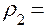 ∞, находим:
∞, находим:
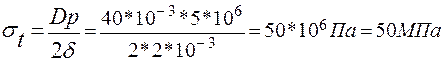 .
.
Напряжение 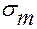 установим следующим образом.
установим следующим образом.
Действующее на крышку трубки давление p вызывает растя-жение трубки в осевом направлении силой 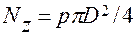 .
.
Величину напряжения 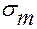 получим, разделив значение этой силы на площадь поперечного сечения трубки A =
получим, разделив значение этой силы на площадь поперечного сечения трубки A = 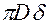 ::
::
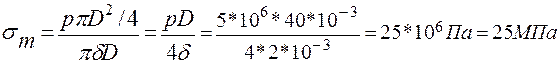 .
.
После определения напряжений в стенках трубки от каждого внешнего силового фактора следует провести анализ возникающего напряженного состояния в точках рассматриваемого поперечного сечения 1–1 (см. рис. 3.7,с).
Анализ напряженного состояния материала трубки
В рассматриваемом поперечном сечении трубки 1-1 касатель-ные 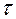 и нормальные
и нормальные 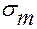 ,
, 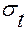 напряжения одинаковы во всех точках, а нормальные напряжения
напряжения одинаковы во всех точках, а нормальные напряжения 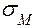 от изгибающего момента достигают экстремальных значений в точках С и В сечения. Значит опасными точками могут быть точки С и В (рис. 3.7,е).
от изгибающего момента достигают экстремальных значений в точках С и В сечения. Значит опасными точками могут быть точки С и В (рис. 3.7,е).
Точка С.
Нормальные напряжения:
- по оси трубки 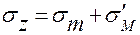 = 25+20 = 45МПа.
= 25+20 = 45МПа.
- в окружном направлении  = 50МПа.
= 50МПа.
Касательные напряжения: 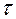 = 10МПа.
= 10МПа.
Точка В.
Нормальные напряжения:
- по оси трубки 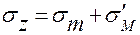 = 25-20 = 5МПа;
= 25-20 = 5МПа;
- в окружном направлении  = 50МПа.
= 50МПа.
Касательные напряжения: 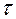 = 10МПа.
= 10МПа.
Напряженное состояние рассматриваемых элементов точек – двухосное, т.к. напряжения в радиальном направлении можно принять 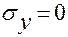 .
.
Сравнение полученных величин напряжений показывает, что наиболее опасной точкой поперечного сечения трубки является точка С. Максимальное и минимальное нормальные напряжения в главных площадках для этой точки находятся по формуле 2.2 (см. решение задачи № 3.1 c.62):
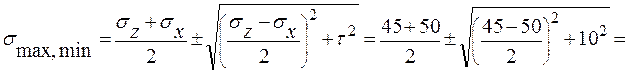
=(47.5± 10.3)МПа,
или
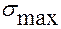 = 57.8МПа,
= 57.8МПа, 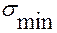 = 37.2МПа.
= 37.2МПа.
Главные напряжения для рассматриваемого элемента записыва-ются в алгебраическом порядке ( 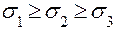 ) следующим образом:
) следующим образом:
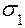 = 57,8МПа,
= 57,8МПа, 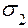 = 37,2МПа ,
= 37,2МПа , 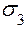 = 0.
= 0.
Учитывая заданный материал трубки ( 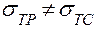 ), находим эквивалентное напряжение для рассматриваемой точки по теории прочности Мора (2.8):
), находим эквивалентное напряжение для рассматриваемой точки по теории прочности Мора (2.8):
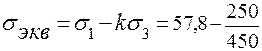 ·0 = 57,8МПа.
·0 = 57,8МПа.
Определение коэффициента запаса
Из выше проведенных расчетов следует, что наиболее опасной точкой поперечного сечения трубки является точка С. В ней
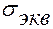 = 57,8МПа.
= 57,8МПа.
Коэффициент запаса по текучести в этой точке определим по следующей формуле:
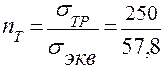 = 4,33.
= 4,33.
Если нельзя сразу указать опасную точку сечения, то следует провести расчет коэффициента запаса для каждой из точек С и В отдельно и выбрать из них наименьший.
| |
Для показанного на рис. 3.8 пространственного ломаного бруса, имеющего круглое поперечное сечение и загруженного силой F = 1кН, подобрать диаметр d сечения и найти угол поворота сечения А относительно главной центральной оси х.
Дано: l = 1 м, 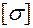 = 160 МПа, E = 2·105 МПа, G=0,8 ·105 МПа.
= 160 МПа, E = 2·105 МПа, G=0,8 ·105 МПа.
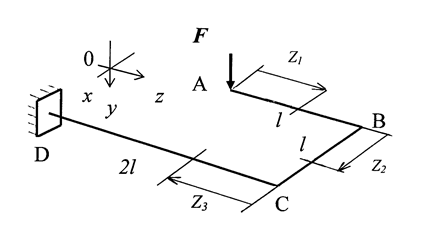
Рис. 3.8
Решение
Построим эпюры изгибающих и крутящих моментов, возника-ющих в сечениях бруса от приложенной нагрузки.
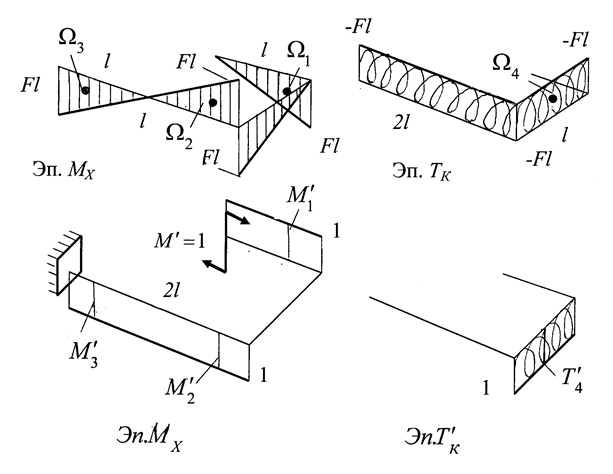
| |
Рис. 3.9,а
Начинаем обход со свободного конца бруса.
Участок АВ ( 0 ≤ z1 ≤ l ):
рассматриваемая отсеченная часть бруса показана на рис. 3.9,б;
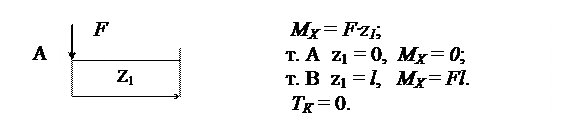
Рис. 3.9,б
Участок ВС ( 0 ≤ z2 ≤ l ):
отсеченная часть бруса дана на рис. 3.9,в;
переносим силу F из точки А в узел В. Тогда на стержень ВС будут действовать сила F и момент Fl, приложенные в начальном сечении В этого стержня;.

Рис. 3.9,в
MX = F·z2;
т. В z2 = 0, MX = 0; т. С z2 = l, MX = Fl.
ТК = - Fl.
Участок CD ( 0 ≤ z3 ≤ 2l ):
отсеченная часть бруса изображена на рис. 3.9,г;
аналогично вышерассмотренному участку переносим силу F и момент Fl из узла В в узел С – начальное сечение стержня СD.
На участке CD будут действовать изгибающий момент Fl, крутящий момент Fl и поперечная сила F:
MX = Fl - F·z3;
т.С z3 = 0, MX = Fl; т. D z3 = l, MX = -Fl;
ТК = -Fl.
Полученные выражения и значения для МХ, МУ и ТК позволяют построить эпюры (рис. 3.9,а).
Анализ построенных эпюр показывает, что опасными сечениями бруса являются узловые сечения С стержней ВС и CD, а также сечение D стержня DC, где действуют наибольшие значения изгибающих и крутящего моментов и равные Fl.
Подбираем размер диаметра d поперечного сечения бруса.
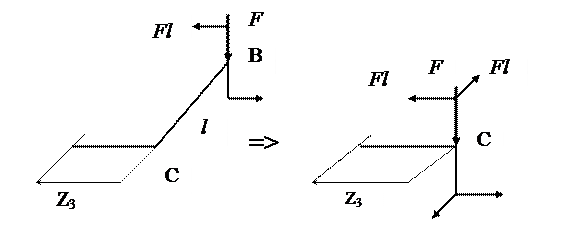
Рис. 3.9,г
На рис. 3.10 показаны общая расчетная схема этих сечений с действующими МХ и ТК, а также элемент напряженного состояния наиболее опасной точки сечения – т. 1. В этой точке будут действовать одновременно нормальные и касательные напряжения. Элемент находится в плоском наряженном состоянии. Поэтому для оценки прочности воспользуемся одной из теорий прочности. По теории прочности максимальных касательных напряжений, применяемой для материалов, у которых пределы текучести материала при растяжении и сжатии одинаковы, эквивалентное напряжение подсчитывается по формуле (2.9):
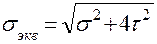 .
.
Для круглого поперечного сечения напряжения равны:
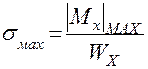 ,
, 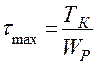 .
.
Зная, что WP = 2WX = 0,2 d3 и введя эквивалентный изгибающий момент
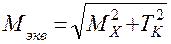 ,
,
Запишем выражение для 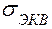 в виде
в виде
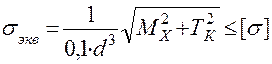 .
.
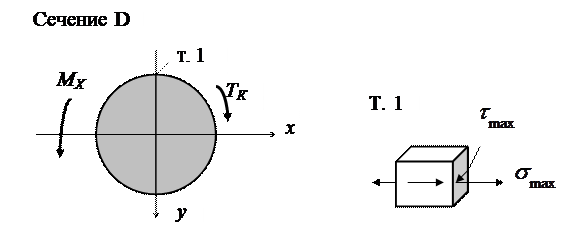
Рис. 3.10
Откуда 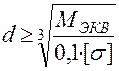 .
.
После подстановки числовых значений, найдем d = 4,5·10-2 м.
Определим угол поворота сечения А относительно оси х. для этого приложим в сечении А относительно этой оси момент 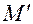 =1.
=1.
Эпюры изгибающих и крутящих моментов в брусе от этого момента показаны на рис. 3.9.
Вычисляем интеграл Мора:

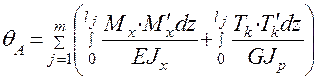 =
=
= 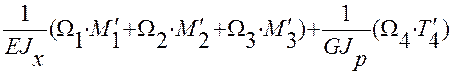 =
=
= 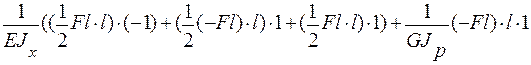 =
=
= 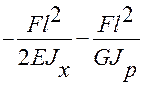 = - 0,04 рад
= - 0,04 рад
Тема 4. РАСЧЕТ ВАЛА НА СТАТИЧЕСКУЮ ПРОЧНОСТЬ И СОПРОТИВЛЕНИЕ УСТАЛОСТИ
В данной задаче студент должен решить вопросы, которые составляют следующие три раздела:
- проектировочный расчет вала на статическую прочность;
- конструирование вала;
- проверочный расчет вала на усталостную прочность.
Дата: 2016-10-02, просмотров: 653.