Разность между числом неизвестных реакций связей (n) и числом независимых уравнений статики (k), которые могут быть составлены для рассматриваемой системы, называется степенью статической неопределимости (S). Например, для балки, показанной на рис. 1.5,а, получим
S = 4 - 3 = 1,
где n = 4 – число реакций в шарнирных опорах,
k = 3 – количество уравнений равновесия статики.
ЗАДАЧА 1.1. Для рамы с жестко закрепленным одним концом и загруженной, как показано на рис. 1.6,a, построить эпюру изги-бающих моментов и найти угол поворота узла С.
Решение
Опора А рамы является заделкой (защемлением). В ней возникают три реакции – опорный момент, вертикальная и гори-зонтальные реакции. Имеются три уравнения статики, поэтому данная рама статически определимая. В подобных рамах можно не определять значения опорных реакций, если построение эпюры изгибающих моментов вести от свободного конца рамы (т. Е). На рис. 1.6,б показаны места рассечения участков рамы определяемыми поперечными сечениями с координатами z1, z2, z3 и z4.
Участок ЕD ( 0 ≤ z1 ≤ l ).
В соответствии с методом сечений отсекаем сечением на рассто-янии z1 от свободного конца рамы (т. Е) часть рамы, которую показываем отдельно (рис. 1.6,в). В сделанном поперечном сечении могут действовать внутренние силовые факторы: Nz -нормальная сила; Qу –поперечная сила; Мх –изгибающий момент.
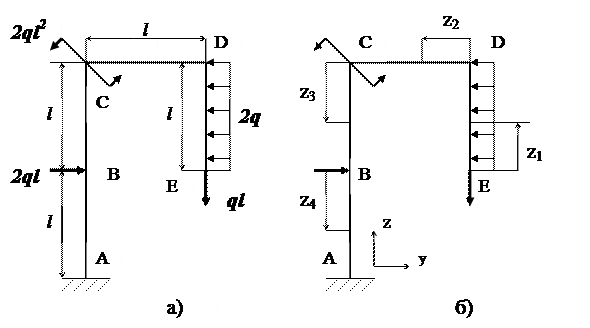
Рис. 1.6
По условию задачи требуется определить только МХ. Его значения найдем из условия равновесия отсеченной части 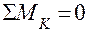 , где к – центр тяжести текущего поперечного сечения стержня рамы:
, где к – центр тяжести текущего поперечного сечения стержня рамы:
|

Участок CD ( 0 ≤ z2 ≤ l ).
Отсеченная часть рамы показана на рис. 1.6.г. Из соображений упрощения рисунков здесь и далее при показе отсеченных частей рамы будем опускать изображения в текущем поперечном сечении NZ, QY и MX. Также для упрощения расчетов будем переносить на-грузки, приложенные на ранее рассмотренном участке (участке ED), в начало следующего участка рамы (узел D). Так, распределенную нагрузку интенсивностью 2q приводим к узлу D в виде сосредоточенной силы 2ql (рис. 1.6.д) и пары ql2. Вертикальную силу ql, приложенную в крайнем сечении Е переносим вдоль линии действия (по вертикали) к узлу D.
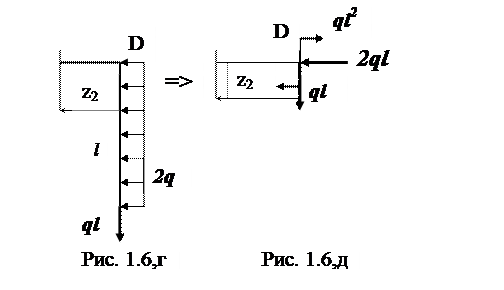
Рассматривая отсеченную часть, изображенную на рис. 1.6,д, мо-жем записать:
Mx = ql2 + ql·z2.
Значения МХ в крайних поперечных сечениях (точках) участка DC:
т. D z2 = 0, MX = ql2; т. С z2 = l, Mx = 2ql2.
Переносим силы, действующие на участок ED, в точку D. В сечении D участка CD будут действовать, взамен распределенной нагрузки 2ql, момент ql2 и сила 2ql, а также сила ql, перенесенная из точки Е.
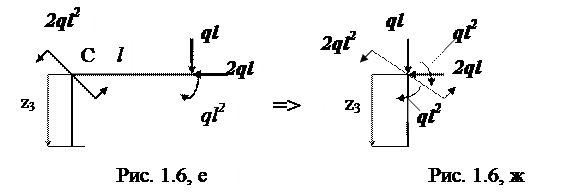
Участок ВС ( 0 ≤ z3 ≤ l ):
Отсеченная часть рамы дана на рис. 1.6,е, а ее эквивалентный вид с приведенными нагрузками в начальном сечении С показан на рис. 1.6,ж. Выражение для изгибающего момента в текущем поперечном сечении с координатой z3 имеет вид:
Значения МХ в крайних сечениях участка:
т. C z3 = 0; MX = 0; т. В z3 = l; MX = 2ql2
Участок ВА ( 0 ≤ z4 ≤ l ):
Поступая аналогичным образом, как и для вышерассмотренных трех участков, изобразим отсеченную часть участка с эквивалентными нагрузками в начальном сечении В (рис. 1.6,з) и запишем выражение для изгибающего момента в текущем сечении с координатой z4.
|

По результатам вычислений строим эпюру изгибающих моментов (рис. 1.7,а). За нулевые линии принимаются продольные оси стержней, а значения ординат МХ откладываем на сжатых волокнах стержней без указания знака.
Для проверки построенной эпюры вырезаем узлы D и С рамы (рис. 1.7,б, в). В поперечных сечениях стержней, соединяемых в узлы, показываем действующие изгибающие моменты, значения которых снимаем с эпюры МХ (см. рис. 1.7,а) Кроме того в узле С следует изобразить внешний момент 2ql2. Далее составляем уравнения равновесия узлов:
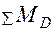 =ql2 – ql2 = 0;
=ql2 – ql2 = 0;  = 2ql2 – 2ql2 = 0.
= 2ql2 – 2ql2 = 0.
Равенство сумм моментов нулям показывает, что узлы находятся в равновесии.
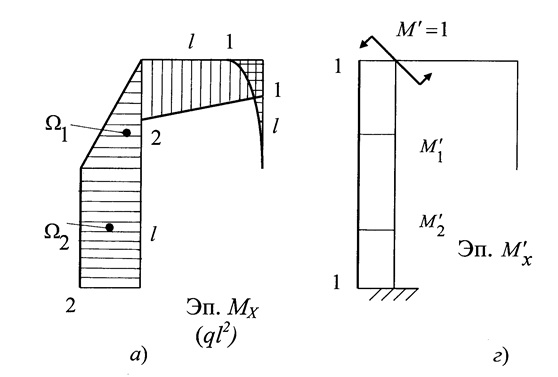
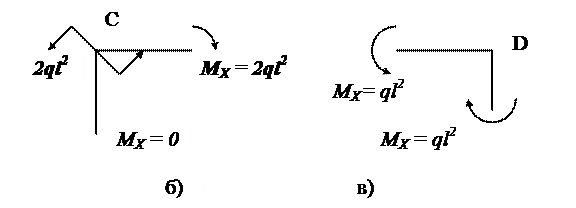
Рис. 1.7
По формуле Мора с использованием правила Верещагина вычислим угол поворота угла С.
Снимаем с рамы все нагрузки и в точке С прикладываем момент 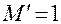 (рис. 1.7,г). Строим от него эпюру (Эп.
(рис. 1.7,г). Строим от него эпюру (Эп. 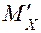 ). Перемножаем эпюры МХ и
). Перемножаем эпюры МХ и 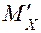 . Участков перемножения два: АВ и ВС.
. Участков перемножения два: АВ и ВС.
Показываем центры тяжести простейших площадей 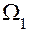 и
и 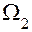 эпюры МХ на участках АВ и ВС перемножения эпюр, а на эпюре
эпюры МХ на участках АВ и ВС перемножения эпюр, а на эпюре 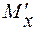 соответствующие моменты
соответствующие моменты 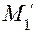 и
и 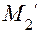 .
.
Угол поворота узла С равен:
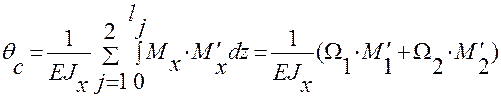 =
=
=  .
.
Знак плюс в ответе означает, что узел С поворачивается в на-правлении момента 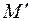 = 1, т.е. против часовой стрелки.
= 1, т.е. против часовой стрелки.
ЗАДАЧА 1.2.Для показанной на рис. 1.8 рамы построить эпюры изгибающих моментов МХ и поперечных сил QY, а также найти угол поворота поперечного сечения А, связанного с шарнирно- неподвижной опорой.
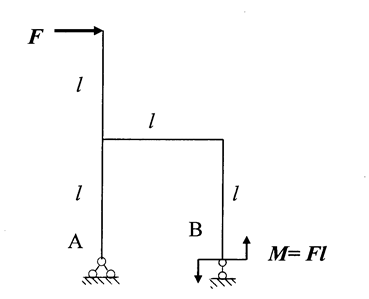
Рис. 1.8
Решение
Обозначим границы участков нагружения рамы буквами C, D, E и покажем реакции XA, YA, YB, возникающие в опорах А и В соответственно (рис. 1.9,а).
Значения опорных реакций найдем из уравнений равновесия рамы в целом в системе координат хоу (см. рис. 1.9,а):
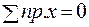 ; - ХA + F = 0 ; => ХA = F;
; - ХA + F = 0 ; => ХA = F;
 А = 0; -F·2l + YB·l + F·l = 0; => YB = F;
А = 0; -F·2l + YB·l + F·l = 0; => YB = F;
 В = 0; -YA·l - F·2l + F·l = 0; = > YA = - F.
В = 0; -YA·l - F·2l + F·l = 0; = > YA = - F.
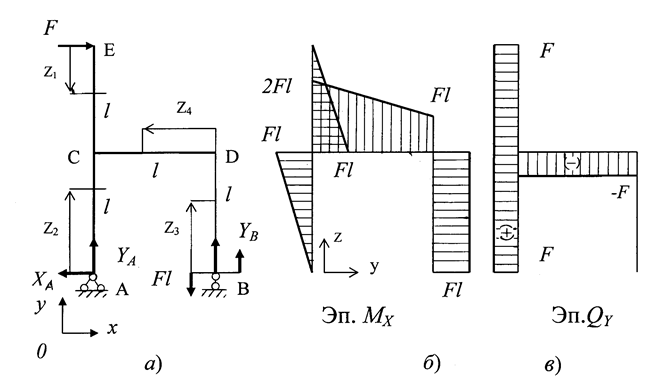
Рис. 1.9
Проверка вертикальных реакций:
∑пр.у = YA + YB = - F + F = 0.
Знак минус в значении реакции YA означает, что она действует в противоположном направлении к принятому ранее.
Определяем выражения для изгибающих моментов МХ и поперечных сил QY на участках (стержнях) рамы.
Участок ЕС (рис. 1.9,г, 0 ≤ Z1 ≤ l ):
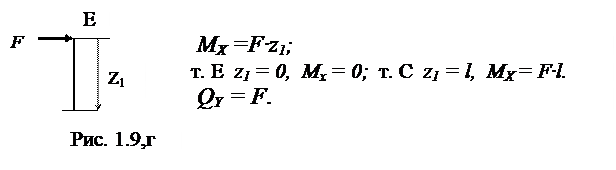
Участок АС (рис. 1.9,д, 0 ≤ z2 ≤ l ):
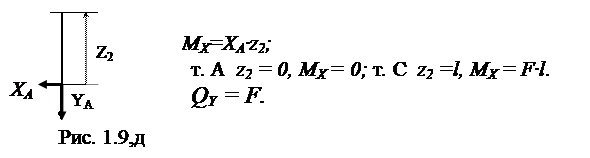
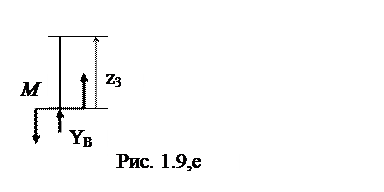
Участок BD (рис. 1.9,е, 0 ≤ z3 ≤ l ):
|
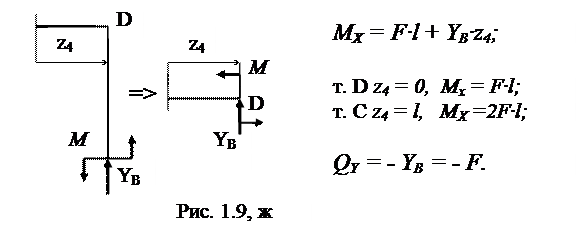
Участок CD (рис. 1.9, ж, 0 ≤ z4 ≤ l ):
Переносим момент М = Fl и силу YB, приложенные в сечении В ранее рассмотренного участка ВD, в начальное сечение участка CD – сечение (узел) D.
По результатам вычислений строим эпюры изгибающих моментов МХ и поперечных сил QY (рис. 1.10,а, б).
Эпюры строим на нулевых линиях, за которые принимаем оси стержней рамы. Значения эпюры QY откладываем с любой стороны от нулевых линий с указанием знаков (см. рис. 1.10,б), а значение эпюры МХ со стороны сжатых волокон без указания знаков (см. рис. 1.10,а).
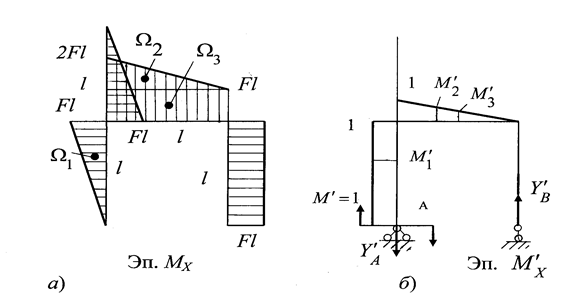
Рис. 1.10
Находим угол поворота сечения А методом Мора. Снимаем все нагрузки, действующие на раму. Прикладываем в т. А момент 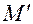 =1. Находим реакции опор и строим эпюру
=1. Находим реакции опор и строим эпюру 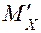 (рис. 1.10,в).
(рис. 1.10,в).
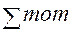 А = 0;
А = 0; 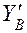 ·l – 1 = 0; =>
·l – 1 = 0; => 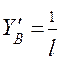 .
.
 B = 0;
B = 0; 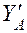 ·l – 1 = 0; =>
·l – 1 = 0; => 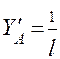 .
.
Угол поворота поперечного сечения А:
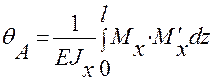 =
= 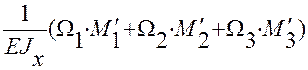 =
=
= 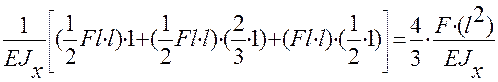 .
.
Сечение А поворачивается в направлении действия момента 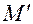 =1, т.е. по часовой стрелке.
=1, т.е. по часовой стрелке.
ЗАДАЧА 1.3.Для показанной на рис. 1.11,а рамы, загружен-ной силой F и моментом М= Fl, определить горизонтальное пере-мещение fгор узла С.
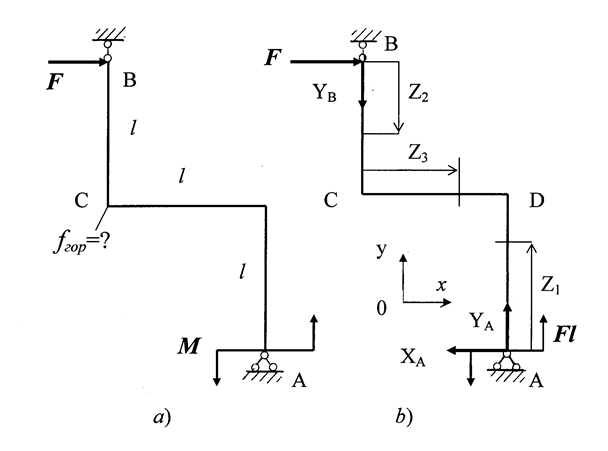
Рис. 1.11
Показываем реакции в опорах (рис. 1.11,б). В опоре В действует одна вертикальная реакция YB, а на опоре А -вертикальная YA и горизонтальная ХА реакции. Таким образом, в опорах рамы возникают три реакции, для определения которых имеются три уравнения статики. Поэтому рама статически определима.
Определяем реакции опор в системе координат хоу (см. рис. 1.11,б):.
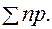 х = 0; - ХA + F = 0; => ХA = F;
х = 0; - ХA + F = 0; => ХA = F;
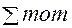 A = 0; - F·2l + YB·l + Fl = 0; => YB = F;
A = 0; - F·2l + YB·l + Fl = 0; => YB = F;
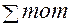 B = 0; Fl + YA·l - XA·2l = 0; => YA = F.
B = 0; Fl + YA·l - XA·2l = 0; => YA = F.
Проверка реакций ∑пр. у = 0; YA – YB = 0; 0 = 0.
Разбиваем раму на участки нагружения – стержни AD, CD и СВ. Используя метод сечений, составим выражения для МХ, начиная со стержня АD.
Участок АD (рис. 1.11,в, 0  ≤ Z1 ≤ l ).
≤ Z1 ≤ l ).
|

Участок ВС ( рис. 1.11,г 0 ≤ Z2 ≤ l):
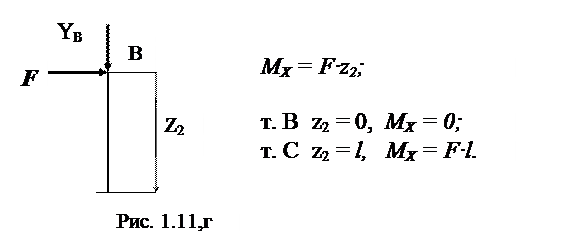
Участок CD (рис. 1.11,д 0 ≤ Z3 ≤ l ):

По полученным выражениям и значениям МХ строим эпюру (рис. 1.12,а). Вычисляем перемещение fгор узла С методом Мора.
 Рис. 1.12
Рис. 1.12
Прикладываем в точке С силу 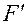 =1 в направлении искомого перемещения (рис. 1.12, б).
=1 в направлении искомого перемещения (рис. 1.12, б).
Находим реакции опор от этой силы.
 х = 0;
х = 0; 
 - 1 = 0; =>
- 1 = 0; => 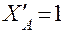 ;
;
 A = 0; -
A = 0; - 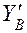 ·l + 1·l = 0; =>
·l + 1·l = 0; => 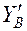 = 1;
= 1;
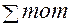 B = 0; -
B = 0; - 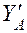 ·l +
·l + 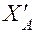 ·2l -
·2l - 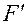 ·l = 0; =>
·l = 0; => 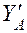 = 1.
= 1.
Проверка реакций: ∑пр. у= 0; 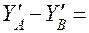 0.
0.
Аналогично изложенному выше строим эпюру изгибающих моментов 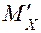 (см. рис. 1.12,б).
(см. рис. 1.12,б).
Из вида эпюр следует, что надо их перемножать на двух участках CD и DA. Искомое перемещение равно:
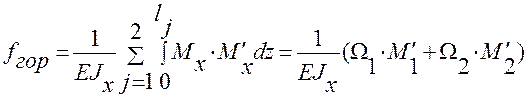 =
=
= 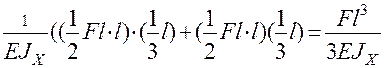 .
.
Перемещение получилось со знаком «плюс», следовательно, узел С переместился в направлении единичной силы 
 = 1, т.е. влево.
= 1, т.е. влево.
Метод сил
Метод сил применяется для раскрытия статической неопреде-лимости систем. В этом методе неизвестными являются обобщенные силы – реакции внешних связей и внутренние усилия от внутренних связей. Процедура метода сил включает понятия основной и эквивалентных систем, составление и решение канонических уравнений.
Порядок раскрытия статической неопределимости систем методом сил.Порядок расчета состоит из следующих шагов:
1) определение степени статической неопределимости;
2) выбор основной системы (О.С.);
3) построение эквивалентной системы (Э.С.);
4) составление системы канонических уравнений;
5) вычисление единичных и грузовых коэффициентов системы канонических уравнений;
6) решение системы канонических уравнений;
7) построение эпюр внутренних силовых факторов для рассчи-тываемой системы;
8) проверка правильности раскрытия статической неопредели-мости.
Основная система
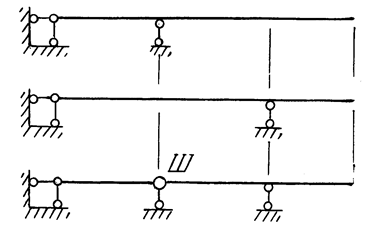
Рис. 1.13
Система, полученная из исходной системы путем снятия внешних нагрузок и освобождения от «лишних» связей, называется основной системой. Эта система должна быть статически определимой и геометрически неизменяемой. Для каждой статически неопределимой системы можно выбрать несколько вариантов основной системы. Например, для статически неопределимой балки, показанной на рис. 1.5,а могут быть предложены три основные системы, представленные на рис. 1.13.
Эквивалентная система
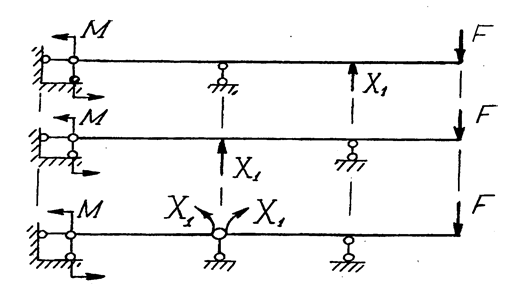
Рис. 1.14
Основная система с приложенными внешними нагрузками и реакциями «лишних» связей называется эквивалентной системой. Неизвестные реакции «лишних» связей обозначаются Х1, Х2 и т.д., где числовой индекс обозначает номер неизвестной.
Для балки (см. рис. 1.5,а), рассмотренной в предыдущих вопросах, соответственно выбранным основным системам (см. рис. 1.13) эквивалентные системы показаны на рис. 1.14.
Канонические уравнения метода силВ общем случае, при n > 1 (где n - количество «лишних» неизвестных) система канонических уравнений метода сил имеет вид:
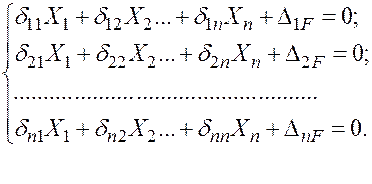
Каждое уравнение этой системы выражает условие равенства нулю перемещения по направлению соответствующей удаленной связи. Направление удаленной связи (i) определяется по первому индексу коэффициентов δij,∆iF. Число уравнений равно степени статической неопределимости (n) системы.
Коэффициенты системы канонических уравнений имеют следующие названия:
δij - единичный коэффициент;
∆ij – грузовой коэффициент.
Каждый из коэффициентов представляет собой перемещение конкретного сечения стержня в определенном направлении. Для их вычисления применяют метод Мора. При этом строят эпюры внутренних силовых факторов при поочередном нагружении основной системы единичными нагрузками (Х´i=1) и заданными нагрузками (F).
Каноническое уравнение метода сил для один раз статически неопределимой системы имеет вид:
δ11Х1+ ∆1F=0.
Пример расчета статической неопределимости балки методом сил
Рассмотрим балку (рис. 1.15,а), для которой раскроем стати-ческую неопределимость и построим эпюры изгибающих моментов Мх и поперечных сил Qy. Примем исходные данные:
F = 2кН; l = 1м; материал упругий; поперечное сечение постоянное по длине балки с жесткостью ЕJx .
Решение.
1. Определяем степень статической неопределимости S заданной системы
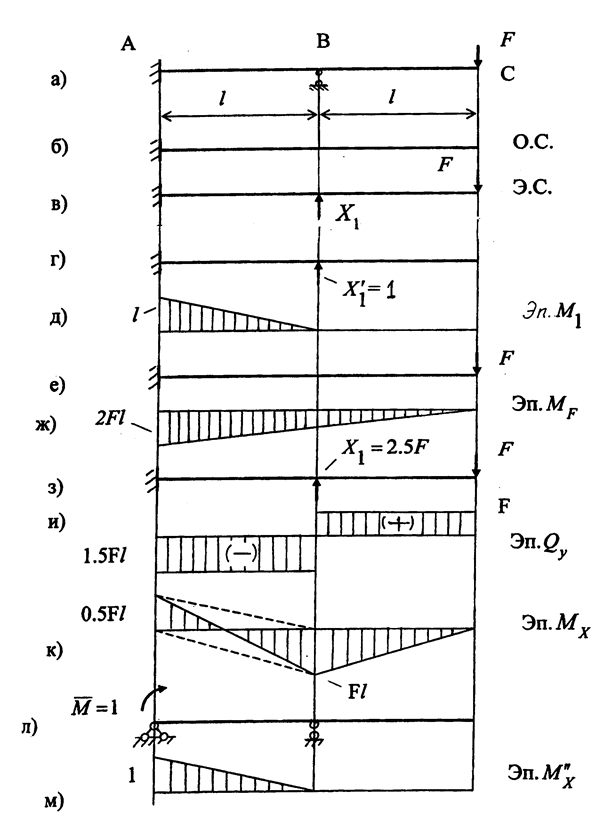
Рис. 1.15
S = n – k = 4 – 3 = 1,
где n – число реакций связей, n = 4;
k – количество уравнений равновесия статики, которые можем записать для данной системы, k = 3. Таким образом, балка один раз статически неопределима.
2. Выбираем основную систему (О.С.) (рис. 1.15,б).
Для получения О.С. заданную систему освобождаем от нагрузки F и одной связи – шарнирно-подвижной опоры В.
3. Строим эквивалентную систему (Э.С.).
Для этого О.С. нагружаем заданной нагрузкой F и неизвестной силой Х1 в поперечном сечении В.
Эквивалентная система показана на рис. 1.15,в.
4. Составляем каноническое уравнение.
Для данной системы, один раз статически неопределимой, каноническое уравнение имеет вид:
δ11Х1+ ∆1F=0.
Нагружаем О.С. поочередно силой Х'1=1 (рис. 1.15,г) и внешней нагрузкой F (рис. 1.15,е).
5. Строим единичную М1 (рис. 1.15,д) и грузовую МF (рис. 1.15,ж) эпюры.
6. Вычисляем единичный и грузовой коэффициенты канонического уравнения.
Перемножая эпюру М1 саму на себя, получим:
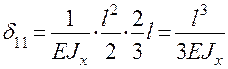 .
.
Перемножая эпюры МF и  , найдем:
, найдем:
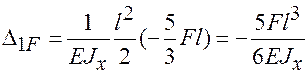 .
.
7. Решаем каноническое уравнение:
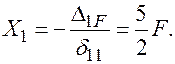
8. Строим эпюры внутренних силовых факторов (Qy и Мх).
Показываем расчетную схему (рис. 1.15,з), для которой строим эпюру поперечных сил Qy (рис. 1.15,и) и эпюру изгибающих моментов Мх (рис. 1.15,к).
9. Проверяем правильность раскрытия статической неопреде-лимости (деформационная проверка).
Берем новую О.С., например, показанную на рис. 1.15,л. Прикладываем единичную нагрузку М'=1 на месте снятой связи. Строим единичную эпюру  .
.
Перемножаем эпюры Мх и М''х
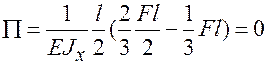 ,
,
где П – обозначение операции проверки.
Полученный результат – ноль означает, что угол поворота в сечении А равен нулю, т.е. построенная эпюра Мх правильна.
Дата: 2016-10-02, просмотров: 293.
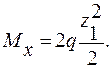 Определяем значения МХ в крайних поперечных сечениях (точках) участка:
т. Е z1 = 0, MX = 0;
т. D z1 = l, MX = ql2.
Определяем значения МХ в крайних поперечных сечениях (точках) участка:
т. Е z1 = 0, MX = 0;
т. D z1 = l, MX = ql2.