СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
ТЕОРИЯ И ЗАДАЧИ
Статически- неопределимые системы, сложное напряженное
состояние, сопротивление усталости
Методические указания к выполнению расчетно-графических заданий, самостоятельной подготовке к зачету и экзамену по курсу «Сопротивление материалов» для студентов заочников
Под редакцией проф., к.т.н. Н.А.Крамского
Москва 2013
Разработано в соответствии с Государственным образовательным стандартом ВПО 2009г. для специальностей
на основе рабочей программы дисциплин «Сопротивление материалов» и «Механика твердого тела»
Рецензенты:
Профессор кафедры «Сопротивление материалов» МГМУ «МАМИ»
к.т.н. Осипов Н.Л.
доцент кафедры «Сопротивление материалов» МГМУ «МАМИ»
к.т.н. Чабунин И.С.
Работа подготовлена на кафедре «Сопротивление материалов»
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ. Теория и задачи. Статически-неопределимые системы, сложное напряженное состояние, сопротивление усталости: методические указания к выполнению РГР, самостоятельной подготовке к зачету и экзамену по курсу «Сопротивление материалов» и «Механика твердого тела» для студентов заочного отделения
Щербаков В.И., Рыбакова М.Р., Стародубец Н.А. – М.:Университет машиностроения «МАМИ», 2013. -116 с.
Методические указания включают краткие теоретические сведения по основным разделам второй части курса сопротивления материалов, а также примеры решения типовых задач расчетно – графических работ, выполняемых студентами заочной формы обучения
© кафедра «Сопротивление материалов» Университет машиностроения, 2013.
©Щербаков В.И.., Рыбакова М.Р., Стародубец Н.А., ред.Крамской Н.А.,2013.
СОДЕРЖАНИЕ
1. Тема 1. Статически – неопределимые системы……………....4
Степень статической неопределимости . Построение эпюр MX, QY, NZ в статически определимых рамах, определение перемещений
Задача 1.1……………………………………………………….….6
Задача 1.2… ………………………………………………….…11
Задача1.3...……………..……………………………………… 14
Метод сил для решения статически неопределимых рам и балок…………………………………………………………………..18
Пример расчета один раз статически неопределимой балки и определение перемещений…………………………………………..20
Задача 1.4…………………………………………………………24
Задача 1.5. Два раза статически неопределимая балка………29
Задача 1.6. Решение один раз статически неопределимой рамы……………………………………………………………….….39
Задача 1.7. Решение симметричной рамы….….…….……....43
Задача 1.8. Решение кососимметричной рамы…………..…...49
2. Тема 2. Анализ напряженного состояния в точке….. ……..51
Эквивалентное напряжение. Теории прочности….…….…....56
Косой изгиб……………..……………………………………….58
3. Тема 3. Расчеты на прочность при сложном напряженном состоянии
Задача 3.1………………………………….……………..……...63
Задача 3.2. Расчет ломаного бруса…………………….….….. 67
Задача 3.3. Определение коэффициента запаса тонкостенной трубки…………………………….…………………………….……75
Задача 3.4. Определение перемещений в ломаном брусе…...80
4. Тема 4. Расчет вала на статическую прочность и сопротивление усталости………………………………………….…………………85
4.4. Пример решения вала с насаженными на него двумя шестернями……………………………………….………………….91
5. Приложение 1……………………..……………….……......107
6. Приложение 2…………………………………………….…114
7. ЛИТЕРАТУРА…………………………….………………..115
Статически определимая стержневая система
Статически определимой называется геометрически неизменяе-мая стержневая система, в которой реакции всех связей (как внеш-них, так и внутренних) при произвольной статической нагрузке могут быть определены из уравнений равновесия всей системы или отдельных ее частей. Примеры таких систем показаны на рис. 1.4.
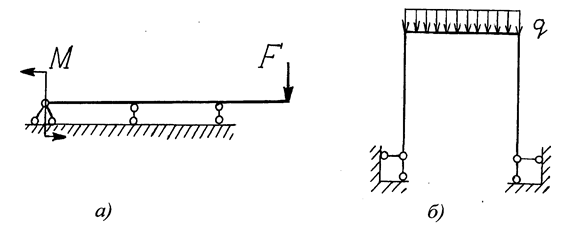
Рис. 1.4
Статически неопределимая стержневая система.
Статически неопределимой называется стержневая система, в которой реакции связей не могут быть определены только при помощи уравнений равновесия. Примеры таких систем показаны на рис. 1.5.
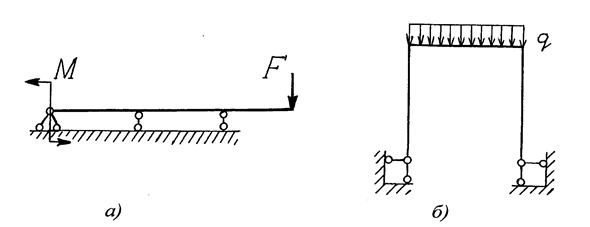Рис. 1.5
Метод сил
Метод сил применяется для раскрытия статической неопреде-лимости систем. В этом методе неизвестными являются обобщенные силы – реакции внешних связей и внутренние усилия от внутренних связей. Процедура метода сил включает понятия основной и эквивалентных систем, составление и решение канонических уравнений.
Порядок раскрытия статической неопределимости систем методом сил.Порядок расчета состоит из следующих шагов:
1) определение степени статической неопределимости;
2) выбор основной системы (О.С.);
3) построение эквивалентной системы (Э.С.);
4) составление системы канонических уравнений;
5) вычисление единичных и грузовых коэффициентов системы канонических уравнений;
6) решение системы канонических уравнений;
7) построение эпюр внутренних силовых факторов для рассчи-тываемой системы;
8) проверка правильности раскрытия статической неопредели-мости.
Основная система
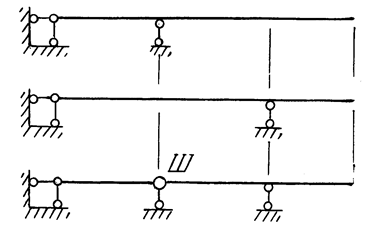
Рис. 1.13
Система, полученная из исходной системы путем снятия внешних нагрузок и освобождения от «лишних» связей, называется основной системой. Эта система должна быть статически определимой и геометрически неизменяемой. Для каждой статически неопределимой системы можно выбрать несколько вариантов основной системы. Например, для статически неопределимой балки, показанной на рис. 1.5,а могут быть предложены три основные системы, представленные на рис. 1.13.
Эквивалентная система
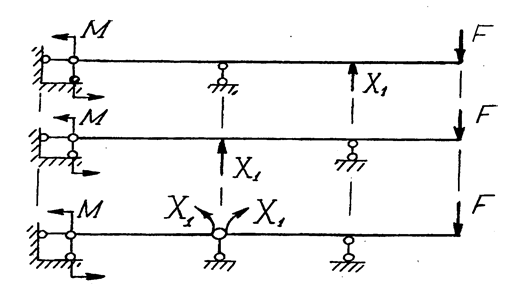
Рис. 1.14
Основная система с приложенными внешними нагрузками и реакциями «лишних» связей называется эквивалентной системой. Неизвестные реакции «лишних» связей обозначаются Х1, Х2 и т.д., где числовой индекс обозначает номер неизвестной.
Для балки (см. рис. 1.5,а), рассмотренной в предыдущих вопросах, соответственно выбранным основным системам (см. рис. 1.13) эквивалентные системы показаны на рис. 1.14.
Канонические уравнения метода силВ общем случае, при n > 1 (где n - количество «лишних» неизвестных) система канонических уравнений метода сил имеет вид:
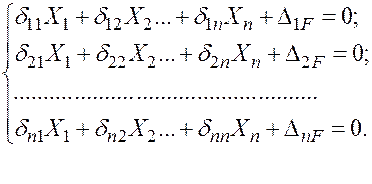
Каждое уравнение этой системы выражает условие равенства нулю перемещения по направлению соответствующей удаленной связи. Направление удаленной связи (i) определяется по первому индексу коэффициентов δij,∆iF. Число уравнений равно степени статической неопределимости (n) системы.
Коэффициенты системы канонических уравнений имеют следующие названия:
δij - единичный коэффициент;
∆ij – грузовой коэффициент.
Каждый из коэффициентов представляет собой перемещение конкретного сечения стержня в определенном направлении. Для их вычисления применяют метод Мора. При этом строят эпюры внутренних силовых факторов при поочередном нагружении основной системы единичными нагрузками (Х´i=1) и заданными нагрузками (F).
Каноническое уравнение метода сил для один раз статически неопределимой системы имеет вид:
δ11Х1+ ∆1F=0.
Пример расчета статической неопределимости балки методом сил
Рассмотрим балку (рис. 1.15,а), для которой раскроем стати-ческую неопределимость и построим эпюры изгибающих моментов Мх и поперечных сил Qy. Примем исходные данные:
F = 2кН; l = 1м; материал упругий; поперечное сечение постоянное по длине балки с жесткостью ЕJx .
Решение.
1. Определяем степень статической неопределимости S заданной системы
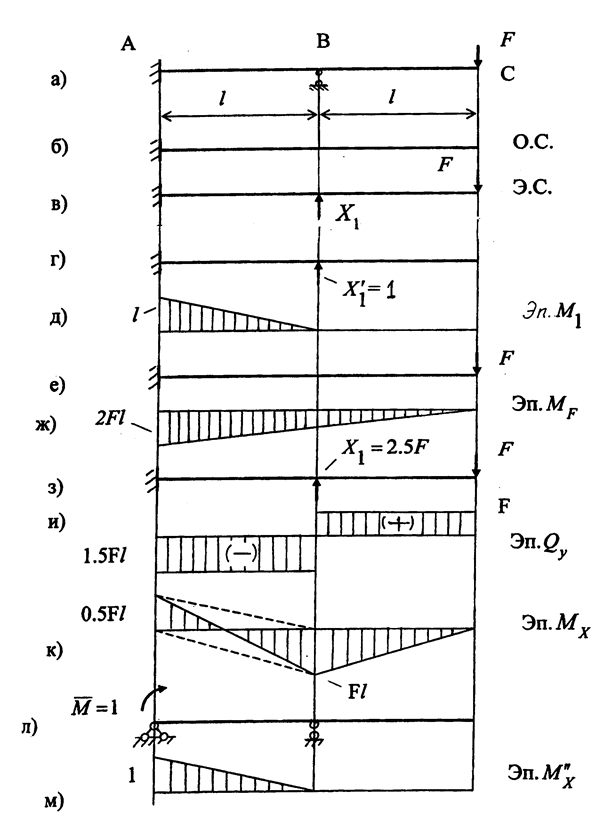
Рис. 1.15
S = n – k = 4 – 3 = 1,
где n – число реакций связей, n = 4;
k – количество уравнений равновесия статики, которые можем записать для данной системы, k = 3. Таким образом, балка один раз статически неопределима.
2. Выбираем основную систему (О.С.) (рис. 1.15,б).
Для получения О.С. заданную систему освобождаем от нагрузки F и одной связи – шарнирно-подвижной опоры В.
3. Строим эквивалентную систему (Э.С.).
Для этого О.С. нагружаем заданной нагрузкой F и неизвестной силой Х1 в поперечном сечении В.
Эквивалентная система показана на рис. 1.15,в.
4. Составляем каноническое уравнение.
Для данной системы, один раз статически неопределимой, каноническое уравнение имеет вид:
δ11Х1+ ∆1F=0.
Нагружаем О.С. поочередно силой Х'1=1 (рис. 1.15,г) и внешней нагрузкой F (рис. 1.15,е).
5. Строим единичную М1 (рис. 1.15,д) и грузовую МF (рис. 1.15,ж) эпюры.
6. Вычисляем единичный и грузовой коэффициенты канонического уравнения.
Перемножая эпюру М1 саму на себя, получим:
.
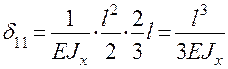Перемножая эпюры МF и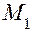 
, найдем:
.
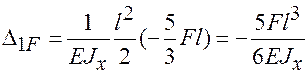7. Решаем каноническое уравнение:
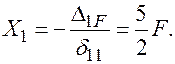
8. Строим эпюры внутренних силовых факторов (Qy и Мх).
Показываем расчетную схему (рис. 1.15,з), для которой строим эпюру поперечных сил Qy (рис. 1.15,и) и эпюру изгибающих моментов Мх (рис. 1.15,к).
9. Проверяем правильность раскрытия статической неопреде-лимости (деформационная проверка).
Берем новую О.С., например, показанную на рис. 1.15,л. Прикладываем единичную нагрузку М'=1 на месте снятой связи. Строим единичную эпюру 
.
Перемножаем эпюры Мх и М''х
,
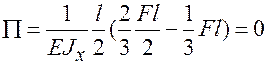где П – обозначение операции проверки.
Полученный результат – ноль означает, что угол поворота в сечении А равен нулю, т.е. построенная эпюра Мх правильна.
ЗАДАЧА 1.6.
Для показанной на рис. 1.29 рамы (З.С.) построить эпюры изгибающих моментов МХ и поперечных QY сил. Определить для узла С горизонтальное перемещение fгор.
|
|
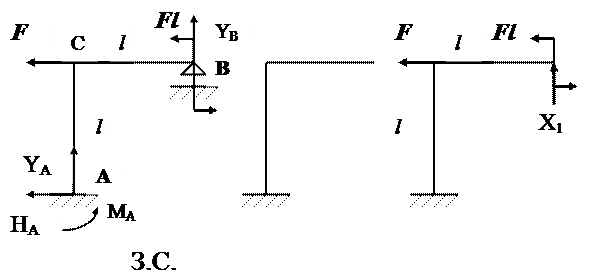
Рис. 1. 29
Решение
Определяем степень статической неопределимости рамы. В опорах возникают четыре опорные реакции. Тогда степень стати-ческой неопределимости S равна:
S = 4 – 3 = 1.
Решаем задачу методом сил. Выбираем основную систему (О.С.), отбрасывая опору В и снимая все нагрузки.
Загружаем (О.С.) заданными нагрузками и «лишней» неизве-стной Х1 , приложенной вместо опоры В. Получаем эквивалентную систему (Э.С.).
Каноническое уравнение имеет вид:
.
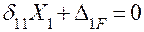Для определения коэффициентов уравнения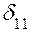 
и 
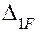строим эпюры изгибающих моментов от Х1 = 1 (Эп. М1) и заданных нагрузок (Эп. MF) рис. 1.30.
Построение эпюры изгибающих моментов от заданных сил.
Участок ВС (0 ≤ Z1 ≤ l ):
МХ = Fl .
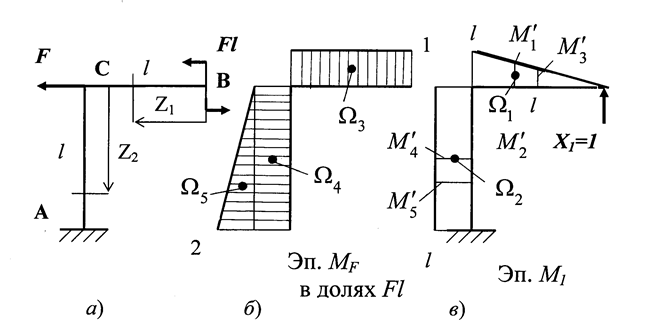
Рис. 1. 30
Участок СА ( 0 ≤ Z2 ≤ l):
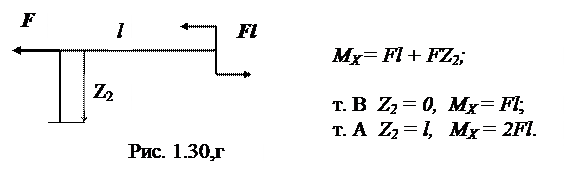
По найденным значениям MX строим эпюру изгибающих мо-ментов (Эп. MF).
Перемножаем эпюру от М1 саму на себя и находим коэффициент :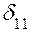
= 
.
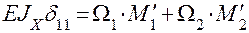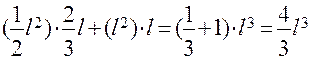Перемножаем эпюру от заданных нагрузок (Эп. MF) на эпюру от единичной силы (Эп. M1) и находим коэффициент :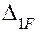
= 
.
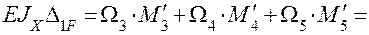
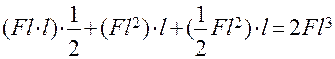Определяем значение «лишней» неизвестной Х1:
.
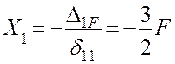Рис. 1. 31
Прикладываем в эквивалентной системе силу Х1 с учетом знака и строим эпюры изгибающих моментов МХ и поперечных сил QY.
Участок СВ (0 ≤ Z1 ≤ l):
MX = Fl – 1,5F·Z1;
т. В Z1 = 0, MX = Fl; т.С Z2 = l, MX = -0,5Fl.
Участок СА (0 ≤ Z2 ≤ l):
MX = Fl – 1,5Fl + F·Z2;
т. С Z2 = 0, MX = - 0,5Fl; т. A Z2 = l, MX = 0,5Fl.
Соответствующие эпюры МХ и QY показаны на рис. 1.31.
Проверка решения. Перемножаем построенную эпюру МХ на единичную эпюру (Эп. М1), показанные на рис. 1.32 .
Рис. 1.32
EJX П = 
=
= 
.
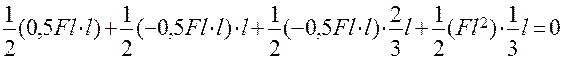Определение перемещения узла С в горизонтальном направлении - fгор. К основной системе в узле С рамы в заданном направлении приложим силу F1 = 1.
Построим эпюру изгибающих моментов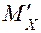 
. Методом Мора, используя правило Верещагина, вычисляем перемещение fгор .
= 
=
= 
.
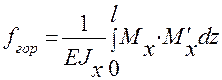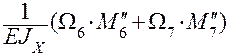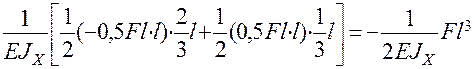Знак минус в полученном выражении означает, что перемещение узла С рамы происходит в противоположном направлении к принятому направлению 
= 1.
ЗАДАЧА 1.7.
Для, показанной на рис. 1.33 рамы построить эпюры изгибающих моментов и поперечных сил, а также подобрать размеры прямоугольного сечения с размерами h и b (h=2b).
Дано: F = 1,5ql, q =25кН/м, l=0,6м.
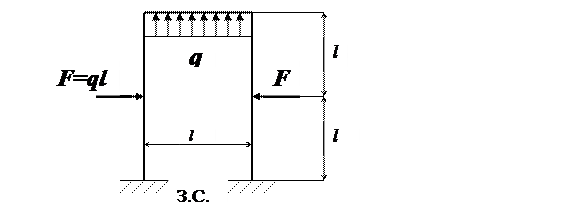
Рис. 1.33
Решение
Рама имеет две опоры – жесткие заделки. В каждой из них возникают три реакции – момент, горизонтальная и вертикальная силы. Таким образом получаем шесть реакций. Вычитая три урав-нения статики, устанавливаем, что рама три раза статически неоп-ределима S = 3.
Однако рама, вместе с приложенными нагрузками, обладает симметрией относительно вертикальной оси. В этом случае если разрезать раму при выборе основной системы по оси симметрии, то вместе разреза будут возникать только две «лишние» неизвестные Х1 и Х2, а кососимметричные неизвестные Х3 равны нулю. Таким образом получаем, что данная рама с приложенными к ней нагрузками два раза статически неопределима. На рис. 1.34 показана основная система (О.С.) – рама разрезана по оси симметрии и эквивалентная система (Э.С.), когда к основной системе приложены лишние неизвестные Х1, Х2 и заданные нагрузки - сосредоточенная сила F и распределенная нагрузка q.
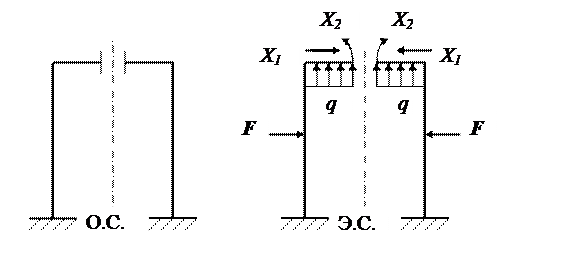
Рис. 1.34
Записываем систему канонических уравнений метода сил:
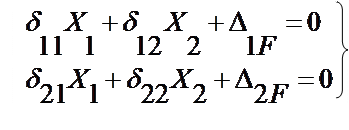
Для определения коэффициентов канонических уравнений строим эпюры изгибающих моментов от Х1 =1, Х2 =1 и заданных нагрузок, которые обозначены М1, М2, МF и показаны на рис. 1.35.
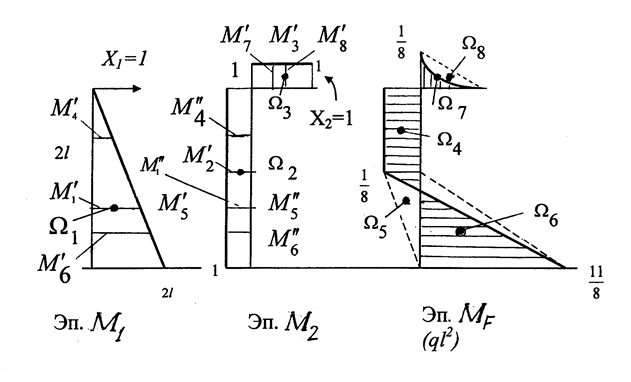Рис. 1.35
Перемножаем эпюру М1 самое на себя:
;
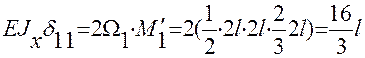Перемножаем эпюру М1 на эпюру М2:
;
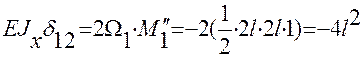Перемножаем эпюру М2 самое на себя:
;
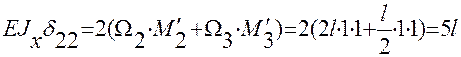Перемножаем эпюру М1 на эпюру МF:
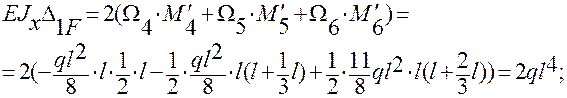
Перемножаем эпюру М2 на эпюру МF:
=
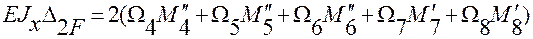=2(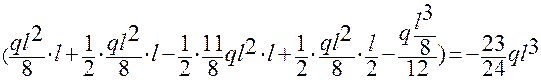 
.
Подставляем полученные значения коэффициентов в кано-нические уравнения, решаем систему и находим значения «лишних» неизвестных Х1 и Х2.
; 
.
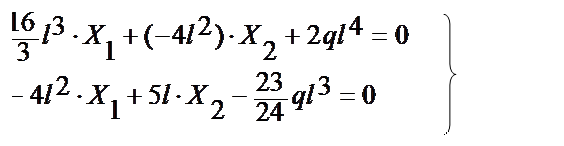
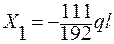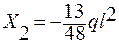Прикладываем Х1 и Х2 с учетом знаков к эквивалентной системе и строим эпюры изгибающих моментов и поперечных сил (рис. 1.36).
Рис. 1.36
Участок АВ ( 0 ≤ z1 ≤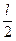 
):
;
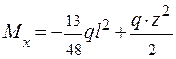т. A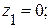 
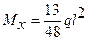; т. В 
; 
.
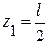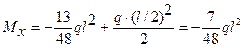Qy = -q·z1;
т. А z1 = 0; Qy = 0; т. В z1 = l/2; Qy =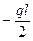 
.
Участок ВС 
( 0 ≤ z2 ≤ l ):
;
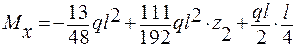т. В z2 = 0; 
;
т. С z2 = l; 
.
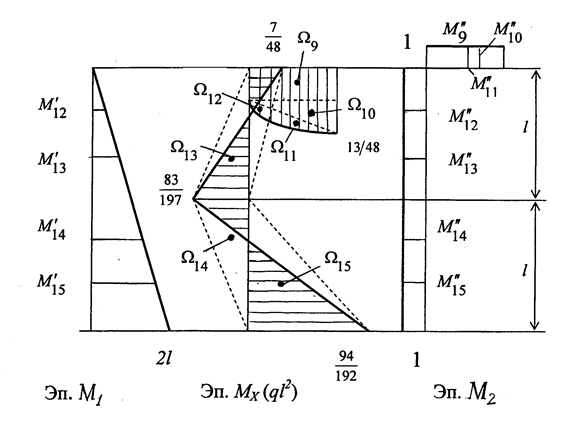
Рис. 1.37
Участок СД ( l ≤ z3 ≤ 2l ):
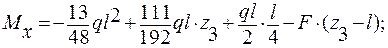
т. С z3 = l;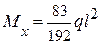 
;
т. D z3 = 2l;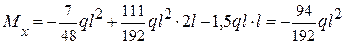 
.
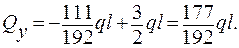
Выполним проверку правильности решения задачи. Перемножим полученную эпюру изгибающих моментов МХ на эпюры от М1 и М2.
=
= 
+ 
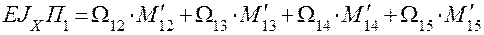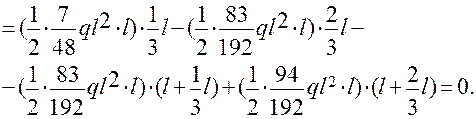
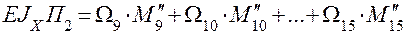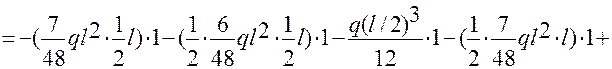
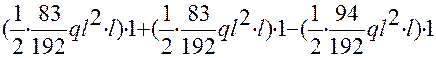= 0.
Задача решена верно.
Определим размеры прямоугольного сечения рамы.
.
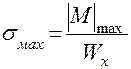Приравнивая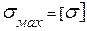 
= 100МПа; 
= 
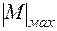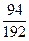ql2; q =25кН/м; l =0,6м, и зная WX = (b·h2)/12 и h = 2b,
получим: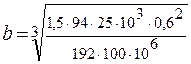 
. b=4·10-2 м, h = 8·10-2м.
ЗАДАЧА 1.8.
Построить эпюру изгибающих моментов для рамы, показанной на рис. 1.38.
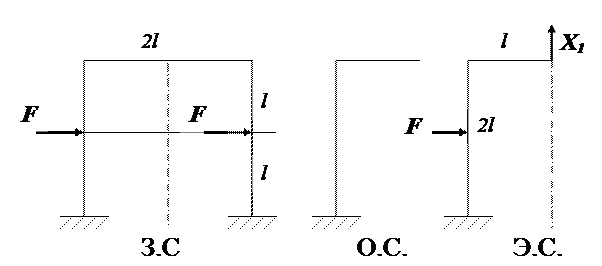
Рис. 1.38
Данная рама имеет геометрическую ось симметрии и нагружена– кососимметричными силами F. Поэтому при ее разрезании, по оси симметрии, как показано на рисунке, все симметричные силовые факторы равны нулю. Таким образом, задача один раз статически неопределима.
Каноническое уравнение метода сил:
.
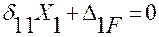Для вычисления коэффициентов этого уравнения строим эпюры изгибающих моментов от «лишней» неизвестной Х1 = 1 и внешних сил - силы F . Эпюры М1 и МF даны на рис. 1.39.
Вычисляем значения коэффициентов этого уравнения.
Перемножаем эпюру М1 самое на себя:
.
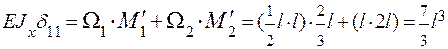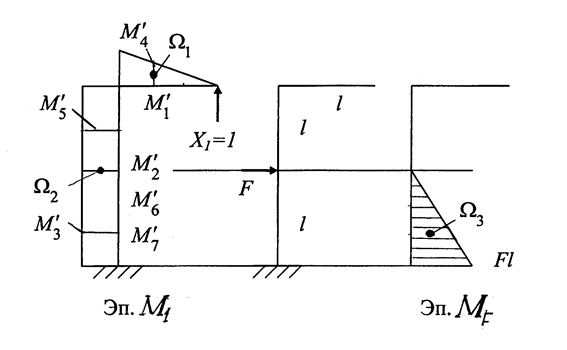
Рис. 1.39
Перемножаем эпюру МF на эпюру М1:
.
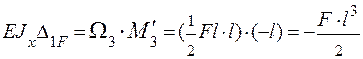Тогда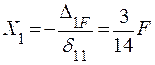 
.
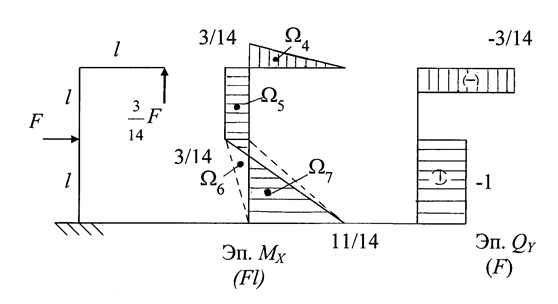
Рис. 1.40
Строим эпюры изгибающих моментов МХ и поперечных сил QY от заданной силы F и подсчитанной «лишней» неизвестной Х1 (рис. 1.40).
Проверка правильности решения задачи. Перемножаем эпюру МХ на эпюру М1.
EJX П1 =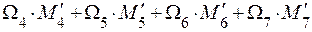 
=
= 
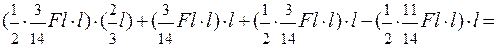0.
Задача решена верно.
Объемная деформация
Наряду с линейной и угловой деформациями рассматривают и объемную е , т.е. относительное изменение объема в точке:
е =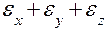 
= 
.
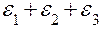Относительное изменение объема равно сумме линейных де-формаций по трем взаимно перпендикулярным осям.
С поворотом осей величина е не меняется.
Обобщенный закон Гука
Обобщенный закон Гука для объемного напряженного состояния записывается (в главных напряжениях):
= 
,
= 
= 
.
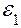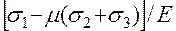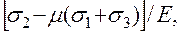
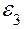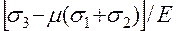Относительное изменение объема равно:
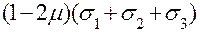е = 
/Е.
Из этой формулы следует, что изменение объема не происходит (е = 0) в двух случаях:
если 1 - 2µ = 0, т.е. при µ = 0,5;
если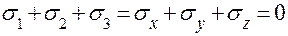 
.
При растяжении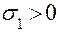 
; 
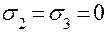. Поэтому растяжение сопровождается увеличением объема е > 0.
При сжатии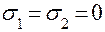 
, 
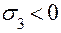получим е < 0. Следовательно, при сжатии стержня его объем уменьшается.
Чистый сдвиг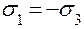 
; 
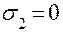. Таким образом имеем, что при чистом сдвиге объем тела не меняется.
Эквивалентное напряжение
Напряженное состояние в точке может быть задано главными напряжениями. В общем случае все они не равны нулю. Для расчета на прочность оно заменяется эквивалентным (равнопрочным, т.е. имеющим такой же запас прочности) одноосным растяжением, которое и рассчитывается на прочность (рис.2.4).
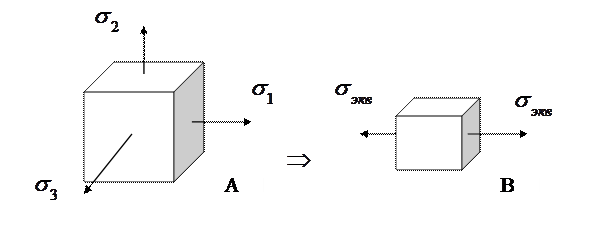
Состояние А равноопасно состоянию В
Рис. 2.4
Теории прочности
Переход от сложного напряженного состояния к эквивалент- ному осуществляется по теориям (гипотезам) прочности.
В сопротивлении материалов изучаются следующие теории прочности:
1) теория наибольших нормальных напряжений
= 
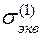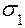; (2.4)
2) теория наибольших линейных деформаций
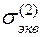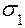= - µ (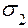 
+ 
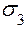) ; (2.5)
3) теория наибольших касательных напряжений
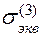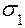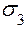= - ; (2.6)
4) теория удельной потенциальной энергии деформации изменения формы
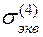= (1/ 
)
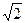;(2.7)
5) теория Мора
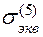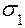= -k 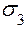, где k = 
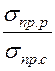. (2.8)
Здесь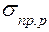 
, 
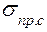предельные напряжения на растяжение и сжатие. В машиностроительных конструкциях часто встречаются детали, работающие на изгиб и кручение одновременно. В этом случае выделенный из детали элемент, находится под действием нормальных и касательных напряжений (рис. 2.5).
Рис. 2.5
При расчете пластичных материалов, одинаково сопротивля-ющихся растяжению и сжатию (обычные стали), в основном используют третью и четвертую теории прочности, а материалов с различными свойствами на растяжение и сжатие (закаленная сталь, чугун и др.) – теорию прочности Мора.
Для такого частного случая двухосного напряженного состояния, принимая в формуле (2.2)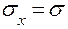 
, 
, 
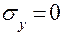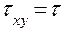, получают расчетные формулы (2.6) –(2.8) в следующем виде:
Теория 3 =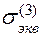 
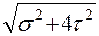; (2.9)
Теория 4 . =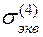 
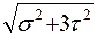; (2.10)
Теория 5 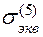= 0.5 (1-k) 
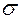+ 0.5 (1+k) 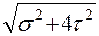. (2.11)
Косой изгиб
Косым изгибом называется такой вид нагружения бруса, при котором плоскость действия нагружающего момента М не совпа-дает ни с одной из главных центральных осей инерции поперечного сечения (рис. 2.6).
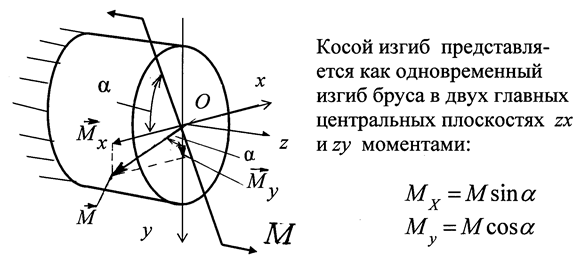
Рис. 2.6
Ядро сечения
Ядром сечения называется область в окрестности центра тяжести сечения, обладающая следующим свойством. Если приложить силу F внутри или на границе ядра сечения, то во всем сечении напряжения будут одного знака.
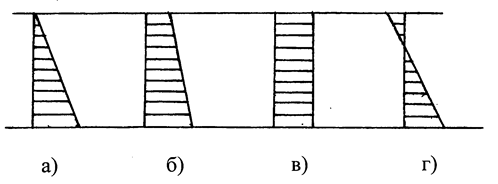
Рис. 2.11
На рис. 2.11 показаны эпюры нормальных напряжений в сечении бруса, если сила приложена а) - на контуре ядра сечения, б) - внутри, г) вне ядра сечения и в) - в центре тяжести сечения бруса.
ЗАДАЧА 3.1.
Элемент, показанный на рис. 3.1,а, находится под действием напряжений 
, 
, 
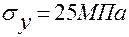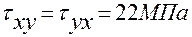. Требуется найти величину главных напряжений и положение площадок, по которым они действуют.
Решение.
Для рассматриваемого элемента одна из главных площадок (плоскость хоу) известна. Требуется определить положение двух других главных площадок и значения главных нормальных напряжений, действующих на этих площадках. При подстановке значений напряжений в формулы нам потребуются следующие правила знаков. Растягивающее нормальное напряжение 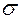считается положительным, сжимающее – отрицательным. Касательное напряжение 
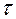положительно, если оно стремится повернуть элемент по часовой стрелке относительно оси, индекса которой нет в его обозначении (в нашем случае относительно оси z).
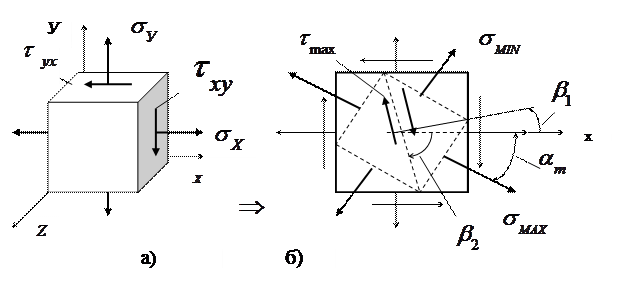
Рис. 3.1
Положение главной площадки к оси х определяется углом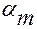 
, значение которого вычисляем по формуле (2.3):
.
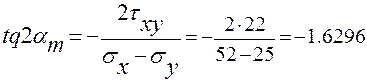Откуда
.
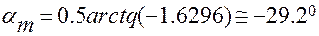При 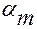> 0 элемент с главными площадками повернут отно-сительно исходного элемента против хода часовой стрелки,
при 
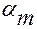< 0 – в противоположном направлении.
В нашем случае элемент с главными площадками изображен пунктиром на рис. 3.1,б.
Значения главных напряжений, действующих по найденным гла-вным площадкам, определяются по формуле (2.2):
.
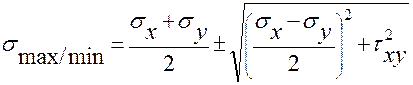Вычисления по этой формуле приводят к следующим результа-там:
,
.
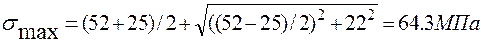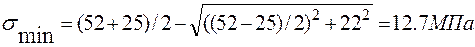Эти же главные напряжения можно также получить, используя формулу для определения нормальных напряжений в площадках наклоненных к оси х под углом α
,
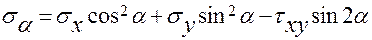в которую следует поочередно подставить кроме заданных напря-жени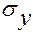й 
, 
и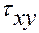 
значения углов:
; 
.
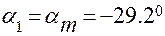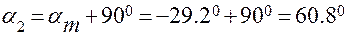При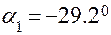 
имеем:
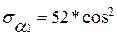
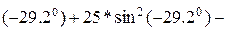22*sin 
.
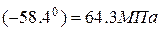При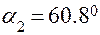 
имеем:
.
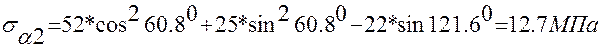Учитывая принятое соотношение между главными напряжениями
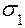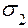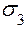≥ ≥ , получаем:
; 
; 
.
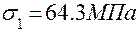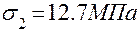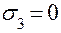Далее следует показать найденные напряжения на элементе (см. рис. 3.1,б). При первом варианте определения главных напряжений надо большее из найденных напряжений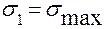 
показывать на главных площадках, ориентированных к тем угловым точкам исходного элемента, к которым сходятся касательные напряжения. В случае использования второго варианта расчета трудностей с рас-становкой главных напряжений нет.
Инвариантность суммы нормальных напряжений, действующих во взаимно перпендикулярных площадках двух разных по углу поворота элементов, проверяется по формуле:
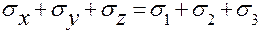= const.
В нашей задаче
52+ 25 +0 = 64.3 +12.7 + 0 = 77,
что подтверждает правильность вычислений.
Значение максимального касательного напряжения в плоскости, параллельной плоскости хоу, вычислим по формуле:
.
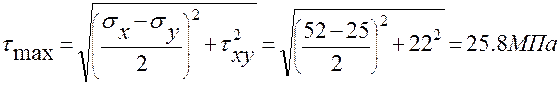Это же значение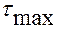 
можно получить через главные напряжения, лежащие в плоскости, параллельной плоскости хоу. В рассматриваемом примере такими являются
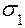= 64.3 МПа и 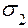=12.7 МПа.
Тогда найдем
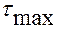= (64.3 – 12.7)/2 = 25.8МПа.
Площадки, по которым действуют эти напряжения, наклонены к главным площадкам на угол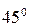 
. Нормали к площадкам с 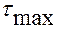составят с осью х угол:
;
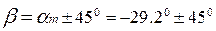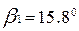(повернуть против хода часовой стрелки);
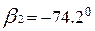(повернуть по ходу часовой стрелки).
При необходимости определения максимальных касательных напряжений без ограничения плоскости их расположения они нахо-дятся по формуле:
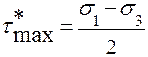
справедливой для любого вида напряженного состояния. В нашем примере
.
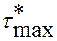
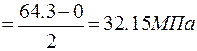Это напряжение действует в площадке, равно наклоненной к площадкам 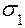(максимального) и 
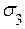(минимального) из главных напряжений.
ЗАДАЧА 3.2.
Ломаный брус (рис. 3.2) загружен силами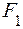 
= 2кН, 
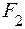= 1кН, равномерно распределенной нагрузкой интенсивностью q = 1 кН/м и моментом Т =1 кНм. Размеры бруса a = 1 м, с = 1 м.
Требуется подобрать:
на участке АВ – размер диаметра круглого сплошного сечения;
на участке ВС - размеры h и b ( h = 2 b ) прямоугольного се-чения. Материал бруса - сталь 
, 
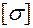= 160 МПа.
При расчетах использовать теорию прочности максимальных касательных напряжений.
Построение эпюр изгибающих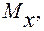 
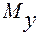и крутящего 
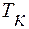моментов. В сечениях бруса под действием приложенных внешних сил и моментов возникают изгибающие и крутящий моменты, поперечные и нормальная силы. При расчете на проч-ность таких брусьев влиянием поперечных и нормальных сил обычно пренебрегают. Поэтому для рассматриваемого примера эпюры поперечных и нормальных сил не строим.
Приступая к решению задачи, прежде всего, необходимо на каждом участке бруса (см. рис. 3.2,а) показать скользящую систему координат xyz в сечениях А и В (ось z должна быть направлена вдоль оси бруса).
Далее, делая обход со свободного конца бруса по его контуру (переходя от одного участка к следующему участку бруса, наблюдатель не должен пересекать ось z ), записываем выражения изгибающих и крутящих моментов для текущих сечений каждого участка бруса.
Участок АМ:
(плоскость zy)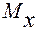 
= 0; (плоскость zx) 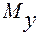= q 
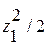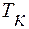; = Т.
Участок МВ:
= 
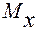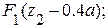
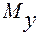=q(0.4a)( 
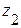-0.2a); 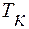= Т.
Участок ВЕ:
= 
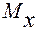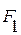(0,6a); 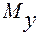= T + q( 0,4 a) 
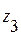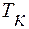; = - q(0,4a)(0,8a).
Участок ЕС:
=
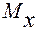Дата: 2016-10-02, просмотров: 168.
