Используют метод Мора. Для этого кроме построенной после раскрытия статической неопределимости эпюры Мх следует рассмотреть соответствующее единичное состояние системы, приложив единичную нагрузку (силу F'=1 или момент М'=1) в любой основной системе, и построить эпюру изгибающих моментов (М'х или М''х). Искомое перемещение вычисляется путем «перемножения» эпюр Мх и М'х для линейного перемещения или Мх и М''х - углового перемещения.
Так, если требуется найти прогиб концевого поперечного сечения С балки (см. рис. 1.15,а), для которой была раскрыта статическая неопределимость и построена эпюра Мх (см. рис. 1.15, к), следует приложить единичную силу F'=1 в сечении С основной системы (рис. 1.16,а), построить эпюру изгибающих моментов М'х (рис. 1.16,б) и перемножить ее с вышеупомянутой эпюрой Мх по правилу Верещагина
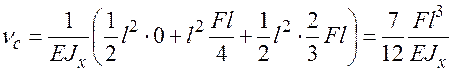 .
.
Найденное перемещение (прогиб) направлено вниз.
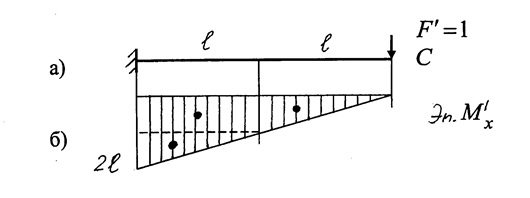
Рис. 1.16
 ЗАДАЧА 1.4.Для балки, показанной на рис. 1.17 (З.С.), по-строить эпюру изгибающих моментов МХ и поперечных сил QY.
ЗАДАЧА 1.4.Для балки, показанной на рис. 1.17 (З.С.), по-строить эпюру изгибающих моментов МХ и поперечных сил QY.
Решение
Показываем реакции опор и определяем степень статической неопределимости балки (рис. 1.17 ). Число реакций 3, уравнений статики 2, тогда степень статической неопределимости:
S = 3 – 2 = 1.
Таким образом балка один раз статически неопределима. Решаем данную балку методом сил.
Выбираем основную систему О.С.– статически определимую балку без нагрузок, отбрасывая опору С.
Эквивалентная система Э.С. Загружаем О.С. заданными нагрузками и «лишней» неизвестной Х1 (отброшенная реакция опоры С).
Записываем одно каноническое уравнение метода сил:
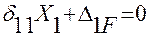 .
.
Для определения коэффициентов этого уравнения строим эпюры изгибающих моментов от Х1 =1 (Эп. М1) и внешних сил (Эп. MF). Построение эпюр внутренних силовых факторовот внешних нагрузок дано на рис. 1.18.
Показываем направления и находим значения реакций опор YA и YB.
∑mom A = 0; - 2ql·0,5l + YB·l + 0,5ql2 = 0; YB = 0,5ql.
∑mom B = 0; - YA·l + 2ql·0,5l + 0,5ql2 = 0; YA = 1,5ql.
Проверка реакций:
∑пр. у = 0; YA + YB – 2ql = 0. 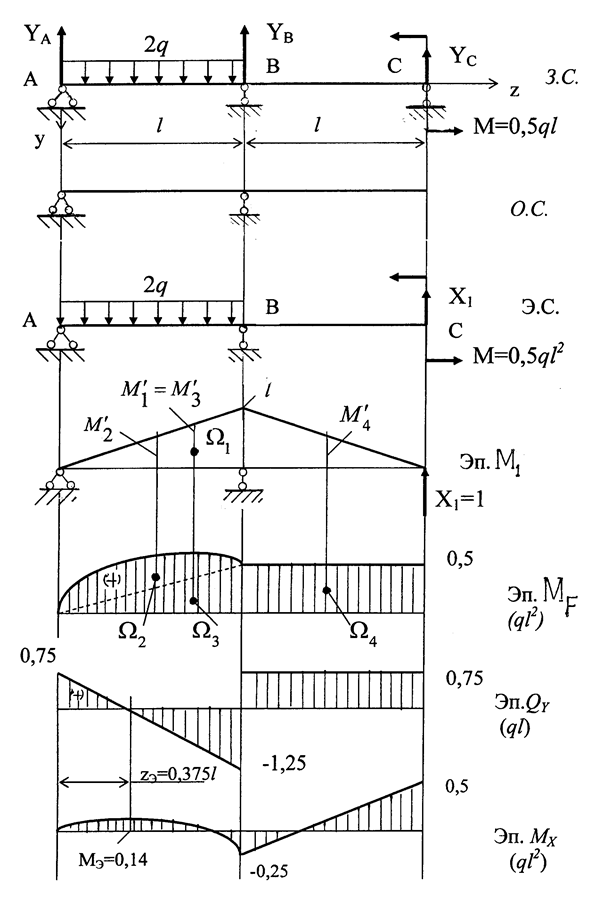
Рис. 1.17
Балка имеет два участка нагружения АВ и ВС. На каждом участке записываем выражения изгибающих моментов МХ и поперечных сил QY, по которым строим их эпюры. 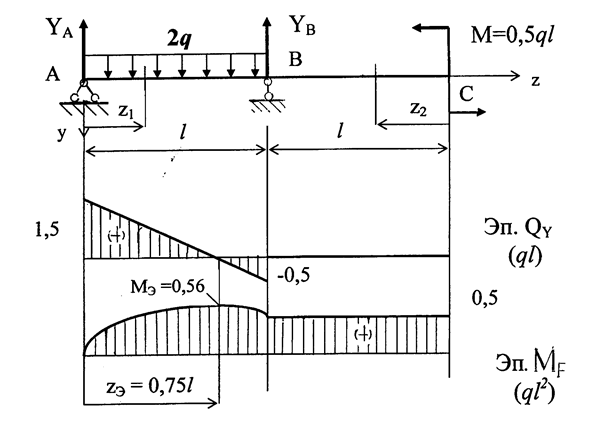
Рис. 1.18
Участок АВ ( 0 ≤ z1 ≤ l ):
QY = YA – 2qz1;
точка А, z1 = 0: QY = YA = 1,5ql;
т. В, z1 = l: QY = YA – 2ql = -0,5ql.
MX = YA·z1 – 2q 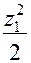
т. A, z1 = 0: MX = 0;
т. B, z1 = l: MX = 1,5ql·l – 2q 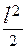 = 0,5ql2.
= 0,5ql2.
Находим точку перегиба на эпюре МХ. Для этого приравниваем QY =0:
QY = YA – 2q·zЭКС = 0 ; => ZЭКС = 0,75l;
MЭКС = YA·ZЭКС – 2q 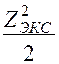 = 0,56ql2.
= 0,56ql2.
Вычисляем значения коэффициентов канонического уравнения 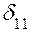 и
и 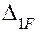 (рис. 1.17):
(рис. 1.17):
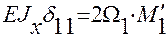 = 2(0,5·l·l)·(0,75l) =
= 2(0,5·l·l)·(0,75l) = 
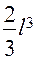 ;
;
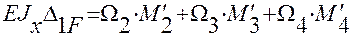 =
=
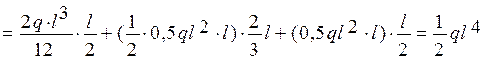 .
.
Значение Х1 равно: 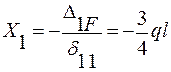 , которое прикладываем в эквивалентной системе с учетом знака (рис. 1.19).
, которое прикладываем в эквивалентной системе с учетом знака (рис. 1.19). 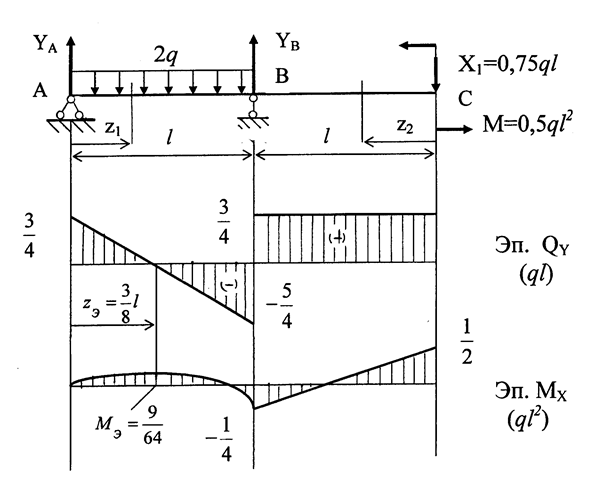
Рис. 1.19
Строим эпюры изгибающих моментов МХ и поперечных сил QY.
Находим реакции опор.
∑mom A =0; -2ql· 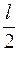 + YB·l + 0,5ql2 -
+ YB·l + 0,5ql2 -  ql·2l = 0;
ql·2l = 0;
YB = 2ql.
∑mom B =0: -YA·l + 2ql· 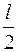 + 0,5ql2 -
+ 0,5ql2 -  ql·l = 0;
ql·l = 0;
YA = 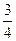 ql.
ql.
Проверка реакций:
∑пр. у = 0; YA + YB – 2ql -  ql = 0 .
ql = 0 .
Строим эпюры МХ и QY по участкам нагружения.
Участок АВ ( 0 ≤ z1 ≤ l ):
QY = YA -2q·z1;
т. А z1 = 0, QY = YA =  ql;
ql;
т. В; z1 = l, QY = 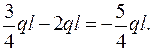
MX = YA·z1 – 2q· 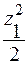 ;
;
т. А z1 = 0, MX = 0;
т. В z1 = l, MX = 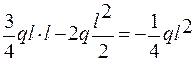 .
.
Находим точку перегиба.
QY = 0; YA – 2q·zэкс = 0; => zЭКС = 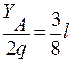 ;
;
MЭКС = YA·zЭКС - 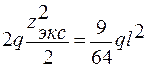 .
.
Участок ВС ( 0 ≤ z2 ≤ l ):
QY = 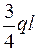 ;
;
MX = 0,5ql2 - 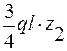 ;
; 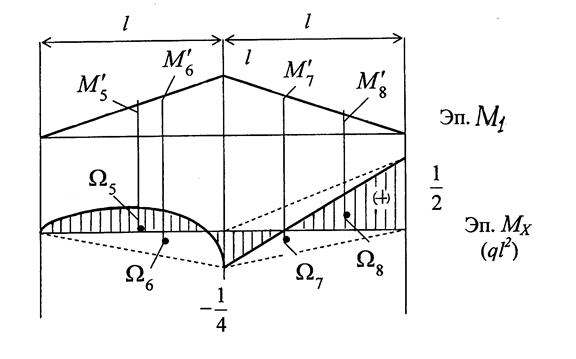
Рис. 1.20
т. С; z2 = 0; MX = 0,5ql2; т.В; z2=l; MX =-0,25ql2.
Проверка правильности решения.
Перемножаем эпюру МХ на эпюру М1 способом Верещагина:
EJXП = 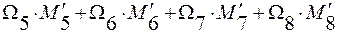 =
= 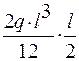 +
+
+ 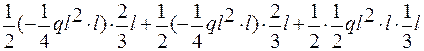 = 0.
= 0.
Задача решена верно.
ЗАДАЧА 1.5.Для многоопорной (неразрезной) балки, пока-занной на рис. 1.21, построить эпюры изгибающих моментов и поперечных сил, подобрать поперечное сечение - двутавр, если [ 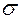 ] = 160 МПа.
] = 160 МПа.
Дано: М = ql2, F = 1,5ql, q =25кН/м, l=0,6м.
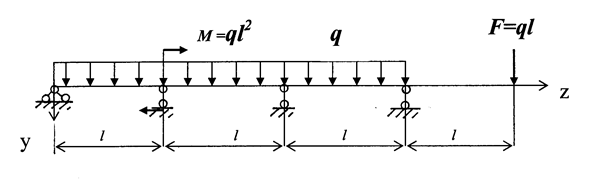
Рис. 1.21
Решение
Определяем степень статической неопределимости балки. Показываем реакции опор. На левом конце балки опора шарнирно- неподвижная. В ней возникают две реакции – вертикальная и горизонтальная. Остальные опоры шарнирно подвижные. Так как горизонтальных сил на балку не действует, то, следовательно, горизонтальной реакции не возникает. Таким образом, в опорах действуют только четыре вертикальные реакции. Для их определения можно использовать только два уравнения статики, например, (суммы моментов). Тогда степень статической неопределимости
S = 4 – 2 = 2.
Поэтому балка два раза статически неопределима.
Решаем задачу методом сил. На рис. 1.22 показаны: З.С. - заданная система. О.С. – основная система, полученная из заданной врезанием в надопорные сечения балки шарниров. Особенностью выбора основных систем при раскрытии статической неопределимости многопролетных балок является то, что вместо удаления лишних внешних связей (опор) рекомендуется отбрасывать простые внутренние связи (связи между поперечными сечениями балки). Для этого в надопорные сечения балки врезаются шарниры, каждый из которых понижает степень статической неопределимости задачи на единицу. В этом случае «лишними» «лишними» неизвестными будут моменты на опорах Х1 и Х2, приложеннымив надопорных сечениях В и С.
Эквивалентная система Э.С. – отдельные балки АВ, ВС и СДЕ, загруженные заданными нагрузками и лишними неизвестными Х1, Х2, приложенными в надопорных сечениях В и С.
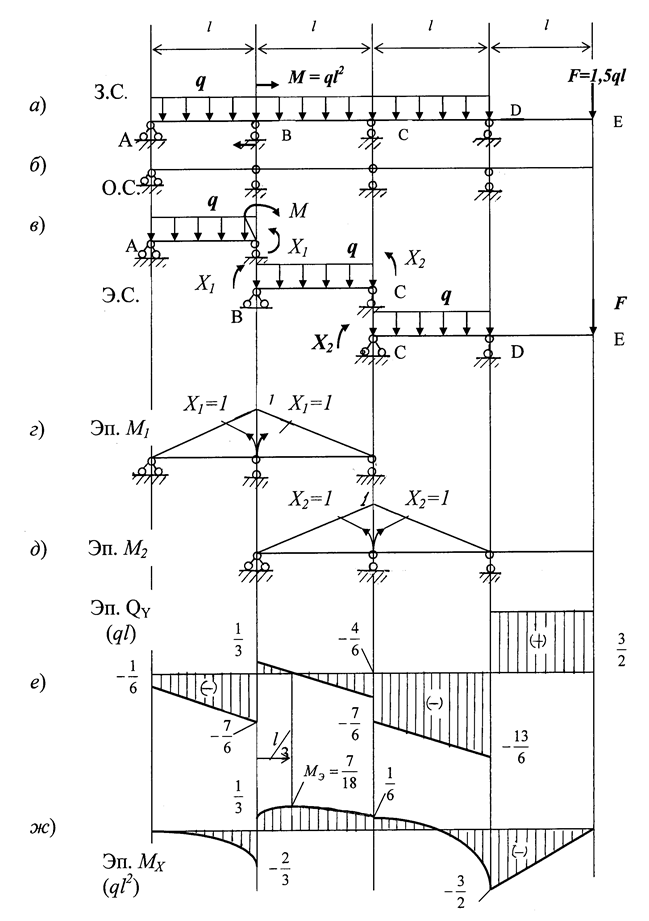
Рис. 1.22
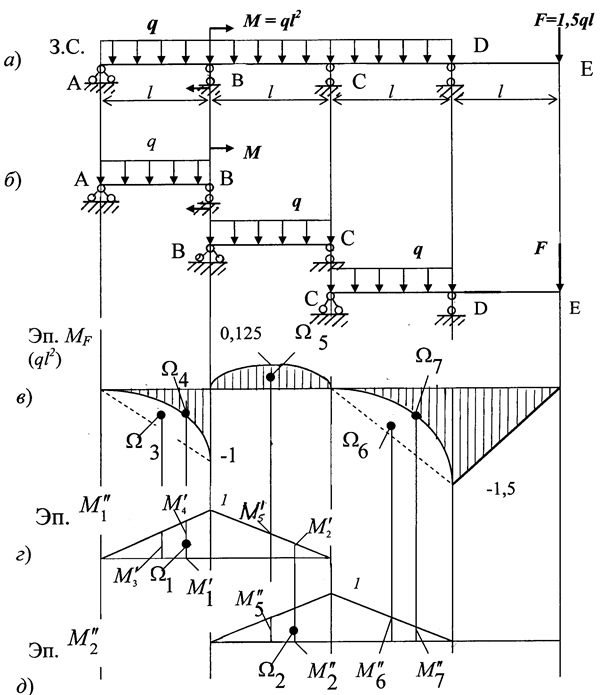
Рис. 1 23
Для определения неизвестных Х1 и Х2 записываем систему двух канонических уравнений метода сил:
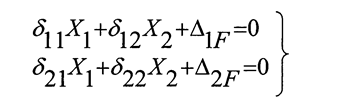
С целью определения коэффициентов этих уравнений поо-чередно нагружаем О.С. единичными нагрузками Х1 = 1, Х2 = 1, внешними нагрузками (q, F) и строим соответствующие эпюры изгибающих моментов М1 (рис. 1.22,г), М2 (рис. 1.22,д) и МF (рис. .23,а,б,в).
Перемножаем эпюру М1 саму на себя. Для этого показываем центр тяжести площади 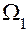 и момент
и момент 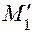 . Используя способ Верещагина, получим:
. Используя способ Верещагина, получим:
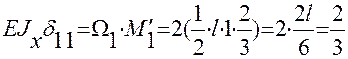 l;
l;
Аналогично, перемножая эпюры 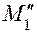 и
и 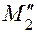 , найдем:
, найдем:
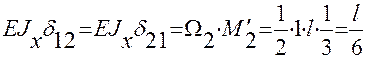 ;
;
Перемножая эпюру 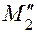 самое на себя, вычисляем
самое на себя, вычисляем 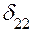 :
:
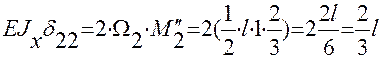 ;
;
Перемножая эпюры от внешних нагрузок (эп. МF) на эпюру 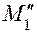 , определим
, определим 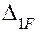 :
:
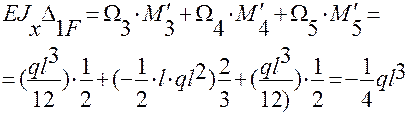 ;
;
Перемножаем эпюры MF и 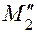 . Напомним, что по способу Верещагина эпюру изгибающих моментов разбивают на простейшие фигуры (треугольник, прямоугольник и т.д.), затем показывают их центры тяжести
. Напомним, что по способу Верещагина эпюру изгибающих моментов разбивают на простейшие фигуры (треугольник, прямоугольник и т.д.), затем показывают их центры тяжести 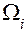 и над ними на эпюре
и над ними на эпюре 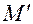 показывают моменты
показывают моменты 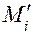 . После этих операций вычисляют:
. После этих операций вычисляют:
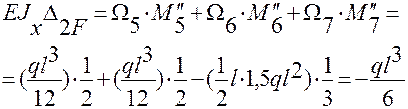 .
.
Знак минус ставится, когда перемножаемые эпюры располагаются по разные стороны от нулевой линии. Подставляем подсчитанные коэффициенты в канонические уравнения:
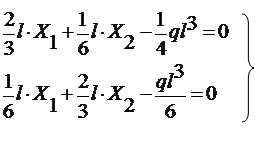
Решая эту систему, находим:
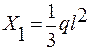 ;
; 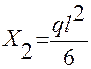 .
.
Далее к каждому участку балки АВ, ВС и СДЕ прикладываем заданные нагрузки и подсчитанные значения лишних неизвестных Х1 и Х2. Строим эпюры изгибающих моментов МХ и поперечных сил QУ на каждом участке балки.
Участок АВ (рис. 1.24 ) ( 0 ≤ z ≤ l ):
Находим реакции опор .
∑mom A = 0; 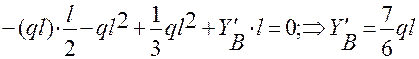 ;
;
∑mom B = 0; 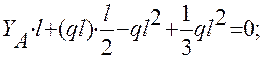 =>
=> 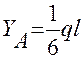 ;
;
Проверка реакций.
∑пр. у =0; 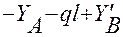 = 0.
= 0.
Строим эпюры .
QY = -YA – qz1;
Т.А z = 0, QY = -YA = - 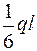 ; т. В z = l,
; т. В z = l, 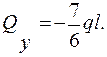
 ;
;
т. А z = 0, МХ =0; т. В z = l, MX = - 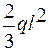 .
.
находим значение МХ при z = 0,5 l, МХ = - 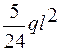 .
.
Участок ВС (рис. 1.25 ) ( 0 ≤ z ≤ l ): 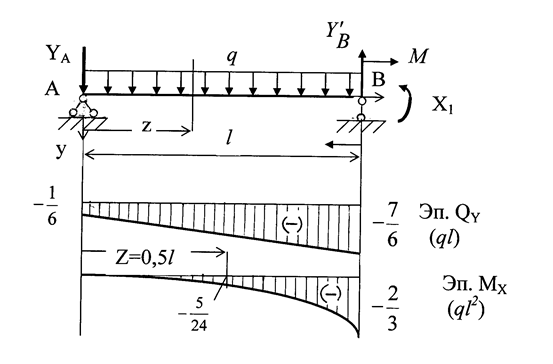
Рис. 1.24
Находим реакции опор.
∑mom B =0; (- 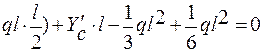 ; =>
; => 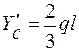 ;
;
∑mom C =0; 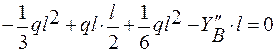 ; =>
; => 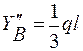 ;
;
Проверка реакций.
∑пр.у = 0; 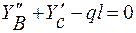 .
.
Строим эпюры QY и MХ .
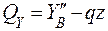 ;
;
Т. В z = 0, 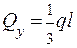 ; т.С z = l,
; т.С z = l, 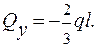
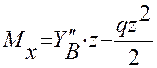 ;
;
Т. В z = 0, 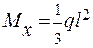 ; т. С z = 0,
; т. С z = 0, 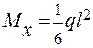 .
.
Точка перегиба.
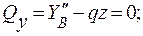 =>
=>  ;
;
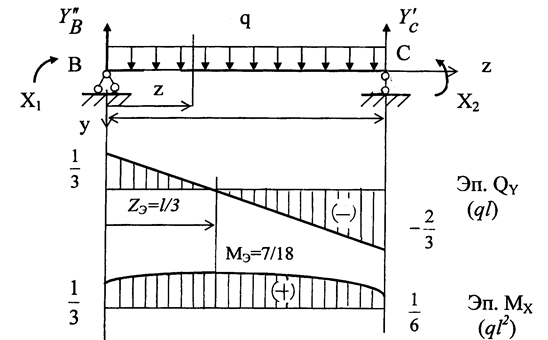
Рис. 1.25
 .
.
Балка СДЕ (рис. 1.26).
Находим реакции опор.
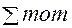 С = 0;
С = 0; 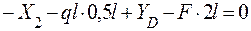 ; =>
; => 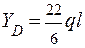 ;
;
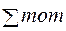 D =0;
D =0; 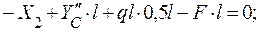 =>
=> 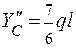 ;
;
Проверка реакций.
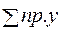 = 0;
= 0; 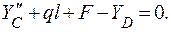
Строим эпюры изгибающих моментов и поперечных сил.
Участок CD ( 0 ≤ z1 ≤ l ):
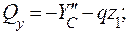
Т.С 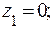
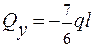 ; т. D z1 =l;
; т. D z1 =l; 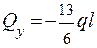 .
.
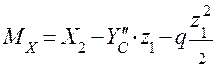 ;
;
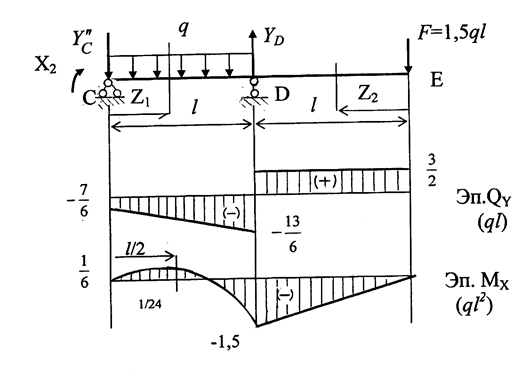
 Рис. 1.26
Рис. 1.26
Т.С z1=0, 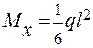 ; т. D z1 = l,
; т. D z1 = l, 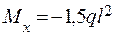 .
.
Значение MX при z1=0,5l: 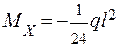 .
.
Участок ED ( 0 ≤ z2 ≤ l ):
QY = F = 1,5ql;
MX = -1,5ql·z2;
Т. Е z2 = 0, MX = 0; т. D z2 = l, MX = -1,5ql.
Результирующие эпюры изгибающих моментов и поперечных сил в балке от заданных нагрузок приведены на рис. 1.22,е,ж.
Проверка правильности решения.
Перемножаем эпюры МХ и М1 (рис. 1.27).
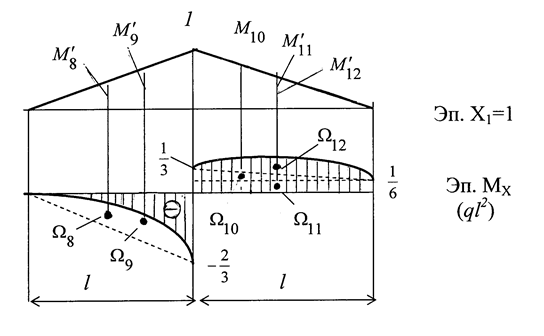
Рис. 1.27
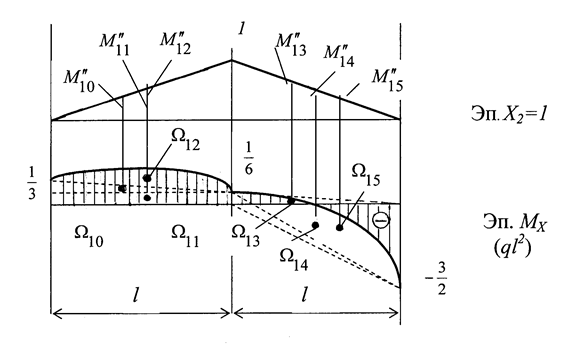
Рис. 1.28
EJXП1 = 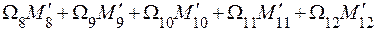 =
=
= 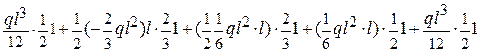 = 0.
= 0.
Перемножаем эпюры МХ и М2 (рис.1.28).
EJXП2 = 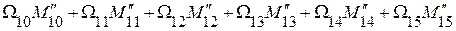 =
=
= 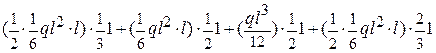 +
+
+( 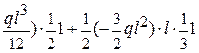 = 0.
= 0.
Подбираем размер поперечного сечения балки.
Из эпюры изгибающих моментов в МХ находим:
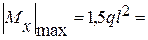 1,5·25·103 ·0,62=13500(Нм).
1,5·25·103 ·0,62=13500(Нм).
Необходимый момент сопротивления сечения балки равен:
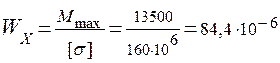 м3 = 84,4 см3.
м3 = 84,4 см3.
Подбираем сечение двутавра по ГОСТ 8239-89 № 16 , имеющей момент сопротивления WX = 109см3.
ЗАДАЧА 1.6.
Для показанной на рис. 1.29 рамы (З.С.) построить эпюры изгибающих моментов МХ и поперечных QY сил. Определить для узла С горизонтальное перемещение fгор.
|
|
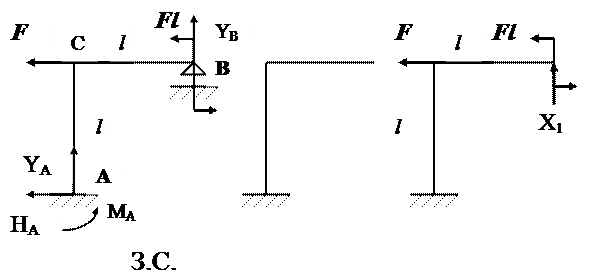
Рис. 1. 29
Решение
Определяем степень статической неопределимости рамы. В опорах возникают четыре опорные реакции. Тогда степень стати-ческой неопределимости S равна:
S = 4 – 3 = 1.
Решаем задачу методом сил. Выбираем основную систему (О.С.), отбрасывая опору В и снимая все нагрузки.
Загружаем (О.С.) заданными нагрузками и «лишней» неизве-стной Х1 , приложенной вместо опоры В. Получаем эквивалентную систему (Э.С.).
Каноническое уравнение имеет вид:
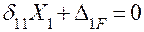 .
.
Для определения коэффициентов уравнения 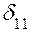 и
и 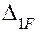 строим эпюры изгибающих моментов от Х1 = 1 (Эп. М1) и заданных нагрузок (Эп. MF) рис. 1.30.
строим эпюры изгибающих моментов от Х1 = 1 (Эп. М1) и заданных нагрузок (Эп. MF) рис. 1.30.
Построение эпюры изгибающих моментов от заданных сил.
Участок ВС (0 ≤ Z1 ≤ l ):
МХ = Fl .
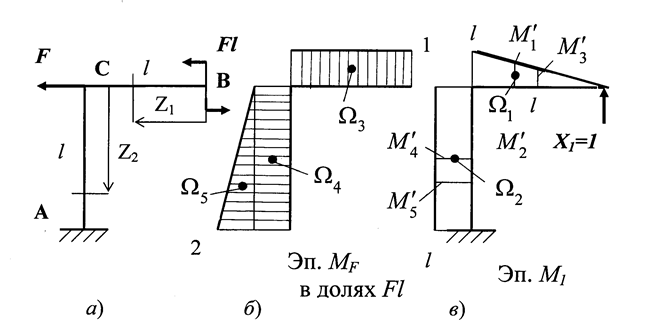
Рис. 1. 30
Участок СА ( 0 ≤ Z2 ≤ l):
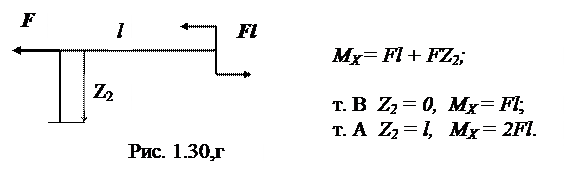
По найденным значениям MX строим эпюру изгибающих мо-ментов (Эп. MF).
Перемножаем эпюру от М1 саму на себя и находим коэффициент 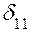 :
:
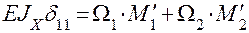 =
= 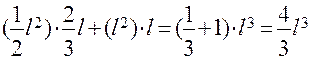 .
.
Перемножаем эпюру от заданных нагрузок (Эп. MF) на эпюру от единичной силы (Эп. M1) и находим коэффициент 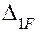 :
:
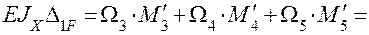
= 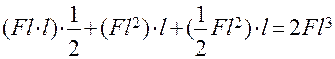 .
.
Определяем значение «лишней» неизвестной Х1:
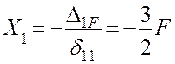 .
.
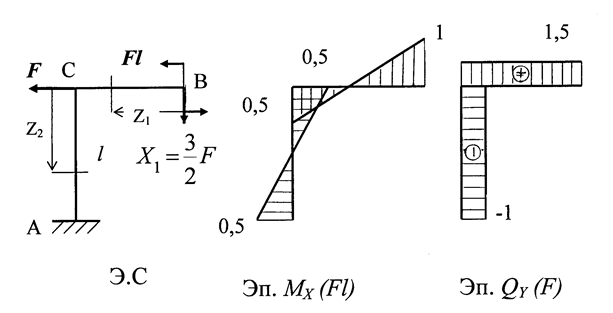
Рис. 1. 31
Прикладываем в эквивалентной системе силу Х1 с учетом знака и строим эпюры изгибающих моментов МХ и поперечных сил QY.
Участок СВ (0 ≤ Z1 ≤ l):
MX = Fl – 1,5F·Z1;
т. В Z1 = 0, MX = Fl; т.С Z2 = l, MX = -0,5Fl.
Участок СА (0 ≤ Z2 ≤ l):
MX = Fl – 1,5Fl + F·Z2;
т. С Z2 = 0, MX = - 0,5Fl; т. A Z2 = l, MX = 0,5Fl.
Соответствующие эпюры МХ и QY показаны на рис. 1.31.
Проверка решения. Перемножаем построенную эпюру МХ на единичную эпюру (Эп. М1), показанные на рис. 1.32 .
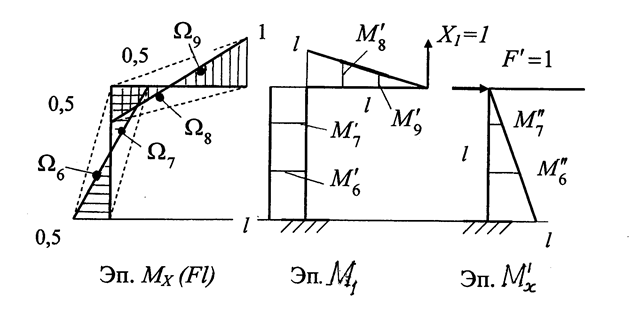
Рис. 1.32
EJX П = 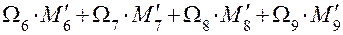 =
=
= 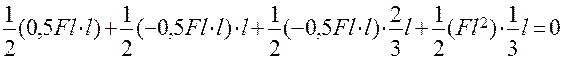 .
.
Определение перемещения узла С в горизонтальном направлении - fгор. К основной системе в узле С рамы в заданном направлении приложим силу F1 = 1.
Построим эпюру изгибающих моментов 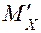 . Методом Мора, используя правило Верещагина, вычисляем перемещение fгор .
. Методом Мора, используя правило Верещагина, вычисляем перемещение fгор .
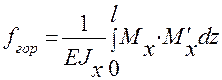 =
= 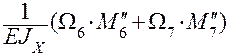 =
=
= 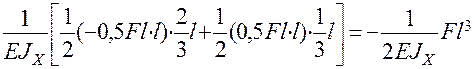 .
.
Знак минус в полученном выражении означает, что перемещение узла С рамы происходит в противоположном направлении к принятому направлению  = 1.
= 1.
ЗАДАЧА 1.7.
Для, показанной на рис. 1.33 рамы построить эпюры изгибающих моментов и поперечных сил, а также подобрать размеры прямоугольного сечения с размерами h и b (h=2b).
Дано: F = 1,5ql, q =25кН/м, l=0,6м.
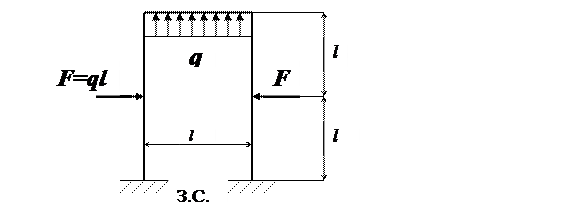
Рис. 1.33
Решение
Рама имеет две опоры – жесткие заделки. В каждой из них возникают три реакции – момент, горизонтальная и вертикальная силы. Таким образом получаем шесть реакций. Вычитая три урав-нения статики, устанавливаем, что рама три раза статически неоп-ределима S = 3.
Однако рама, вместе с приложенными нагрузками, обладает симметрией относительно вертикальной оси. В этом случае если разрезать раму при выборе основной системы по оси симметрии, то вместе разреза будут возникать только две «лишние» неизвестные Х1 и Х2, а кососимметричные неизвестные Х3 равны нулю. Таким образом получаем, что данная рама с приложенными к ней нагрузками два раза статически неопределима. На рис. 1.34 показана основная система (О.С.) – рама разрезана по оси симметрии и эквивалентная система (Э.С.), когда к основной системе приложены лишние неизвестные Х1, Х2 и заданные нагрузки - сосредоточенная сила F и распределенная нагрузка q.
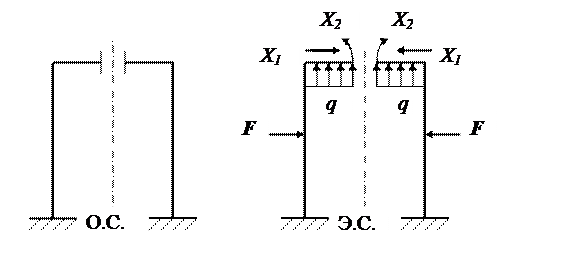
Рис. 1.34
Записываем систему канонических уравнений метода сил:
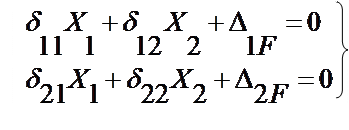
Для определения коэффициентов канонических уравнений строим эпюры изгибающих моментов от Х1 =1, Х2 =1 и заданных нагрузок, которые обозначены М1, М2, МF и показаны на рис. 1.35.
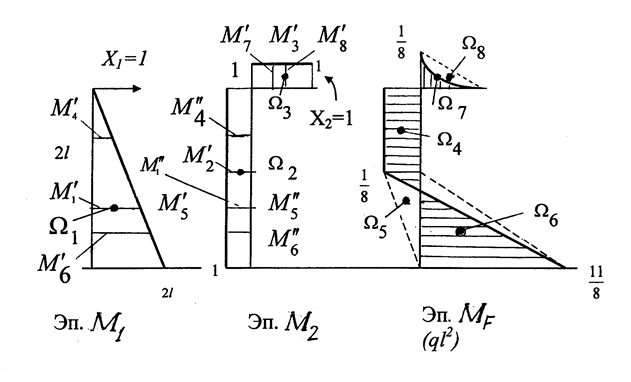 Рис. 1.35
Рис. 1.35
Перемножаем эпюру М1 самое на себя:
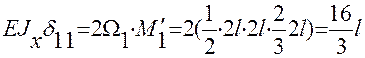 ;
;
Перемножаем эпюру М1 на эпюру М2:
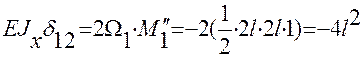 ;
;
Перемножаем эпюру М2 самое на себя:
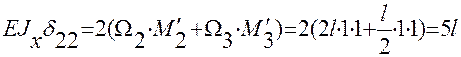 ;
;
Перемножаем эпюру М1 на эпюру МF:
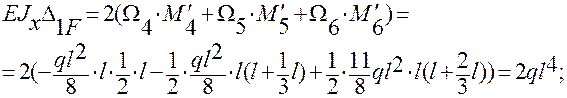
Перемножаем эпюру М2 на эпюру МF:
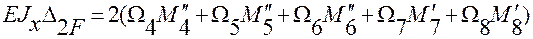 =
=
=2( 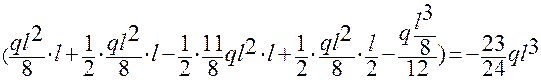 .
.
Подставляем полученные значения коэффициентов в кано-нические уравнения, решаем систему и находим значения «лишних» неизвестных Х1 и Х2.
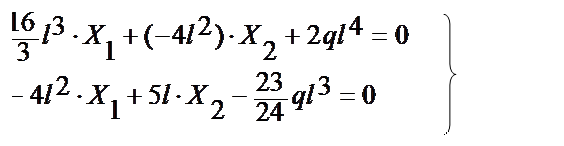
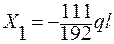 ;
; 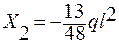 .
.
Прикладываем Х1 и Х2 с учетом знаков к эквивалентной системе и строим эпюры изгибающих моментов и поперечных сил (рис. 1.36).
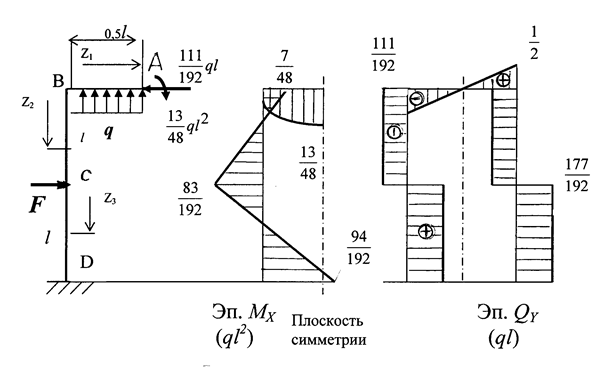
Рис. 1.36
Участок АВ ( 0 ≤ z1 ≤  ):
):
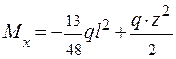 ;
;
т. A 
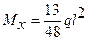 ; т. В
; т. В 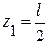 ;
; 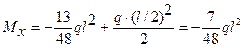 .
.
Qy = -q·z1;
т. А z1 = 0; Qy = 0; т. В z1 = l/2; Qy = 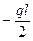 .
.
Участок ВС  ( 0 ≤ z2 ≤ l ):
( 0 ≤ z2 ≤ l ):
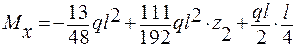 ;
;
т. В z2 = 0; 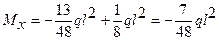 ;
;
т. С z2 = l; 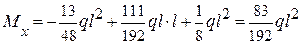 .
.
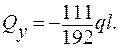
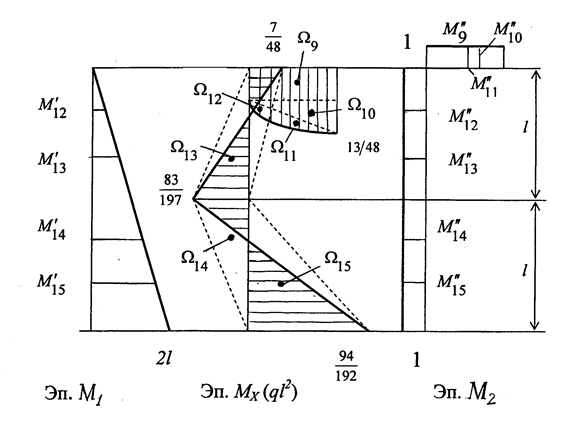
Рис. 1.37
Участок СД ( l ≤ z3 ≤ 2l ):
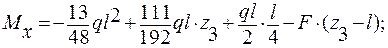
т. С z3 = l; 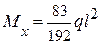 ;
;
т. D z3 = 2l; 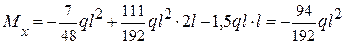 .
.
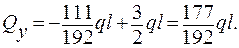
Выполним проверку правильности решения задачи. Перемножим полученную эпюру изгибающих моментов МХ на эпюры от М1 и М2.
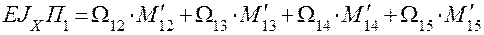 =
=
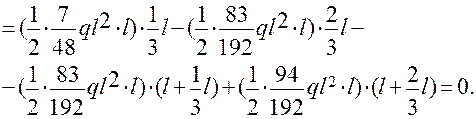
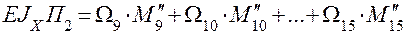 =
= 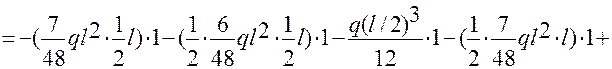
+ 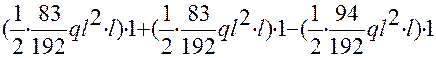 = 0.
= 0.
Задача решена верно.
Определим размеры прямоугольного сечения рамы.
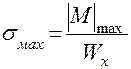 .
.
Приравнивая 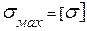 = 100МПа;
= 100МПа; 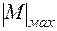 =
= 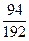 ql2; q =25кН/м; l =0,6м, и зная WX = (b·h2)/12 и h = 2b,
ql2; q =25кН/м; l =0,6м, и зная WX = (b·h2)/12 и h = 2b,
получим: 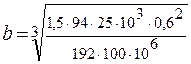 . b=4·10-2 м, h = 8·10-2м.
. b=4·10-2 м, h = 8·10-2м.
ЗАДАЧА 1.8.
Построить эпюру изгибающих моментов для рамы, показанной на рис. 1.38.
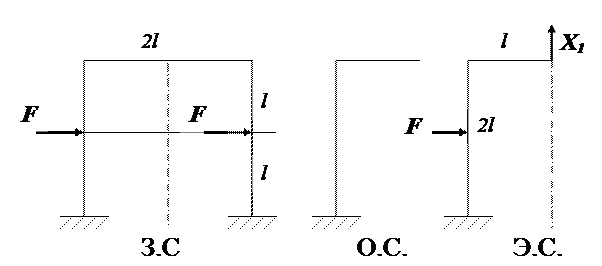
Рис. 1.38
Данная рама имеет геометрическую ось симметрии и нагружена– кососимметричными силами F. Поэтому при ее разрезании, по оси симметрии, как показано на рисунке, все симметричные силовые факторы равны нулю. Таким образом, задача один раз статически неопределима.
Каноническое уравнение метода сил:
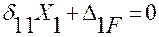 .
.
Для вычисления коэффициентов этого уравнения строим эпюры изгибающих моментов от «лишней» неизвестной Х1 = 1 и внешних сил - силы F . Эпюры М1 и МF даны на рис. 1.39.
Вычисляем значения коэффициентов этого уравнения.
Перемножаем эпюру М1 самое на себя:
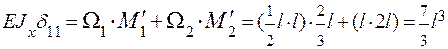 .
.
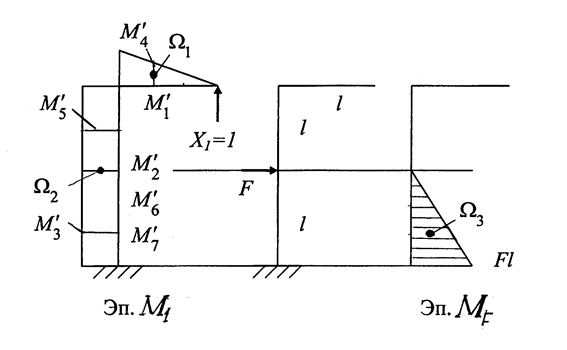
Рис. 1.39
Перемножаем эпюру МF на эпюру М1:
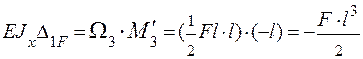 .
.
Тогда 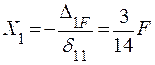 .
.

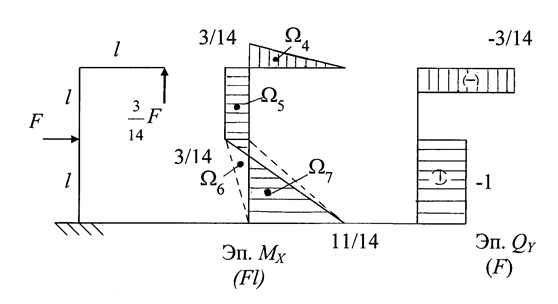
Рис. 1.40
Строим эпюры изгибающих моментов МХ и поперечных сил QY от заданной силы F и подсчитанной «лишней» неизвестной Х1 (рис. 1.40).
Проверка правильности решения задачи. Перемножаем эпюру МХ на эпюру М1.
EJX П1 = 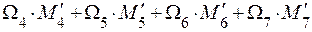 =
=
= 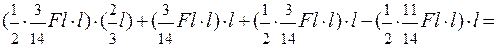 0.
0.
Задача решена верно.
Дата: 2016-10-02, просмотров: 292.