Типы данных, СД и АТД
Тип данных - это множество значений, которые может принимать переменная, и множество операций, которые можно выполнять над этими переменными. Набор базовых типов данных отличается в различных языках.
Абстрактный тип данных (АТД) - это математическая модель плюс различные операторы, определенные в рамках этой модели.
Для представления АТД используются структуры данных (СД), которые представляют собой набор переменных, возможно, различных типов данных, объединенных определенным образом.
Базовым строительным блоком СД является ячейка, которая предназначена для хранения значения определенного базового или составного типа данных. СД создаются путем задания имен совокупностям (агрегатам) ячеек и интерпретации значения некоторых ячеек как указателей на другие ячейки.
В качестве простейшего механизма агрегирования ячеек в большинстве языков программирования можно применять (одномерный) массив, т.е. последовательность ячеек определенного типа.
Другим общим механизмом агрегирования ячеек в языках программирования является структура (запись). Запись можно рассматривать как ячейку, состоящую из нескольких других ячеек (называемых полями), значения в которых могут быть разных типов.
Массивы и записи являются структурами с произвольным доступом, подразумевая под этим, что время доступа к компонентам массива или записи не зависит от значения индекса массива или указателя поля записи.
Третий метод агрегирования ячеек, который можно найти в языках программирования, это файл. Файл, как и одномерный массив, является последовательностью значений определенного типа. Различают файлы прямого и последовательного доступа. В файле прямого доступа имеется индекс, т.е. все ячейки (компоненты) файла пронумерованы. Доступ может быть осуществлен к любой ячейке. Файл последовательного доступа не имеет индексов: его элементы доступны только в том порядке, в каком они были записаны в файл.
Достоинство агрегирования с помощью файла заключается в том, что файл не имеет ограничения на количество составляющих его элементов, и это количество может изменяться во время выполнения программы.
В дополнение к средствам агрегирования ячеек в языках программирования можно использовать указатели и курсоры. Указатель - это ячейка, чье значение указывает на другую ячейку. При графическом представлении СД в виде схемы тот факт, что ячейка А является указателем на ячейку В, показывается с помощью стрелки от ячейки А к ячейке В.
Курсор - это ячейка с целочисленным значением, используемая для указания на массив. В качестве способа указания курсор работает так же, как и указатель, но курсор можно использовать и в языках, которые не имеют явного типа указателя.
В схемах структур данных принято рисовать стрелку из ячейки курсора к ячейке, на которую указывает курсор. Иногда также указывают целое число в ячейке курсора, напоминая тем самым, что это ненастоящий указатель.
Пример СД представлен на рис.2.9.
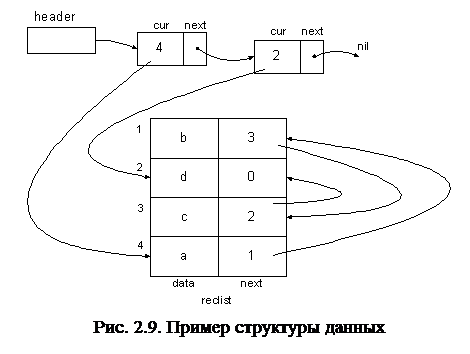 |
В данной структуре ячейка header содержит указатель на запись, состоящую из двух полей: cur и next. Поле cur содержит курсор, содержащий индекс логически первого элемента массива reclist (в данном случае четвертый элемент массива является логически первым). Поле next содержит указатель на аналогичную запись, в которой поле cur содержит курсор на логически последнюю запись массива reclist (в примере это вторая запись), а поле next содержит пустой указатель. Массив reclist состоит из четырех записей с индексами от 1 до 4. Каждая запись состоит из двух полей: data и next. Поле data содержит данные (в примере это символы a,b,c,d). Логический порядок элементов массива определяется значением курсора в поле next - курсор хранит индекс логически следующего элемента массива. Так за четвертым элементом следует первый, за первым - третий, за третьим - второй. Второй элемент массива логически последний, т.к. значение поля next второго элемента равно 0, т.е. отличается от любого значения индекса массива - 1,2,3 или 4.
Время выполнения программ
В зависимости от выбранных структур данных может меняться время выполнения программ. В данном курсе, как правило, приводятся временные оценки алгоритмов без доказательства. Рассмотрим общепринятые временные оценки алгоритмов.
Время выполнения программы обычно определяют как функцию от длины исходных данных. Обычно говорят, что время выполнения программы выражается функцией T(n) от входных данных размера n.
Для многих программ время выполнения является функцией входных данных, а не их размера. В этом случае T(n) определяется как функция времени выполнения программы в наихудшем случае, т.е. как максимум времени выполнения по всем входным данным размера n. Также иногда рассматривают Tср(n) как среднее время выполнения по всем входным данным размера n. На практике среднее время найти сложнее, чем наихудшее.
Считается, что все функции времени определены на множестве неотрицательных целых чисел, и их значения также неотрицательны, но необязательно целые.
Для описания скорости роста функций времени выполнения программ используется O-символика. Например, когда говорят, что время выполнения T(n) некоторой программы имеет порядок O(n2) (читается «о-большое от n в квадрате» или «о от n в квадрате»), то подразумевают, что существуют положительные константы c и n0 такие, что для всех n³n0 выполняется неравенство T(n)£ T¢(n), где T¢(n)=c×n2.
Пример. Пусть T1(n)=(n+5)2. Тогда T1(n) будет иметь порядок O(n2). Действительно, если положить n0=1 и c=37, то легко показать, что для n³1 будет выполняться неравенство (n+5)2£T2(n), T2(n)=36×n2.
В общем случае будем говорить, что T(n) имеет порядок O(f(n)), если существуют положительные константы c и n0 такие, что для всех n³n0 выполняется неравенство T(n)£c×f(n).
Пример. Пусть T3(n)=3×n3+2×n2. Данная функция имеет порядок O(n3). Действительно, если положить n0=0 и c=5, то легко показать, что для n³0 будет выполняться неравенство 3×n3+2×n2£5×n3. Можно сказать, что T3(n)=3×n3+2×n2 имеет порядок O(n4), но это более слабое утверждение, чем то, что T3(n)=3×n3+2×n2 имеет порядок O(n3).
Применение O-символики для оценок времени выполнения алгоритмов чаще предпочтительнее, чем использование конкретных функций времени. Однако, для оценки реальных программ, т.е. программ работающих с данными ограниченного размера, нужно учитывать вид конкретных функций времени.
Пример. Пусть одна и та же задача может быть решена с помощью двух программ P1, P2 или P3, имеющих функции времени T1(n)=(n+5)2, T2(n)=36×n2, T3(n)=3×n3+2×n2 соответственно. Значения данных функций для различных значений n сведены в табл.2.3. Из таблицы видно, что функция T3(n) для n=1 и n=2 имеет меньшее значение, чем функция T1(n). Поэтому, несмотря на то, что функция T3(n) имеет порядок O(n3), а функция T1(n) - O(n2), использование программы P3 при n=1 и n=2 более предпочтительно, чем использование программы P1. Также функция T3(n) для n=1,2,…,11 имеет меньшее значение, чем функция T2(n). Поэтому для n=1,2,…,11 предпочтительнее использовать программу PЗ, чем программу P2, несмотря на то, что порядок функции T3(n) - O(n3), а функция T2(n) - O(n2).
| Таблица 2.3 | |||||||
| Значения функций времени выполнения программ | |||||||
| n | T1(n)= (n+5)2 | T2(n)= 36×n2 | T3(n)= 3×n3+2×n2 | n | T1(n)= (n+5)2 | T2(n)= 36×n2 | T3(n)= 3×n3+2×n2 |
Списки
Список представляет собой последовательность элементов определенного типа. Список представляется в виде последовательности элементов, разделенных запятыми: a1,a2,...,an, где n³0, и все ai имеют некоторый тип elementtype. Количество элементов n называют длиной списка. Если n³1, то a1 называется первым элементом, а an - последним элементом списка. В случае n=0 имеем пустой список, который не содержит элементов.
Важное свойство списка заключается в том, что его элементы можно линейно упорядочить в соответствии с их позицией в списке. Говорят, что элемент ai предшествует ai+1 для i=1,2,...,n-1 и ai следует за ai-1 для i = 2,3,...,n. Также говорят, что элемент ai имеет позицию i.
Определим множества операторов списка. При этом будем использовать следующие обозначения: L - список объектов типа elementtype, x - объект типа elementtype, р - позиция элемента в списке. Обычно позиции - это целые положительные числа, но на практике могут встретиться другие представления.
1. INSERT(x,p,L). Этот оператор вставляет объект x в позицию p в списке L, перемещая элементы от позиции p и далее в следующую, более высокую позицию. Таким образом, если список L состоит из элементов a1,a2,...,an, то после выполнения этого оператора он будет иметь вид a1,a2,..., ap-1,x,ap,...,an. Если p принимает значение ENDLIST, равное n+1, то будем иметь a1,a2,...,an,x. Если в списке L нет позиции p, и p не равно ENDLIST, то результат выполнения этого оператора не определен.
2. LOCATE(x,L). Эта функция возвращает позицию объекта x в списке L. Если в списке объект x встречается несколько раз, то возвращается позиция первого от начала списка объекта x. Если объекта x нет в списке L, то возвращается ENDLIST.
3. RETRIEVE(p,L). Эта функция возвращает элемент, который стоит в позиции p в списке L. Результат не определен, если в списке L нет позиции p. Отметим, что элементы должны быть того типа, который в принципе может возвращать функция. Однако на практике мы всегда можем изменить эту функцию так, что она будет возвращать указатель на объект типа elementtype.
4. DELETE(p,L). Этот оператор удаляет элемент в позиции p списка L. Так, если список L состоит из элементов a1,a2,...,an, то после выполнения этого оператора он будет иметь вид a1,a2,...,ap-1,ap+1,...,an. Результат не определен, если в списке L нет позиции p или p=ENDLIST.
5. NEXT(p,L) и PREVIOUS(p,L). Эти функции возвращают соответственно следующую и предыдущую позиции от позиции p в списке L. Если p - последняя позиция в списке L, то NEXT(p,L)= ENDLIST. Функция NEXT не определена, когда p=ENDLIST, или в списке L нет позиции p. Функция PREVIOUS не определена, если р=1, или в списке L нет позиции p.
6. NULLIST(L). Эта функция делает список L пустым и возвращает позицию ENDLIST.
7. FIRST(L), LAST(L). Эти функции возвращают соответственно первую и последнюю позиции в списке L.
8. PRINTLIST(L). Печатает элементы списка L в порядке их расположения.
9. EMPTYLIST(L). Эта функция возвращает значение true (истина), если список L пустой и значение false (ложь) в противном случае.
Реализация списков
В этом разделе речь пойдет о нескольких структурах данных, которые можно использовать для представления списков. Будут рассмотрены реализации списков с помощью массивов и указателей. Каждая их этих реализаций осуществляет определенные операторы, выполняемые над списками более эффективно, чем другая.
Дата: 2016-09-30, просмотров: 388.