Любой граф может быть представлен в матричной форме.
Матрицей смежности графа G=(V,E) называется матрица A порядка n´n, где n=|V|. Элемент матрицы смежности аij=1, если (vi,vj)ÎЕ, vi,vjÎV, и aij=0, если (vi,vj)ÏЕ.
Для графа, изображенного на рис. 2.17, матрица смежности представлена в таблице 2.4.
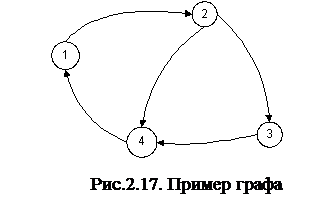 |
Отметим, что для неориентированных графов матрица смежности симметрична относительно главной диагонали, то есть в памяти ЭВМ достаточно хранить только половину матрицы.
| Таблица 2.4. | |||||
| Матрица смежности графа, изображенного на рис.2.17 | |||||
Матрицей инцидентности графа G=(V,E) называется матрица B порядка n´m, где n=|V|, m=|E|. Элементы матрицы инцидентности bij определяются следующим образом: bij=1, если i-я вершина является началом j-ой дуги, bij=-1, если i-я вершина является концом j-ой дуги, bij=0, если i-я вершина и j-я дуга не инцидентны.
Для неориентированных графов в матрице инцидентности элементам достаточно присваивать только два символа (1 и 0).
Для графа, представленного на рис. 2.17, матрица инцидентности показана в таблице 2.5.
| Таблица 2.5. | ||||||
| Матрица инцидентности графа, изображенного на рис.2.17 | ||||||
| -1 | ||||||
| -1 | ||||||
| -1 | ||||||
| -1 | -1 | |||||
Заметим, что с помощью матрицы инцидентности не могут быть закодированы петли графа. В свою очередь, в матрице смежности теряется информация о кратных рёбрах (параллельных дугах). Поэтому в некоторых случаях требуется отходить от определений и вводить дополнительные СД.
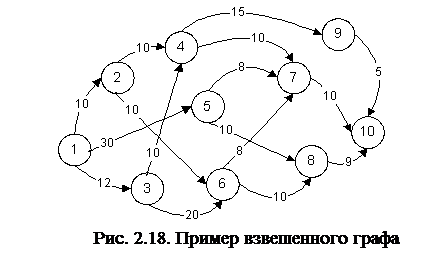
При кодировании взвешенного графа вместо единичных элементов матрицы смежности удобно записать веса соответствующих дуг, а веса несуществующих дуг полагать равными бесконечности (обозначение ¥). Отметим, что при реализации на ЭВМ вместо бесконечности используют максимально возможное значение типа, используемого для элементов матрицы. Такая матрица называется матрицей весов. Матрица весов для графа, представленного на рис.2.18, приведена в таблице 2.6.
На практике очень часто матрицы, представляющие графы, бывают сильно разряженными, то есть содержат много символов «0» или «¥«. Это приводит к неоправданным затратам памяти при хранении этих матриц в ЭВМ.
Объем памяти можно существенно уменьшить, если упаковывать матрицы в массивы смежности. Пример упаковки рассмотренной матрицы весов (табл. 2.6) в массивы приведен на рис. 2.19.
 |
Упаковка осуществляется с помощью трех массивов: S, V и U. Заполнение массивов S и V осуществляется путем построчного просмотра матрицы. При просмотре текущей строки матрицы в массиве S сохраняются номера столбцов, содержащие значения, отличные от ¥, сами значения сохраняются в массиве V. Массив U служит для разграничения информации в массивах S и V, i-ый элемент массива U содержит индекс массивов S и V, с которого начинается информация, относящаяся к i-ой строке матрицы. Таким образом, для нахождения вершин, смежных i-ой вершине, и весов соответствующих дуг по массивам смежности необходимо вычислить начальный In и конечный Ik индексы в массивах V и S по формулам: In=Ui; Ik=Ui+1-1. Тогда SIn,SIn+1,…,SIk - вершины, смежные i-ой вершине, VIn,VIn+1,…,VIk – длины дуг (i,SIn),(i,SIn+1,),…,(i,SIk). Если Ik=Ui+1-1 окажется меньше In=Ui, то это означает, что i-я строка матрицы весов содержит одни ¥, т.е. i-я вершина не имеет смежных вершин.
Для хранения упакованной таким образом матрицы весов понадобится 43 ячейки памяти, занимаемых массивами V,S и U. Неупакованная матрица занимала 10×10=100 ячеек памяти.
Если упаковывается матрица смежности, то массив V не нужен.
| Таблица 2.6. | |||||||||
| Матрица весов графа, изображенного на рис.2.18 | |||||||||
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | |||
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ||
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ||
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ||
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ||
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ||
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | |
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | |
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | |
| ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| V | |||||||||||||||||
| S | |||||||||||||||||
| U | |||||||||||||||||
| Рис.2.19. Упаковка матрицы весов (табл. 2.6) в массивы смежности |
Еще один способ хранения графов - это массив рёбер, то есть массив записей, в котором перечислены все рёбра графа (каждая запись кодирует ребро). Массив рёбер графа, представленного на рис. 2.18, приведен на рис. 2.20. Здесь массив занимает 48 ячеек.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | ||
| I | |||||||||||||||||
| J | |||||||||||||||||
| V | |||||||||||||||||
| I - начальная вершина, J – конечная вершина, V – вес дуги (I,J) | |||||||||||||||||
| Рис.2.20. Список рёбер графа, изображенного на рис.2.18 |
При реализации алгоритмов, в которых изменяется исходный граф, например, добавляются или удаляются вершины, для хранения графов иногда удобно применять списки смежности. Списки смежности представляют собой линейный список из n элементов, где n - число вершин графа (главный список). В качестве элементов главного линейного списка выступают подчиненные линейные списки. В i-ом подчиненном списке число элементов равно числу вершин, смежных i-ой вершине графа. Каждый такой элемент хранит номер вершины (j), смежной i-ой вершине графа. Если граф взвешенный, то также хранится вес соответствующей дуги (i,j).
Для графа, изображенного на рис. 2.18, список смежности представлен на рис. 2.21.
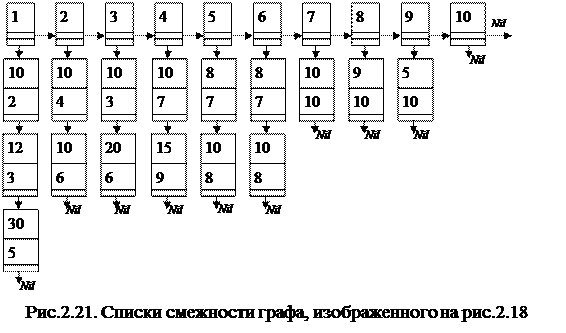 |
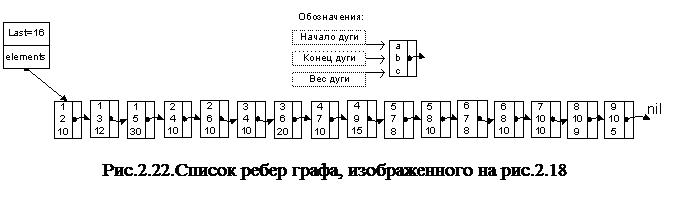
Еще один способ хранения графов - это список рёбер, то есть список, в котором перечислены все рёбра графа. Список рёбер графа, представленного на рис. 2.18, приведен на рис. 2.22.
 |
Естественно, что рассмотренные способы хранения взвешенных графов пригодны и для хранения невзвешенных графов. При хранении невзвешенных графов ячейки, предназначенные для хранения веса ребра, становятся ненужными.
Выбор того или иного способа кодирования графа и СД для его реализации зависит от конкретной задачи, алгоритма её решения, возможных входных данных и других факторов.
Теперь рассмотрим один из способов хранения ориентированных деревьев. Поскольку дерево является частным случаем графа, то для его хранения подойдет любая из рассмотренных структур хранения графов.
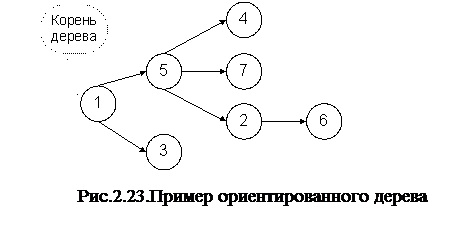
Например, дерево, изображенное на рис.2.23, может быть сохранено матрицей смежности, представленной в табл.2.7. К недостаткам такого способа следует отнести то, что получаемые матрицы, как правило, сильно разряженные, и занимают большой объем памяти. Как было сказано выше, объем памяти можно уменьшить, если упаковать матрицу в массивы смежности. Для рассматриваемого примера такие массивы представлены на рис.2.24.
 |
| Таблица 2.7. | ||||||||
| Матрица смежности дерева, изображенного на рис.2.23 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| S | ||||||||
| U | ||||||||
| Рис.2.24. Упаковка матрицы смежности (табл. 2.7) в массивы смежности |
Есть еще один более существенный недостаток. Этот недостаток заключается в трудности восстановления путей, ведущих в вершины дерева из его корня (из вершины, в которую нет входящих дуг). Действительно, в рассматриваемом примере при восстановлении пути из вершины 1 (корень) в вершину 6 (путь 1,5,2,6) возникает неоднозначность - куда двигаться из вершины 1 в 3 или 5 вершину. Аналогично из 5 вершины не ясно, куда двигаться в 2,4 или 7 вершины. Такие неоднозначности приводят к итерационному алгоритму восстановления путей, что является существенным недостатком.
Наиболее выгодно ориентированное дерево, состоящее из n вершин, пронумерованных числами 1,2,...n, сохранить в массиве P из n ячеек, также пронумерованных числами 1,2,...n. Элементы массива P формируются следующим образом: Pi=номер вершины, предшествующей вершине i, если такая вершина есть, и Pi=0 в противном случае (вместо нуля можно использовать любое число, не использующееся для нумерации вершин дерева). Для дерева, представленного на рис. 2.23, такой массив представлен на рис.2.25.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| P | |||||||||
| Рис.2.25. Массив для хранения дерева, изображенного на рис.2.23 | |||||||||
Если дерево хранится в таком массиве, то путь w из корня k в некоторую вершину v легко восстановить с конца, т.е. в обратном порядке от вершины v к вершине k:
w=v, P[v], P[P[v]], P[P[P[v]]],...,k.
При восстановлении пути из вершины 1 в вершину 6 для рассматриваемого дерева получим следующую последовательность действий: v=6, P[6]=2, P[2]=5, P[5]=k=1. Итак, w=6,2,5,1. Перевернув последовательность w, получим искомый путь 1,5,2,6. Восстановление пути удобно осуществлять с помощью стека. Разработайте алгоритм восстановления пути самостоятельно.
Вопросы для повторения
1. Понятие экономической информации.
2. Фазы существования информации.
3. Понятие сигнала.
4. Понятие дискретизации сигналов.
5. Мера количества информации.
6. Понятие бита, байта, килобайта и мегабайта.
7. Понятие избыточности текста.
8. Понятие удельной информативности (энтропии).
9. Понятие кодирования информации и кода.
10. Запись натурального числа в двоичной системе как пример простейшего кода.
11. Способы порождения кодовых слов в порядке двоичного счета.
12. Понятие кода Грэя
13. Способ порождения кода Грэя.
14. Сущность оптимального кодирования.
15. Понятие средней длины кода.
16. Сущность помехозащищенного кодирования. Код с проверкой на четность.
17. Понятие типа данных, СД, АТД.
18. Оценка времени выполнения программ. О-символика.
19. Понятие АТД «Список».
20. Реализация списков посредством массивов.
21. Реализация списков с помощью указателей.
22. Понятие АТД «Стек».
23. Понятие АТД «Очередь».
24. Основные понятия теории графов.
25. Представление графов в памяти ЭВМ с помощью матриц смежности.
26. Представление графов в памяти ЭВМ с помощью матриц инцидентности.
27. Представление взвешенных графов в памяти ЭВМ с помощью матриц весов.
28. Представление графов в памяти ЭВМ с помощью массивов смежности.
29. Представление графов в памяти ЭВМ с помощью массивов ребер.
30. Представление графов в памяти ЭВМ с помощью списков смежности.
31. Представление графов в памяти ЭВМ с помощью списков ребер.
32. Представление ориентированных деревьев в памяти ЭВМ с помощью массивов.
Резюме по теме
Рассмотрены основные понятия теории информации и методы организации данных в памяти ЭВМ.
Дата: 2016-09-30, просмотров: 333.