В процессе передачи и хранения информации, представленной в двоичном коде, могут возникнуть ошибки, связанные с изменением отдельных символов (0 вместо 1 и 1 вместо 0), вследствие действия помех. Обеспечить помехоустойчивость можно, применяя корректирующие или помехозащищенные коды, позволяющие обнаруживать или исправлять возникающие ошибки.

Проиллюстрируем идею построения помехозащищенных кодов на геометрической модели n-элементного двоичного кода. Такой код представим в виде n-мерного куба (гиперкуба), каждая из вершин которого соответствует одной из 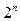возможных кодовых комбинаций, и две вершины соединены ребром, если соответствующие им кодовые комбинации отличаются одним элементом, длина каждого ребра равна единице. На рис. 2.7 представлен трехмерный куб.

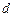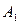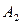Кодовым расстоянием ( ) чисел и называется число разрядов (символов), в которых 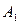отличается от 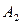. В геометрической интерпретации кодовое расстояние - это минимальное число ребер в n-мерном кубе, разделяющих вершины соответствующие числам 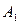и .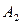

Если все 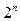кодовых комбинаций разрешены, то кодовое расстояние между соседними комбинациями 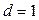. В этом случае отсутствует какой либо признак, позволяющий судить о появлении ошибки в кодовой комбинации, и код не является помехозащищенным.

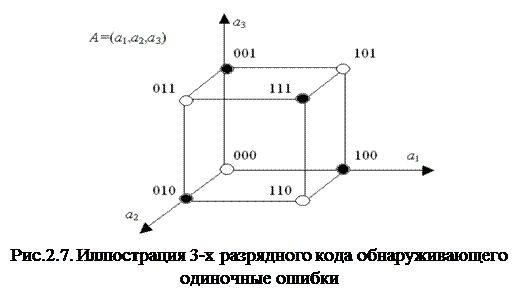
Пусть для 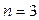(см. рис. 2.7) из всех возможных 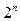кодовых комбинаций разрешены только комбинации 001, 010, 100 и 111. Тогда 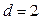, и искажение символа в одном из разрядов приведет к получению запрещенной кодовой комбинации 000, 011, 101 или 110, что легко выявляется при проверке. Таким образом, код 001, 010, 100, 111 обнаруживает ошибку в одном разряде (одиночную ошибку).

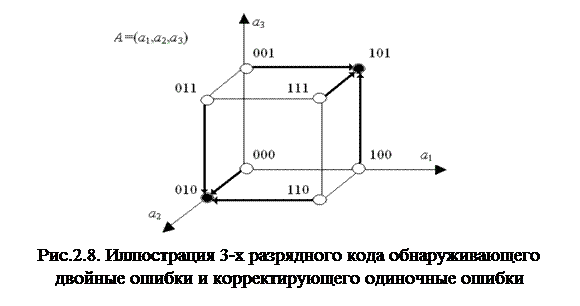
Легко построить код, обнаруживающий и двойные ошибки. Для этого в качестве разрешенных кодовых комбинаций необходимо выбрать наборы с 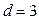, например наборы 010 и 101. При этом одиночные ошибки можно не только обнаруживать, но и исправлять. Действительно, получение запрещенных кодовых комбинаций 110, 000 или 011 указывает на наличие одиночной ошибки, для исправления которой необходимо перейти к ближайшей из разрешенных кодовых комбинаций – 010. Если же получены запрещенные кодовые комбинации 001,111 или 100, то для исправления одиночной ошибки необходимо перейти к ближайшей из разрешенных кодовых комбинаций - 101. Рассмотренный код и процесс исправления одиночных ошибок проиллюстрирован на рис.2.8.

Итак, построение помехозащищенных кодов связано с введением избыточности в передаваемые кодовые комбинации. При этом корректирующая способность кода, т.е. число обнаруживаемых и исправляемых ошибок, определяется главным образом кодовым расстоянием.

Простейшим из помехозащищенных кодов является код с проверкой на четность ( 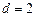). В этом коде к каждой комбинации 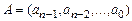добавляется один дополнительный проверочный разряд 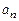, значение которого определяется следующим образом

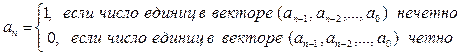
Таким образом, при отсутствии ошибок кодовая комбинация 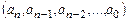всегда содержит четное число единиц. Если в результате проверки установлено, что кодовая комбинация 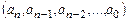содержит нечетное число единиц, то это указывает на наличие одиночной ошибки (или нечетного числа ошибок). Автоматическая коррекция ошибок в данном коде невозможна.

Аналогично можно построить код с проверкой на нечетность.

Подобные коды используются при организации последовательной передачи данных в глобальных сетях. Следует отметить, что в больших и мини-ЭВМ почти всегда используется проверка на четность. В персональных компьютерах проверка на четность практически не используется. С этим связана одна из распространенных ошибок среди неопытных пользователей. Они забывают при связи с компьютерными службами типа CompuServe переключать свои терминальные программы в режим использования 7 бит для данных и 1 бита для проверки на четность.