Примером двоичного кода является запись натурального числа 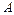 в позиционной системе счисления с основанием 2
в позиционной системе счисления с основанием 2
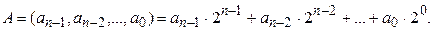
Пусть 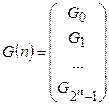 - последовательность двоичных кодовых слов длины
- последовательность двоичных кодовых слов длины 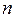 . Тогда рекурсивное определение последовательности кодовых слов в порядке двоичного счета будет следующее:
. Тогда рекурсивное определение последовательности кодовых слов в порядке двоичного счета будет следующее:
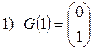
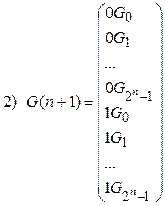
Наиболее прямым способом порождения данной последовательности кодовых слов является счет в системе счисления с основанием 2, что реализует алгоритм, представленный укрупненной блок-схемой на рис.2.2.
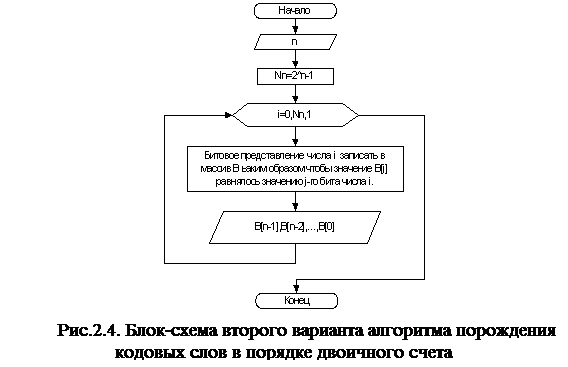
Укрупненная блок-схема показывает идеи алгоритма и не расскрывает многие детали реализации. В рассматриваемом алгоритме из укрупненной блок-схемы видно, что двоичные наборы длины n формируются в ячейках B[n-1],B[n-2],...,B[0], массива B. Ячейка B[n] массива B служит для организации завершения работы алгоритма. Ячейка B[n] принимает значение 1, когда все 2n наборов выданы. Также видно, что для реализации двоичного счета, т.е. для организации перехода от текущего кодового слова к следующему, используется простой прием:
· просматривается текущее кодовое слово в направлении от младшего разряда к старшему с целью поиска первого разряда, равного нулю (на укрупненной блок-схеме номер такого разряда сохраняется в переменной i);.
· найденному первому разряду, равному нулю, присваивается значение 1, а все «более младшие» разряды, значение которых равно 1, обнуляются.
 |
Однако из укрупненной блок схемы не видны детали реализации перехода от текущего кодового слова к следующему. Обычно подобная детализация не вызывает трудностей.
В некоторых случаях будем приводить детальные блок-схемы алгоритмов. Поскольку алгоритм порождения кодовых слов в порядке двоичного счета является первым рассматриваемым нами алгоритмом, то приведем его детальную блок-схему. Детальная блок-схема алгоритма представлена на рис. 2.3.
Еще один способ порождения последовательности кодовых слов в порядке двоичного счета заключается в переборе всех целых чисел от 0 до 2n-1 и обращением двоичного представления каждого из чисел в набор (bn-1,bn-2,...,b0). Обращение осуществляется с помощью битовых операций или с помощью операций целочисленного деления и получения остатка от деления.
Укрупненная блок схема алгоритма реализующего данный подход показана на рис.2.4.

Код Грэя
Другой пример последовательности двоичных кодовых слов - это код Грэя. Код Грэя обладает ценным свойством, заключающемся в том, что любые два соседних кодовых слова отличаются лишь значением в одном разряде (последовательность кодовых слов в порядке минимального изменения). Код Грэя используется при построении различных преобразователей аналог-код, где он позволяет свести к единице младшего разряда ошибку неоднозначности при считывании информации.
Рекурсивное определение двоично-отраженного кода Грея следующее (используются обозначения, введенные в разд.2.3.2):
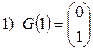
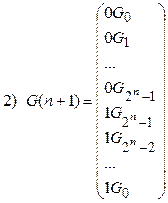
Примеры последовательностей двоичных наборов в порядке двоичного счета и порядке минимального изменения представлены в таблице 2.1.
| Таблица 2.1 | |||||
| Последовательности двоичных наборов в порядке двоичного счета и порядке минимального изменения | |||||
| Последовательности двоичных наборов в порядке двоичного счета | Последовательности двоичных наборов в порядке минимального изменения (коды Грэя) | ||||
| G(1) | G(2) | G(3) | G(1) | G(2) | G(3) |
Рассмотрим алгоритм порождения кода Грэя. Коды Грея удобно задавать начальным словом и последовательностью переходов, т.е. упорядоченным списком номеров разрядов (пронумерованных справа налево, нумерация с единицы), которые меняются при переходе от одного кодового слова к другому. Так для приведенного в таблице 2.1 кода G(3) начальное слово (000), а последовательность переходов будет иметь вид Т3=1,2,1,3,1,2,1.
Пусть 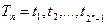 есть последовательность переходов для n-разрядного кода, тогда можно дать рекурсивное определение последовательности переходов.
есть последовательность переходов для n-разрядного кода, тогда можно дать рекурсивное определение последовательности переходов.
1) Т1=1,
2) 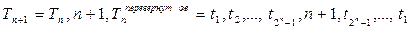 .
.
Следует отметить, что последовательности переходов Tn и 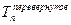 одинаковы. Поэтому данное рекурсивное определение упрощается:
одинаковы. Поэтому данное рекурсивное определение упрощается:
1) T1=1,
2) Tn+1=Tn,n+1,Tn.
Итак, для порождения кода Грея достаточно уметь порождать последовательность его переходов.
Последовательность переходов можно порождать итеративно, используя стек. Стек это один из видов организации хранения последовательности элементов данных. Элементы организуются по принципу «последний вошел - первый вышел». Более подробно стеки будут рассмотрены в разд.(2.4.5).
Вначале стек содержит элементы n,n-1,...,1 (с 1 в вершине, т.е. 1 вошла в стек последней). Затем верхний элемент стека - i извлекается из стека и помещается в последовательность переходов, после этого в стек добавляются элементы i-1,i-2,...,1. Процесс повторяется, пока стек не пуст. Алгоритм порождения кода Грея представлен укрупненной блок-схемой на рис.2.5.
 |
В укрупненной блок схеме не детализировано, как осуществлять операции работы со стеком. Отметим, что для организации стека S можно использовать массив и переменную t, следящую за вершиной стека. Пусть для S отведены ячейки S[1],S[2],...,S[m], и число элементов в стеке не превышает m, тогда пустой стек соответствует случаю t=0. Операции занесения в стек некоторого значения x и извлечения из стека будут осуществляться следующим образом:
· занесение x в стек S: t=t+1; S[t]=x;
· извлечение x из стека S: x:=S[t]; t:=t-1.
Также в укрупненной блок-схеме не детализировано, как выполнять инвертирование элемента q[i]. Заметим, что элемент имеет целочисленный тип, поэтому выполнение операции q[i]:=not q[i] не приведет к желаемому результату (объясните почему). Можно было реализовать операцию инвертирования, например следующим образом: q[i]:=q[i] xor 1 или q[i]:=not q[i] and 1 (объясните почему), но в данном случае лучше заменить инвертирование арифметическими операциями: q[i]:=1-q[i].
Оптимальное кодирование
До сих пор не учитывалось, что сообщения могут иметь различную вероятность появления. Пусть необходимо передать четыре сообщения A,B,C,D. Если их закодировать двоичным кодом, то получим четыре кодовых комбинации 00, 01, 10, 11. При равной вероятности каждого сообщения 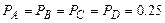 использование такого способа кодирования очевидно. Если же одно из сообщений встречается чаще других, то его следует кодировать более коротким словом, тогда как более редкие сообщения можно кодировать более длинным словом.
использование такого способа кодирования очевидно. Если же одно из сообщений встречается чаще других, то его следует кодировать более коротким словом, тогда как более редкие сообщения можно кодировать более длинным словом.
Один из способов построения оптимальных кодов заключается в следующем:
1. Сообщения разбиваются на две группы таким образом, чтобы сумма вероятностей в каждой группе была примерно одинакова. Одной группе приписывается символ 1, другой – 0.
Далее каждая из групп разбивается по такому же правилу, и вновь образовавшимся подгруппам также приписываются символы 1 и 0.
2. Разбиение (пункт 1) заканчивается тогда, когда в каждой подгруппе останется по одному сообщению. Совокупность символов, приписанных сообщениям в процессе разбиения, дает коды этих сообщений.
Пусть 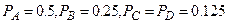 . Тогда процесс построения оптимального кода будет следующий:
. Тогда процесс построения оптимального кода будет следующий:
· после первого разбиения в первой группе останется единственное сообщение 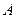 , во второй -
, во второй - 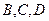 ;
;
· после второго разбиения в первой группе - 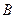 , во второй -
, во второй - 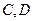 ;
;
· после третьего разбиения в первой группе - 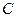 , во второй -
, во второй - 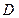 .
.
Третье разбиения будет последним, т.к. после него в каждой группе останется по одному сообщению. Данный процесс проиллюстрирован в таблице 2.2 и на рис.2.6.
| Таблица 2.2 | |||||
| Процесс построения оптимальных кодов | |||||
| Сообще-ние | Вероятность появления сообщения | Разбиения | Код сообщения | ||
| 1 | 2 | 3 | |||
| A | 0.5 | ||||
| B | 0.25 | ||||
| C | 0.125 | ||||
| D | 0.125 |
Используя формулу 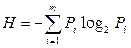 , найдем количество информации, приходящееся на одно сообщение (энтропию):
, найдем количество информации, приходящееся на одно сообщение (энтропию): 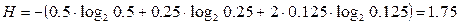 бит на сообщение.
бит на сообщение.
Среднюю длину кода, т.е. среднее число бит, приходящихся на одно сообщение, вычислим по формуле 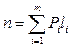 , где
, где 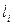 - число бит, требуемое для кодирования i-го сообщения. Для полученного оптимального кода имеем:
- число бит, требуемое для кодирования i-го сообщения. Для полученного оптимального кода имеем: 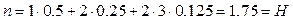 . При равномерном кодировании
. При равномерном кодировании 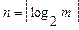 , в нашем случае (коды 00,01,10,11) :
, в нашем случае (коды 00,01,10,11) : 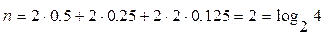 .
.
 |
При рассмотренном способе оптимального кодирования среднее число бит, приходящихся на одно сообщение находится в пределах от H до 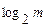 . Энтропия - это минимально возможное среднее число бит, которым может быть закодировано одно сообщение. В рассмотренном алгоритме построения оптимальных кодов n=H получается не всегда. Есть другие способы построения оптимальных кодов, позволяющие получить n=H, например, алгоритм арифметического кодирования.
. Энтропия - это минимально возможное среднее число бит, которым может быть закодировано одно сообщение. В рассмотренном алгоритме построения оптимальных кодов n=H получается не всегда. Есть другие способы построения оптимальных кодов, позволяющие получить n=H, например, алгоритм арифметического кодирования.
Дата: 2016-09-30, просмотров: 309.