Список сокращений
| 1НФ | Первая нормальная форма |
| 2НФ | Вторая нормальная форма |
| 3НФ | Третья нормальная форма |
| 4НФ | Четвертая нормальная форма |
| 5НФ | Пятая нормальная форма |
| АСВОК | Автоматизированная система ведения общесистемных классификаторов |
| АСУ | Автоматизированная система управления |
| АТД | Абстрактный тип данных |
| БД | База данных |
| ЕСКК | Единая система классификации и кодирования |
| ЖЦ | Жизненный цикл |
| ИПС | Информационно-поисковая система |
| ИС | Информационная система |
| ИСУ | Информационная система управления |
| ОК | Общесистемный классификатор |
| ПО | Программное обеспечение |
| СД | Структура данных |
| СЕИ | Составная единица информации |
| СОД | Система обработки данных |
| СППР | Система поддержки принятия решений |
| СУБД | Система управления базами данных |
| ЭИС | Экономическая информационная система |
Список сокращений. 1
1. ЭИС, их классификация и принципы построения. 5
1.1. Понятие системы.. 5
1.2. Понятие ЭИС. Назначение ЭИС.. 5
1.3.Классификация ЭИС.. 6
1.4. Основные принципы и методы построения ЭИС. 8
1.4.1. Принципы построения и функционирования ЭИС. 8
1.4.2.Структурный и объектно-ориентированный подходы к проектированию. 9
1.4.3.Понятие жизненного цикла ЭИС. 9
Вопросы для повторения. 10
Резюме по теме. 10
2.Теоретические основы работы с информацией. 10
2.1. Понятие информации. 11
2.2. Измерение количества информации. 12
2.3.Кодирование информации. 16
2.3.1.Оптимальное основание кода. 16
2.3.2.Запись натурального числа в двоичной системе. 17
2.3.3.Код Грэя. 20
2.3.4.Оптимальное кодирование. 22
2.3.5.Помехозащищенное кодирование. 24
2.4.Методы организации данных в памяти ЭВМ... 26
2.4.1.Типы данных, СД и АТД.. 26
2.4.2.Время выполнения программ.. 28
2.4.3.Списки. 29
2.4.4.Реализация списков. 30
2.4.5.Стеки. 34
2.4.6. Очереди. 35
2.4.7.Графы и деревья. 35
2.4.8.Некоторые СД для хранения графов и деревьев. 37
Вопросы для повторения. 43
Резюме по теме. 44
3. Особенности работы с экономической информацией. 44
3.1.Классификация и кодирование экономической информации. 44
3.2.Единая система классификации и кодирования. 48
3.3.Штриховое кодирование. 50
Вопросы для повторения. 55
Резюме по теме. 55
4.Модели данных. 55
4.1.Атрибуты, составные единицы информации, показатели, документы.. 55
4.2.Операции над СЕИ.. 57
4.3.Реляционная модель данных. 58
4.3.1. Отношения, как основа реляционной модели данных. 58
4.3.2. Операции над отношениями. 60
4.3.3. Нормализация отношений. 63
4.3.4. Функциональные зависимости. 64
4.3.5. Нормальные формы.. 65
Вопросы для повторения. 73
Резюме по теме. 74
5.Модели знаний. 74
5.1. Классификация знаний. 74
5.2. Продукционная модель представления знаний. 75
5.3.Представление знаний в виде семантической сети. 75
5.4. Фреймовая модель представления знаний. 76
5.5. Логическая (предикатная) модель представления знаний. 77
Вопросы для повторения. 77
Резюме по теме. 77
6.Моделирование предметных областей в экономике. 78
6.1.Понятие модели предметной области. 78
6.2.Структурная модель предметной области. 79
6.2.1.Функциональная методология IDEF0. 79
6.2.2. Функциональная методика потоков данных. 81
6.3.Объектная модель предметной области. 82
6.4. Сравнение методик моделирования предметной области. 83
Вопросы для повторения. 84
Резюме по теме. 84
Литература. 85
Рекомендуемая основная литература. 85
Рекомендуемая дополнительная литература. 85
Задачник. 86
Введение. 86
Краткое изложение используемых методов решения и основных теоретических положений 86
Примеры решения типовых задач. 86
Задачи для самостоятельного решения. 88
Практикум (лабораторный) 91
Лабораторная работа №1. Кодирование информации. 91
Требования к содержанию, оформлению и порядку выполнения. 91
Теоретическая часть. 91
Общая постановка задачи. 91
Список индивидуальных данных. 93
Пример выполнения работы.. 93
Контрольные вопросы к защите. 97
Способ оценки результатов. 98
Лабораторная работа №2. Реализация абстрактных типов данных. 98
Требования к содержанию, оформлению и порядку выполнения. 98
Теоретическая часть. 98
Общая постановка задачи. 99
Список индивидуальных данных. 99
Пример выполнения работы.. 99
Контрольные вопросы к защите. 102
Способ оценки результатов. 102
Лабораторная работа №3. СД для хранения графов. 102
Требования к содержанию, оформлению и порядку выполнения. 102
Теоретическая часть. 102
Общая постановка задачи. 102
Список индивидуальных данных. 103
Пример выполнения работы.. 104
Контрольные вопросы к защите. 105
Способ оценки результатов. 106
Лабораторная работа №4. Технологии штрихового кодирования. 106
Требования к содержанию, оформлению и порядку выполнения. 106
Теоретическая часть. 106
Общая постановка задачи. 106
Список индивидуальных данных. 107
Пример выполнения работы.. 107
Контрольные вопросы к защите. 108
Способ оценки результатов. 109
Лабораторная работа №5. Нормализация отношений. 109
Требования к содержанию, оформлению и порядку выполнения. 109
Теоретическая часть. 109
Общая постановка задачи. 109
Список индивидуальных данных. 109
Пример выполнения работы.. 110
Контрольные вопросы к защите. 112
Способ оценки результатов. 112
ЭИС, их классификация и принципы построения
Цели и задачи изучения темы
Целью темы является изучение понятий системы и экономической информационной системы (ЭИС), классов ЭИС и основных принципов и методов их построения .
Понятие системы
Систему понимают как комплекс взаимосвязанных элементов, действующих как единое целое. Любая система определяется следующими компонентами:
1.Структура - множество элементов системы и их взаимосвязей.
2.Входы и выходы - материальные потоки или потоки сообщений, поступающих в систему или выводимые ею. Входной поток - набор параметров {xi}, значения этих параметров по всем входным потокам образуют вектор-функцию Х. В простейшем случае X=f(t), чаще на практике X=j(X(t),t), где t - время. Функция выхода Y определяется аналогично.
3.Закон поведения системы - функция Y=F(X).
4.Цель и ограничения. Процесс функционирования системы описывается набором переменных u1,u2,...,uN. Часть из них должна поддерживаться в экстремальном значении. Обычно в экстремальном значении должна поддерживаться одна переменная, например, максимум u1. В этом случае функция u1=f(X,Y,u2,u3,...,uN) - целевая функция. Она определяет соответствие цели результатам функционирования системы. Часто целевая функция не имеет аналитического выражения. На остальные переменные могут быть наложены ограничения.
К основным свойствам систем относят следующие свойства:
1.Относительность - состав элементов, взаимосвязей, входов, выходов, целей, ограничений зависит от целей исследователя.
2.Делимость - систему можно представить состоящей из относительно самостоятельных частей (подсистем), каждая из которых рассматривается как система. Такое деление называют декомпозицией системы. Декомпозиция упрощает анализ системы. Деление системы на подсистемы условно.
3.Целостность - согласованность цели функционирования всей системы с целями функционирования ее подсистем и элементов.
Понятие ЭИС. Назначение ЭИС
ЭИС - система, функционирование которой во времени заключается в сборе, хранении, обработке и распространении экономической информации, т.е. информации о деятельности какого-либо экономического объекта реального мира.
Назначение ЭИС:
1.Решение задач обработки данных - обработка и хранение экономической информации с целью выдачи сводной информации для управления экономическим объектом.
2.Автоматизация конторских работ - ведение картотек, обработка текстовой информации, машинная графика, электронная почта и связь.
3.Задачи, основанные на методах искусственного интеллекта - для принятия управленческих решений.
Классификация ЭИС
ЭИС по назначению классифицируются следующим образом:
1.Управляющие информационные системы (ИС). Данные системы предназначены для управления технологическими процессами на предприятии.
2.Системы административно-организационного типа для обслуживания коллектива специалистов, управляющих предприятием.
Также распространена классификация ЭИС по функциональному признаку:
1.Системы обработки данных (СОД). СОД (рис.1.1) производит информационное обслуживание специалистов органа управления объектом, принимающих управленческие решения. Решение, принятое на основе предоставленной информации, передается на управляемый объект, минуя СОД. Информация от управляемого объекта может поступать к органу управления и непосредственно.
 |
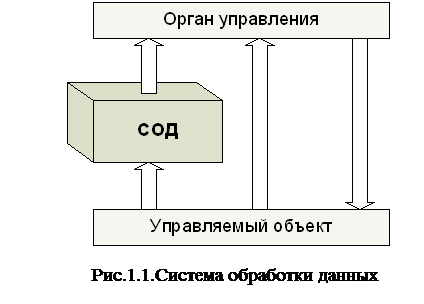2.Автоматизированные системы управления (АСУ). АСУ (рис.1.2) отличается от СОД тем, что они способны выполнять выбор управленческих решений. Иногда аналогичные системы называют информационными системами управления (ИСУ) и системами поддержки принятия решений (СППР). Разница между ИСУ и СППР заключается в уровне управления. ИСУ ориентированы на тактический уровень управления. СППР в основном используются для стратегического долгосрочного управления.
3. Информационно-поисковые системы (ИПС) - системы, предназначенные для поиска требуемых документов, т.е. документов, удовлетворяющих заданному условию.
 |
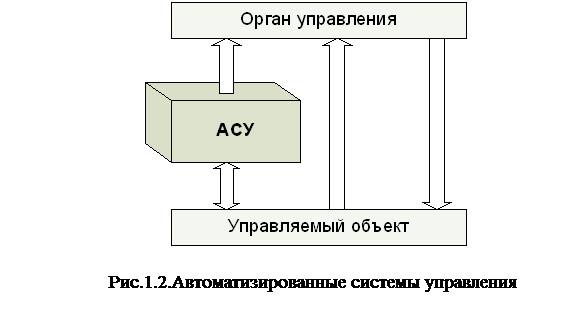Применяются и другие классификации ЭИС. По режиму работы ЭИС классифицируются следующим образом:
1.ЭИС, использующие пакетный режим работы. При пакетном режиме данные в системе накапливаются до тех пор, пока не наступит заданный момент времени или объем данных не превысит некоторый предел. Затем имеющаяся информация обрабатывается несколькими последовательно запускаемыми программами. Пример такого режима - сбор и группировка статистической отчетности предприятия.
2.ЭИС, использующие диалоговый режим работы. Диалоговый режим предоставляет возможность обмена сообщениями между пользователем и системой.
По способу распределения вычислительных ресурсов различают:
1.Локальные ЭИС. Локальная система использует один компьютер.
2.Распределенные ЭИС. Распределенная система представляет собой объединение ИС, каждая из которых реализована, как правило, на отдельном компьютере и выполняет собственные, не зависимые от других систем функции. Основная цель создания таких систем - коллективное использование информационных фондов и вычислительных ресурсов. Отдельные ИС, как правило, территориально удалены друг от друга.
Рассмотренные классификации ЭИС проиллюстрированы на рис.1.3.
 |
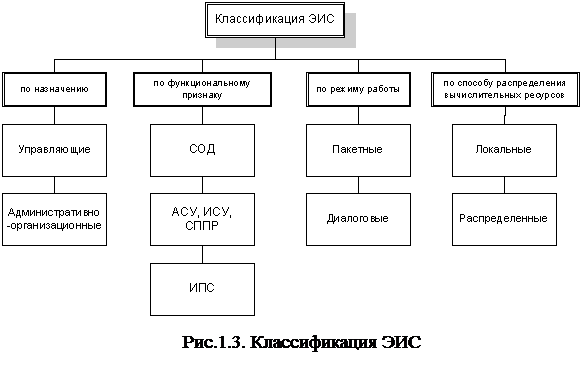Вопросы для повторения
1. Понятие системы.
2. Компоненты системы.
3. Основные свойства систем.
4. Понятие ЭИС.
5. Назначение ЭИС.
6. Классификация ЭИС по назначению.
7. Классификация ЭИС по функциональному признаку.
8. Классификация ЭИС по режиму работы.
9. Классификация ЭИС по способу распределения вычислительных ресурсов.
10. Основные принципы построения и функционирования ЭИС.
11. Принцип иерархической декомпозиции.
12. Требования к «правильной» декомпозиции.
13. Сущность структурного подхода к проектированию ЭИС.
14. Сущность объектно-ориентированного подхода к проектированию ЭИС.
15. Понятие ЖЦ ЭИС.
Резюме по теме
Дано понятие ЭИС. Рассмотрены основные способы классификации и принципы построения таких систем.
Цели и задачи изучения темы
В данной теме рассматриваются основы теории информации и некоторые методы организации данных в памяти ЭВМ. Целями темы являются:
· освоение основных понятий теории информации;
· освоение понятий кодирования информации и ознакомление с некоторыми видами кодов;
· освоение некоторых способов представления данных в памяти ЭВМ.
Понятие информации
В широком смысле невозможно дать одно точное определение информации. С одной стороны, информация может рассматриваться как ресурс (аналогично трудовым, материальным и т.д.). Информация в этом смысле - новые сведения, позволяющие улучшить процессы, связанные с преобразованием вещества, энергии и самой информации. С другой стороны, информация неотделима от процесса информирования, где есть источник и потребитель информации: здесь информация - сведения, расширяющие запас знаний конечного потребителя.
Различают три фазы существования информации:
1.Ассимилированная информация - представление сообщений в сознании человека, наложенное на его систему понятий и оценок.
2.Документированная информация - сведения, зафиксированные в знаковой форме на каком-то физическом носителе.
3.Передаваемая информация - сведения, рассматриваемые в момент передачи информации от источника к приемнику.
В дальнейшем будем рассматривать фазы 2 и 3.
Основная масса информации собирается, передается и обрабатывается с помощью знаков. Знаки это сигналы, которые могут передавать информацию при наличии соглашения об их смысловом содержании между источником и приемником информации. Набор знаков, для которых существует указанное соглашение, называется знаковой системой.
Информация на пути от источника к потребителю проходит через ряд преобразователей - кодирующие и декодирующие устройства, ЭВМ и т.д. Смысловые свойства сообщений при этом отступают на второй план, и понятие «информация» заменяется общим понятием «данные». Данные - набор утверждений, фактов и (или) цифр, логически связанных между собой.
Экономическая информация - информация об экономических процессах (производстве, распределении, обмене и потреблении материальных благ). Для ее обработки характерны сравнительно простые алгоритмы (упорядочение, выборка, корректировка).
Экономическая информация классифицируется по следующим признакам:
1.По отношению к системе - входная, выходная, внутренняя информация.
2.По признаку времени:
· перспективная (прогнозная) информация;
· ретроспективная (учетная) информация;
· периодические сообщения;
· непериодические сообщения.
3.По функциональным признакам (по функциональным подсистемам экономического объекта, например, о трудовых ресурсах, финансах, планирование, нормирование, учет и т.д.).
Кодирование информации
Преобразование сообщения в код называют кодированием информации. Такое преобразование осуществляется по определенному правилу (алгоритму). Множество различных кодовых комбинаций, получают при данном правиле кодирования, называют кодом.
Оптимальное основание кода
Важными характеристиками кода являются основание (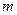 
) и длина ( 
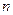) кода. Под основанием кода понимается число возможных значений, которые могут принимать элементы (символы, буквы) кодовой комбинации (слова), а под длиной - число элементов в этой комбинации.
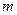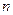Например для кодирования сигнала, уровень которого изменяется от 0 до 10 В, с погрешностью 10 мВ можно предложить различные варианты выбора и : 1) 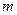=1000, 
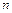=1; 2) 
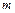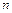=2, =10 (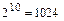 
) и т.д.
Для определения оптимальных значени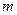й и 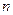воспользуемся критерием минимума произведения 
.
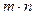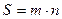
Как было отмечено ране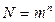е 
, где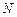 
- заданное число сообщений (число различных комбинаций сигнала). Логарифмируя, получим
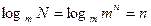
Следовательно,
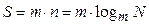
Используя формулу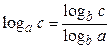 
, получим
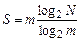
Условие минимума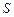 
примет вид:
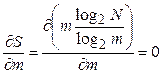
Воспользовавшись тождествами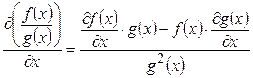 
, 
, 
, 
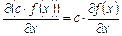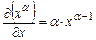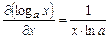, получим
.
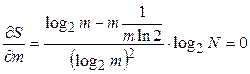Далее, используя тождество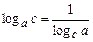 
, окончательно получим
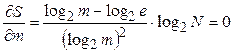
Из последнего тождества следует, что оптимальное значение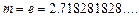 
Т.к. 
должно быть целое, то оптимальным значением 
является 3 или 2. На практике чаще используется основание кода 
.
Код Грэя
Другой пример последовательности двоичных кодовых слов - это код Грэя. Код Грэя обладает ценным свойством, заключающемся в том, что любые два соседних кодовых слова отличаются лишь значением в одном разряде (последовательность кодовых слов в порядке минимального изменения). Код Грэя используется при построении различных преобразователей аналог-код, где он позволяет свести к единице младшего разряда ошибку неоднозначности при считывании информации.
Рекурсивное определение двоично-отраженного кода Грея следующее (используются обозначения, введенные в разд.2.3.2):
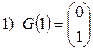
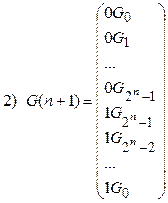
Примеры последовательностей двоичных наборов в порядке двоичного счета и порядке минимального изменения представлены в таблице 2.1.
| Таблица 2.1 | |||||
| Последовательности двоичных наборов в порядке двоичного счета и порядке минимального изменения | |||||
| Последовательности двоичных наборов в порядке двоичного счета | Последовательности двоичных наборов в порядке минимального изменения (коды Грэя) | ||||
| G(1) | G(2) | G(3) | G(1) | G(2) | G(3) |
Рассмотрим алгоритм порождения кода Грэя. Коды Грея удобно задавать начальным словом и последовательностью переходов, т.е. упорядоченным списком номеров разрядов (пронумерованных справа налево, нумерация с единицы), которые меняются при переходе от одного кодового слова к другому. Так для приведенного в таблице 2.1 кода G(3) начальное слово (000), а последовательность переходов будет иметь вид Т3=1,2,1,3,1,2,1.
Пусть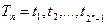 
есть последовательность переходов для n-разрядного кода, тогда можно дать рекурсивное определение последовательности переходов.
1) Т1=1,
2) 
.
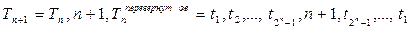Следует отметить, что последовательности переходов Tn и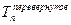 
одинаковы. Поэтому данное рекурсивное определение упрощается:
1) T1=1,
2) Tn+1=Tn,n+1,Tn.
Итак, для порождения кода Грея достаточно уметь порождать последовательность его переходов.
Последовательность переходов можно порождать итеративно, используя стек. Стек это один из видов организации хранения последовательности элементов данных. Элементы организуются по принципу «последний вошел - первый вышел». Более подробно стеки будут рассмотрены в разд.(2.4.5).
Вначале стек содержит элементы n,n-1,...,1 (с 1 в вершине, т.е. 1 вошла в стек последней). Затем верхний элемент стека - i извлекается из стека и помещается в последовательность переходов, после этого в стек добавляются элементы i-1,i-2,...,1. Процесс повторяется, пока стек не пуст. Алгоритм порождения кода Грея представлен укрупненной блок-схемой на рис.2.5.
 |
В укрупненной блок схеме не детализировано, как осуществлять операции работы со стеком. Отметим, что для организации стека S можно использовать массив и переменную t, следящую за вершиной стека. Пусть для S отведены ячейки S[1],S[2],...,S[m], и число элементов в стеке не превышает m, тогда пустой стек соответствует случаю t=0. Операции занесения в стек некоторого значения x и извлечения из стека будут осуществляться следующим образом:
· занесение x в стек S: t=t+1; S[t]=x;
· извлечение x из стека S: x:=S[t]; t:=t-1.
Также в укрупненной блок-схеме не детализировано, как выполнять инвертирование элемента q[i]. Заметим, что элемент имеет целочисленный тип, поэтому выполнение операции q[i]:=not q[i] не приведет к желаемому результату (объясните почему). Можно было реализовать операцию инвертирования, например следующим образом: q[i]:=q[i] xor 1 или q[i]:=not q[i] and 1 (объясните почему), но в данном случае лучше заменить инвертирование арифметическими операциями: q[i]:=1-q[i].
Оптимальное кодирование
До сих пор не учитывалось, что сообщения могут иметь различную вероятность появления. Пусть необходимо передать четыре сообщения A,B,C,D. Если их закодировать двоичным кодом, то получим четыре кодовых комбинации 00, 01, 10, 11. При равной вероятности каждого сообщения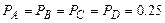 
использование такого способа кодирования очевидно. Если же одно из сообщений встречается чаще других, то его следует кодировать более коротким словом, тогда как более редкие сообщения можно кодировать более длинным словом.
Один из способов построения оптимальных кодов заключается в следующем:
1. Сообщения разбиваются на две группы таким образом, чтобы сумма вероятностей в каждой группе была примерно одинакова. Одной группе приписывается символ 1, другой – 0.
Далее каждая из групп разбивается по такому же правилу, и вновь образовавшимся подгруппам также приписываются символы 1 и 0.
2. Разбиение (пункт 1) заканчивается тогда, когда в каждой подгруппе останется по одному сообщению. Совокупность символов, приписанных сообщениям в процессе разбиения, дает коды этих сообщений.
Пусть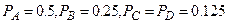 
. Тогда процесс построения оптимального кода будет следующий:
· после первого разбиения в первой группе останется единственное сообщение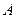 
, во второй - 
;
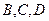· после второго разбиения в первой группе -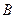 
, во второй - 
;
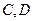· после третьего разбиения в первой группе -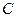 
, во второй - 
.
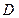Третье разбиения будет последним, т.к. после него в каждой группе останется по одному сообщению. Данный процесс проиллюстрирован в таблице 2.2 и на рис.2.6.
| Таблица 2.2 | |||||
| Процесс построения оптимальных кодов | |||||
| Сообще-ние | Вероятность появления сообщения | Разбиения | Код сообщения | ||
| 1 | 2 | 3 | |||
| A | 0.5 | ||||
| B | 0.25 | ||||
| C | 0.125 | ||||
| D | 0.125 |
Используя формулу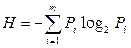 
, найдем количество информации, приходящееся на одно сообщение (энтропию): 
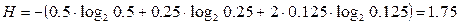бит на сообщение.
Среднюю длину кода, т.е. среднее число бит, приходящихся на одно сообщение, вычислим по формул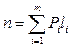е 
, где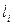 
- число бит, требуемое для кодирования i-го сообщения. Для полученного оптимального кода имеем: 
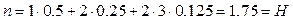. При равномерном кодировании 
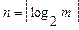, в нашем случае (коды 00,01,10,11) : 
.
 |
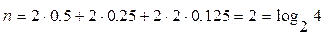При рассмотренном способе оптимального кодирования среднее число бит, приходящихся на одно сообщение находится в пределах от H до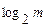 
. Энтропия - это минимально возможное среднее число бит, которым может быть закодировано одно сообщение. В рассмотренном алгоритме построения оптимальных кодов n=H получается не всегда. Есть другие способы построения оптимальных кодов, позволяющие получить n=H, например, алгоритм арифметического кодирования.
Типы данных, СД и АТД
Тип данных - это множество значений, которые может принимать переменная, и множество операций, которые можно выполнять над этими переменными. Набор базовых типов данных отличается в различных языках.
Абстрактный тип данных (АТД) - это математическая модель плюс различные операторы, определенные в рамках этой модели.
Для представления АТД используются структуры данных (СД), которые представляют собой набор переменных, возможно, различных типов данных, объединенных определенным образом.
Базовым строительным блоком СД является ячейка, которая предназначена для хранения значения определенного базового или составного типа данных. СД создаются путем задания имен совокупностям (агрегатам) ячеек и интерпретации значения некоторых ячеек как указателей на другие ячейки.
В качестве простейшего механизма агрегирования ячеек в большинстве языков программирования можно применять (одномерный) массив, т.е. последовательность ячеек определенного типа.
Другим общим механизмом агрегирования ячеек в языках программирования является структура (запись). Запись можно рассматривать как ячейку, состоящую из нескольких других ячеек (называемых полями), значения в которых могут быть разных типов.
Массивы и записи являются структурами с произвольным доступом, подразумевая под этим, что время доступа к компонентам массива или записи не зависит от значения индекса массива или указателя поля записи.
Третий метод агрегирования ячеек, который можно найти в языках программирования, это файл. Файл, как и одномерный массив, является последовательностью значений определенного типа. Различают файлы прямого и последовательного доступа. В файле прямого доступа имеется индекс, т.е. все ячейки (компоненты) файла пронумерованы. Доступ может быть осуществлен к любой ячейке. Файл последовательного доступа не имеет индексов: его элементы доступны только в том порядке, в каком они были записаны в файл.
Достоинство агрегирования с помощью файла заключается в том, что файл не имеет ограничения на количество составляющих его элементов, и это количество может изменяться во время выполнения программы.
В дополнение к средствам агрегирования ячеек в языках программирования можно использовать указатели и курсоры. Указатель - это ячейка, чье значение указывает на другую ячейку. При графическом представлении СД в виде схемы тот факт, что ячейка А является указателем на ячейку В, показывается с помощью стрелки от ячейки А к ячейке В.
Курсор - это ячейка с целочисленным значением, используемая для указания на массив. В качестве способа указания курсор работает так же, как и указатель, но курсор можно использовать и в языках, которые не имеют явного типа указателя.
В схемах структур данных принято рисовать стрелку из ячейки курсора к ячейке, на которую указывает курсор. Иногда также указывают целое число в ячейке курсора, напоминая тем самым, что это ненастоящий указатель.
Пример СД представлен на рис.2.9.
 |
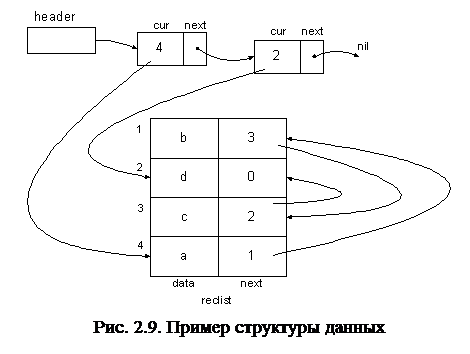В данной структуре ячейка header содержит указатель на запись, состоящую из двух полей: cur и next. Поле cur содержит курсор, содержащий индекс логически первого элемента массива reclist (в данном случае четвертый элемент массива является логически первым). Поле next содержит указатель на аналогичную запись, в которой поле cur содержит курсор на логически последнюю запись массива reclist (в примере это вторая запись), а поле next содержит пустой указатель. Массив reclist состоит из четырех записей с индексами от 1 до 4. Каждая запись состоит из двух полей: data и next. Поле data содержит данные (в примере это символы a,b,c,d). Логический порядок элементов массива определяется значением курсора в поле next - курсор хранит индекс логически следующего элемента массива. Так за четвертым элементом следует первый, за первым - третий, за третьим - второй. Второй элемент массива логически последний, т.к. значение поля next второго элемента равно 0, т.е. отличается от любого значения индекса массива - 1,2,3 или 4.
Время выполнения программ
В зависимости от выбранных структур данных может меняться время выполнения программ. В данном курсе, как правило, приводятся временные оценки алгоритмов без доказательства. Рассмотрим общепринятые временные оценки алгоритмов.
Время выполнения программы обычно определяют как функцию от длины исходных данных. Обычно говорят, что время выполнения программы выражается функцией T(n) от входных данных размера n.
Для многих программ время выполнения является функцией входных данных, а не их размера. В этом случае T(n) определяется как функция времени выполнения программы в наихудшем случае, т.е. как максимум времени выполнения по всем входным данным размера n. Также иногда рассматривают Tср(n) как среднее время выполнения по всем входным данным размера n. На практике среднее время найти сложнее, чем наихудшее.
Считается, что все функции времени определены на множестве неотрицательных целых чисел, и их значения также неотрицательны, но необязательно целые.
Для описания скорости роста функций времени выполнения программ используется O-символика. Например, когда говорят, что время выполнения T(n) некоторой программы имеет порядок O(n2) (читается «о-большое от n в квадрате» или «о от n в квадрате»), то подразумевают, что существуют положительные константы c и n0 такие, что для всех n³n0 выполняется неравенство T(n)£ T¢(n), где T¢(n)=c×n2.
Пример. Пусть T1(n)=(n+5)2. Тогда T1(n) будет иметь порядок O(n2). Действительно, если положить n0=1 и c=37, то легко показать, что для n³1 будет выполняться неравенство (n+5)2£T2(n), T2(n)=36×n2.
В общем случае будем говорить, что T(n) имеет порядок O(f(n)), если существуют положительные константы c и n0 такие, что для всех n³n0 выполняется неравенство T(n)£c×f(n).
Пример. Пусть T3(n)=3×n3+2×n2. Данная функция имеет порядок O(n3). Действительно, если положить n0=0 и c=5, то легко показать, что для n³0 будет выполняться неравенство 3×n3+2×n2£5×n3. Можно сказать, что T3(n)=3×n3+2×n2 имеет порядок O(n4), но это более слабое утверждение, чем то, что T3(n)=3×n3+2×n2 имеет порядок O(n3).
Применение O-символики для оценок времени выполнения алгоритмов чаще предпочтительнее, чем использование конкретных функций времени. Однако, для оценки реальных программ, т.е. программ работающих с данными ограниченного размера, нужно учитывать вид конкретных функций времени.
Пример. Пусть одна и та же задача может быть решена с помощью двух программ P1, P2 или P3, имеющих функции времени T1(n)=(n+5)2, T2(n)=36×n2, T3(n)=3×n3+2×n2 соответственно. Значения данных функций для различных значений n сведены в табл.2.3. Из таблицы видно, что функция T3(n) для n=1 и n=2 имеет меньшее значение, чем функция T1(n). Поэтому, несмотря на то, что функция T3(n) имеет порядок O(n3), а функция T1(n) - O(n2), использование программы P3 при n=1 и n=2 более предпочтительно, чем использование программы P1. Также функция T3(n) для n=1,2,…,11 имеет меньшее значение, чем функция T2(n). Поэтому для n=1,2,…,11 предпочтительнее использовать программу PЗ, чем программу P2, несмотря на то, что порядок функции T3(n) - O(n3), а функция T2(n) - O(n2).
| Таблица 2.3 | |||||||
| Значения функций времени выполнения программ | |||||||
| n | T1(n)= (n+5)2 | T2(n)= 36×n2 | T3(n)= 3×n3+2×n2 | n | T1(n)= (n+5)2 | T2(n)= 36×n2 | T3(n)= 3×n3+2×n2 |
Списки
Список представляет собой последовательность элементов определенного типа. Список представляется в виде последовательности элементов, разделенных запятыми: a1,a2,...,an, где n³0, и все ai имеют некоторый тип elementtype. Количество элементов n называют длиной списка. Если n³1, то a1 называется первым элементом, а an - последним элементом списка. В случае n=0 имеем пустой список, который не содержит элементов.
Важное свойство списка заключается в том, что его элементы можно линейно упорядочить в соответствии с их позицией в списке. Говорят, что элемент ai предшествует ai+1 для i=1,2,...,n-1 и ai следует за ai-1 для i = 2,3,...,n. Также говорят, что элемент ai имеет позицию i.
Определим множества операторов списка. При этом будем использовать следующие обозначения: L - список объектов типа elementtype, x - объект типа elementtype, р - позиция элемента в списке. Обычно позиции - это целые положительные числа, но на практике могут встретиться другие представления.
1. INSERT(x,p,L). Этот оператор вставляет объект x в позицию p в списке L, перемещая элементы от позиции p и далее в следующую, более высокую позицию. Таким образом, если список L состоит из элементов a1,a2,...,an, то после выполнения этого оператора он будет имет
Дата: 2016-09-30, просмотров: 172.
