Информация передается с помощью некоторых сигналов. Сигналы могут быть самые разные: световые, голосовые, электрические и т.д. К сигналам также относятся книги, письма и т.п. В общем случае под сигналом понимают физический процесс, однозначно отображающий передаваемое сообщение с заданной точностью, пригодный для обработки и передачи сообщения на расстояние.

Рассмотрим процесс перехода от непрерывного сигнала к близкому дискретному сигналу. Такой процесс называют дискретизацией сигнала. Устройство, осуществляющее переход от непрерывных (аналоговых) сигналов к дискретным (цифровым) сигналам называют аналого-цифровым преобразователем.

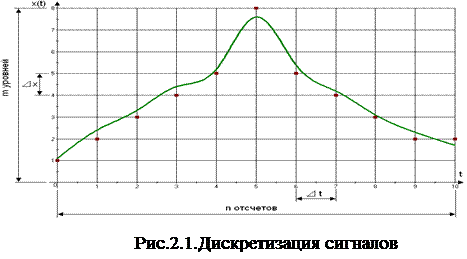
Пример дискретного сигнала – последовательность импульсов с изменяющейся амплитудой. Процесс дискретизации состоит из двух этапов (см. рис.2.1):

1.Дискретизация по времени.

2.Дискретизация по уровню.

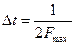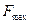При выборе частоты дискретизации по времени используют теорему В.А. Котельникова, согласно которой всякий непрерывный сигнал, имеющий ограниченный частотный спектр, полностью определяется своими дискретными значениями в моменты отсчета, отстоящие друг от друга на интервал , где - максимальная частота в спектре сигнала. Другими словами дискретизация по времени не приводит к потере информации, если частота дискретизации 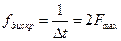в два раза выше .

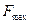Однако, допущение об ограниченности частотного спектра для реальных сигналов, как правило, не выполняется. Поэтому на практике частоту дискретизации выбирают следующим образом: 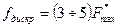, а 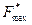выбирают так, чтобы в диапазоне частот 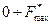содержалось не менее 90% средней мощности сигнала.

Если сигнал имеет конечную длительность 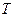, то число его дискретных отсчетов во времени можно оценить с помощью теоремы Котельникова 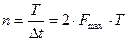. Число уровней сигнала определяется как .

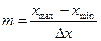Количество информации, которое можно перенести сигналом, будет тем больше, чем больше число комбинаций сигнала (сообщений).

Для подсчета числа таких комбинаций в нашем случае воспользуемся аксиомой комбинаторики – правилом произведения.

Правило произведения. Если некоторый выбор A можно осуществить 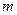способами, а для каждого из этих способов некоторый другой выбор B можно осуществить 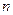способами, то выбор «A и B» в указанном порядке можно осуществить 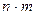способами. Это правило можно обобщить для произвольного числа выборов.

В нашем случае в каждый дискретный момент времени сигнал может принимать одно из 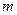значений. Т.е. в первый момент времени можно выбрать любой из 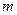возможных уровней сигнала, во второй момент времени можно выбрать любой из 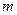возможных уровней сигнала и так далее. Всего моментов времени 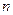, следовательно, по правилу произведения число возможных комбинаций сигнала или число возможных сообщений выражается формулой

.

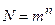Число 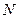дает комбинаторную оценку информации, содержащейся в произвольном дискретном сообщении (слове) из 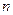элементов (букв), каждая из которых принимает одно из 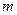возможных значений, составляющих некоторый алфавит.

В качестве меры количества информации принято использовать логарифм числа возможных сообщений

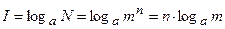
Таким образом, количество информации в сигнале пропорционально длительности сигнала (числу отсчетов 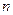). Выбор основания логарифма 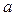определяет единицу измерения количества информации. Если 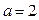, то 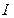измеряется в битах. Один бит – это количество информации, соответствующее одному из двух равновозможных сообщений типа «да» или «нет» (0 или 1). Таким образом

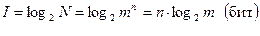(1)

Бит является наименьшей единицей измерения информации. Кроме того, в ЭВМ в качестве единицы измерения информации используется байт (Б). Байт представляет собой вектор, состоящий из 8 бит. Очевидно, что байтом можно закодировать 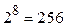различных сообщений. Также широко используются килобайт (КБ), 1КБ= 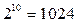Б и мегабайт (МБ), 1М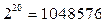Б= Б.

Основы количественной оценки информации были заложены Н.Виннером и К.Шенноном в 1948 году.

Далее попытаемся ответить на вопрос - сколько бит информации приходится на одну букву русского языка?

В русском языке 33 буквы. Однако, буквы «е» и «ё» принято ститать за одну букву. Также за одну букву можно считать твердый и мягкий знаки. А промежуток между словами (пробел), наоборот, следует считать за букву. В итоге, в русском языке имеется 32 кодовых знака. Тогда информация, приходящаяся на одну букву, будет равна 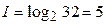бит.

Это максимальная информация, приходящаяся на букву. Однако буквы в тексте встречаются с различной частотой. Например, относительная частота пробела равна 0.175. Это означает, что на 1000 букв текста в среднем приходится 175 пробелов. Относительная частота буквы «о» равна 0.09, буквы «а» – 0.062, буквы «щ» – 0.003 и т.д. Используемый термин «частота появления» обычно заменяют на термин «вероятность».

Отметим, что различная частота появления букв (вероятность) в текстах ложится в основу построения некоторых систем сжатия информации (архиваторов). Принцип работы таких систем основан на том, что для кодирования частовстречающихся букв используются короткие кодовые слова, а для кодирования редковстречающихся букв используются более длинные слова.

Из-за того, что буквы неравновероятны, информация, которую несет одна буква, уменьшается с 5 бит до 4.35 бита. Но и эта оценка завышена. Дело в том, что здесь информация вычисляется в предположении, что рассматривается одна изолированная буква текста, а предыдущие буквы неизвестны. На самом деле это не так. Действительно, если Вы прочитали слово «котор...», то следующей буквой может быть лишь «а», «ы», «о» или «у», т.о. выбор делается из 4 букв, а не из 32. В результате получается, что с учетом текстовых и стилистических связей, информация, реально приходящаяся на букву равна 0.5-1.5 бита.

Для оценки информативности текстов используют понятие избыточности текста. Пусть текст состоит из 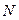букв и содержит 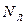лишних букв, тогда избыточность текста вычисляется следующим образом:

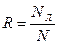
Реальная информация, приходящаяся на букву, вычисляется следующим образом .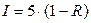

Шеннон предложил следующий способ подсчета избыточности текста: прочитываете 10-20 слов текста, при этом последующая часть текста должна быть закрыта, далее пытаетесь угадать с одной попытки первую закрытую букву, затем открываете эту букву и угадываете следующую и т.д. Опыт производится на 100-200 буквах текста. Отношение числа угаданных букв к общему числу угадываемых букв дает приближенное значение избыточности текста 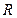. Чем продолжительнее опыт, тем точнее результат.

Примером языка, лишенного избыточности, является язык цифр.

Все рассуждения о количестве информации в текстах относятся и к произвольным сигналам. В формуле (1) не учитывалось, что различные значения (уровни) дискретного сигнала могут появляться с различными вероятностями.

Пусть 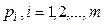- вероятности появления 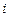-го значения сигнала ( 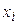). Пусть также 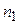отсчетов сигнал принимает значение 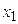, 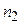отсчетов - значение 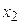и т.д. Вероятность появления такого сигнала определяется следующим образом

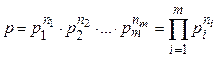
Если общее число отсчетов 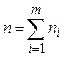достаточно велико, то можно положить 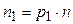, ,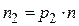..., . 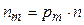Тогда

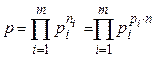
При достаточно большом числе отсчетов ( 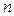) можно считать, что все возможные комбинации сигнала ( 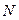) равновероятны, т.е. 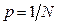, следовательно

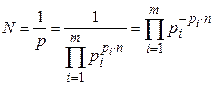
Логарифмируя, найдем количество информации в сигнале

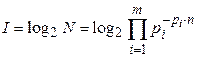
Используя тождества 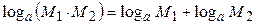и 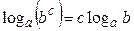, окончательно получим

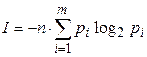(2)

Если все значения сигнала равновероятны ( 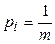), то формулы (1) и (2) совпадают .

Если сигнал принимает какое-либо значение 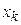с вероятностью, равной единице ( 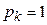), то для 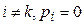и в соответствии с формулой (2) получим .

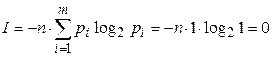Количество информации, приходящееся на один отсчет сигнала, называют удельной информативностью или энтропией сигнала.

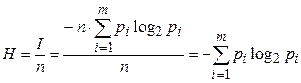
Энтропия является мерой неопределенности исследуемого процесса.

Кодирование информации

Преобразование сообщения в код называют кодированием информации. Такое преобразование осуществляется по определенному правилу (алгоритму). Множество различных кодовых комбинаций, получают при данном правиле кодирования, называют кодом.

Оптимальное основание кода

Важными характеристиками кода являются основание ( 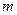) и длина ( 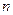) кода. Под основанием кода понимается число возможных значений, которые могут принимать элементы (символы, буквы) кодовой комбинации (слова), а под длиной - число элементов в этой комбинации.

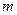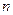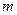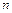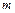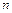Например для кодирования сигнала, уровень которого изменяется от 0 до 10 В, с погрешностью 10 мВ можно предложить различные варианты выбора и : 1) =1000, =1; 2) =2, =10 ( 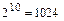) и т.д.

Для определения оптимальных значени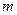й и 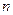воспользуемся критерием минимума произведения .

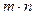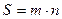
Как было отмечено ране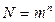е , где 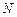- заданное число сообщений (число различных комбинаций сигнала). Логарифмируя, получим

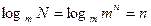
Следовательно,

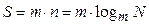
Используя формулу 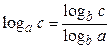, получим

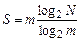
Условие минимума 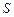примет вид:

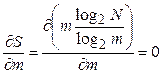
Воспользовавшись тождествами 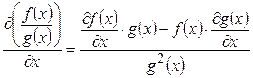, , 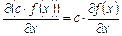, , 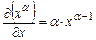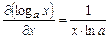получим

.

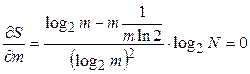Далее, используя тождество 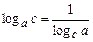, окончательно получим

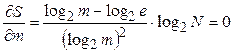
Из последнего тождества следует, что оптимальное значение 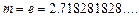Т.к. 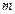должно быть целое, то оптимальным значением 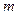является 3 или 2. На практике чаще используется основание кода .