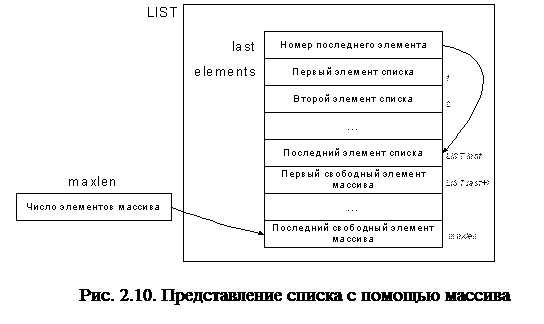
При реализации списков с помощью массивов элементы списка располагаются в смежных ячейках массива. На рис 2.10 представлена одна из возможных реализаций. В данном случае список представлен записью LIST, состоящей из поля last, указывающей на последний элемент списка и массива elements, в котором располагаются элементы списка. Поскольку элементы массива elements нумеруются с единицы, то значение last равно числу элементов списка. Длина массива elements храниться в константе maxlen.

Такое представление списка позволяет легко просматривать содержимое списка и вставлять новые элементы в его конец. Но вставка нового элемента в середину списка требует перемещения всех последующих элементов на одну позицию к концу массива, чтобы освободить место для нового элемента. Удаление элемента также требует перемещения элементов, чтобы закрыть освободившуюся ячейку.

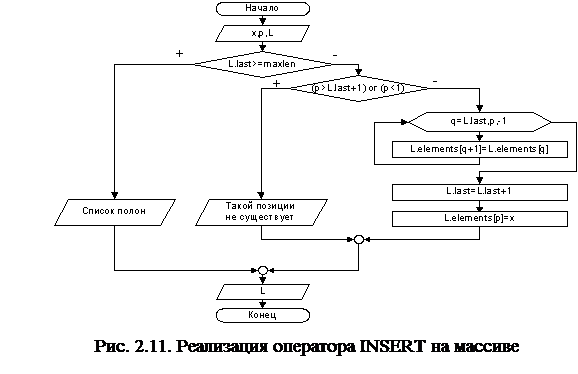
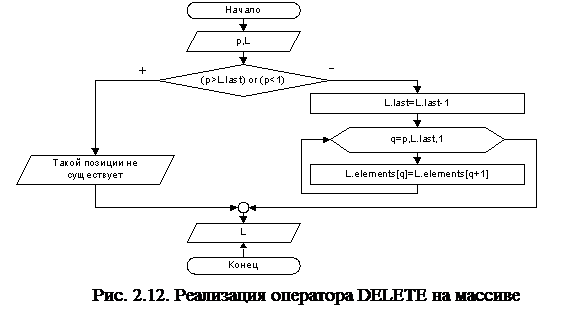
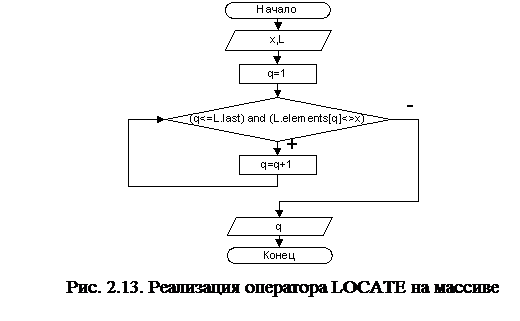
Алгоритмы операторов INSERT, DELETE и LOCATE списка, реализованного на массиве, представлены блок-схемами на рис. 2.11, 2.12 и 2.13 соответственно.

Реализацию остальных операторов списка сделайте самостоятельно.

Реализация списков с помощью указателей

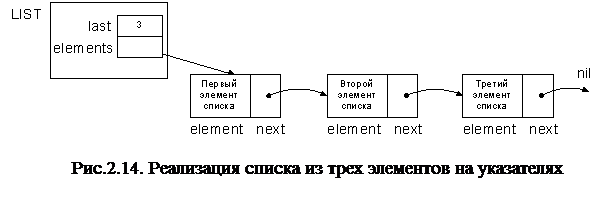
Реализация списков с помощью указателей освобождает от использования непрерывной области памяти для хранения списка. Это позволяет избавиться от перемещения элементов списка при вставке или удалении элементов. Однако ценой за это удобство становится дополнительная память для хранения указателей. Структура списка, реализованного с помощью указателей, представлена на рис.2.14. Список представлен записью LIST, состоящей из двух полей: last и elements. В поле last хранится число элементов списка, а в поле elements - указатель на первый элемент списка. Элемент списка хранится в записи, состоящей из двух полей: element и next. Поле element содержит значение элемента списка, а поле next - указатель на следующий элемент списка.

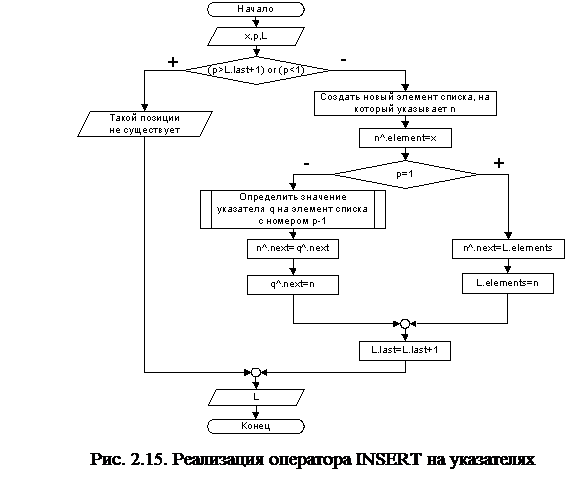
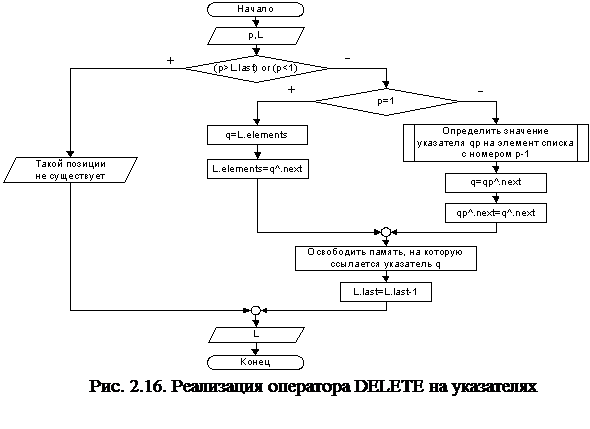
Реализация операторов INSERT и DELETE представлена блок-схемами на рис.2.15 и 2.16 соответственно.

Стеки

Стек - это специальный тип списка, в котором все вставки и удаления выполняются только на одном конце, называемом вершиной (top). Стеки иногда называют «магазинами», также для обозначения стеков используется аббревиатура LIFO (last-in-first-out - последний вошел - первый вышел). Интуитивными моделями стека могут служить патроны в магазине автоматического стрелкового оружия, книги, сложенные в стопку, или стопка тарелок; во всех этих моделях взять можно только верхний предмет, а добавить новый предмет можно, только положив его на верхний.

Абстрактные типы данных семейства STACK (cтек) обычно используют следующие пять операторов.

1. NULLSTACK(S). Делает стек S пустым. При реализации стека на списке S оператор NULLSTACK(S) эквивалентен NULLIST(S).

2. TOP(S). Возвращает элемент из вершины стека S. Если вершина стека соответствует первой позиции списка S, тогда TOP(S) можно записать в терминах общих операторов списка как RETRIVE(FIRST(S),S). Если вершина стека соответствует последней позиции списка S, тогда TOP(S) можно записать как RETRIVE(LAST(S),S).

3. POP(S). Удаляет элемент из вершины стека (выталкивает из стека). Если вершина стека соответствует первой позиции списка S, тогда этот оператор можно записать как DELETE(FIRST(S),S). Если вершина стека соответствует последней позиции списка S, тогда POP(S) записывается как DELETE(LAST(S),S). Иногда оператор POP(S) реализуется в виде функции, возвращающей удаляемый элемент.

4. PUSH(x,S). Вставляет элемент x в вершину стека S (заталкивает элемент в стек). Элемент, ранее находившийся в вершине стека, становится элементом, следующим за вершиной, и т.д. Если вершина стека соответствует первой позиции списка S, то данный оператор можно записать как INSERT(x,FIRST(S),S). Если вершина стека соответствует последней позиции списка S, то PUSH(x,S) записывается как INSERT(x, NEXT(LAST(S),S), S).

5. EMPTYSTACK(S). Эта функция возвращает значение true (истина), если стек S пустой, и значение false (ложь) в противном случае. При реализации стека на списке S оператор EMPTYSTACK(S) эквивалентен EMPTYLIST(S).

Очереди

Другой специальный тип списка - очередь (queue), где элементы вставляются с одного конца, называемого задним (rear), а удаляются с другого, переднего (front). Очереди также называют «списками типа FIFO» (аббревиатура FIFO расшифровывается как first-in-first-out: первым вошел - первым вышел). Операторы, выполняемые над очередями, аналогичны операторам стеков. Существенное отличие между ними состоит в том, что вставка новых элементов осуществляется в конец списка, а не в начало, как в стеках. Кроме того, различна устоявшаяся терминология для стеков и очередей.

1. NULLQUEUE(Q) очищает очередьQ, делая ее пустой. При реализации очереди на списке Q оператор NULLQUEUE(Q) эквивалентен NULLIST(Q).

2. FRONT(Q) - функция, возвращающая первый элемент очереди Q. Можно реализовать эту функцию с помощью операторов списка как RETRIEVE(FIRST(Q),Q).

3. ENQUEUE(x,Q) вставляет элемент x в конец очереди Q. С помощью операторов списка этот оператор можно выполнить следующим образом: INSERT(x, NEXT(LAST(Q),Q), Q).

4. DEQUEUE(Q) удаляет первый элемент очереди Q. C помощью операторов списка данный оператор записывается как DELETE(FIRST(Q),Q).

5. EMPTYQUEUE(Q) возвращает значение true тогда и только тогда, когда Q является пустой очередью. При реализации очереди на списке Q оператор EMPTYQUEUE(Q) эквивалентен EMPTYLIST(Q).

Графы и деревья

Понятия теории графов широко используются при формализации различных задач.

Пусть V - непустое множество, V^{2} - множество всех его двухэлементных подмножеств. Пара (V,E), где ЕÍV^{2}, называется неориентированным графом.

Элементы множества V называют вершинами графа, а элементы множества E – ребрами графа.

Ориентированным графом называется пара (V,E¢), где E¢ÍV´V= {(v₁,v₂)|v₁ÎV,v₂ÎV}. То есть в ориентированном графе важен порядок вершин, составляющих ребро. В ориентированных графах вместо термина «ребро» часто используют термин «дуга».

Если из контекста ясно, о каком графе идет речь, то ради сокращения речи вместо терминов «неориентированный граф» и «ориентированный граф» используют термин «граф».

Далее, если речь идет о графе G=(V,E), множество вершин будем обозначать VG, а множество ребер (дуг) - EG.

Граф G можно представить в виде некоторой геометрической структуры, состоящей из двух множеств: множества точек (вершин) VG и отрезков (ребер) ЕG, которые соединяют некоторые пары точек из VG. Если указаны начало и конец ребра, то отрезок заменяют направленным отрезком.

Две вершины u и v называются смежными вершинами, если множество {u,v} является ребром (дугой), и не смежными в противном случае. Также, в этом случае говорят, что u и v являются концевыми вершинами ребра e={u,v}. Для дуги e=(u,v) концевую вершину u называют началом, a v - концом дуги.

Смежными ребрами называются два ребра, имеющие общую концевую вершину.

Вершина v и ребро (дуга) е называются инцидентными, если v концевая вершина е, и не инцидентными в противном случае.

Ребро e={v,v} или дуга e=(v,v) называется петлей.

Ребра e₁={u,v},e₂={u,v},...,е_k={u,v} называются кратными ребрами.

Дуги e₁=(u,v),e₂=(u,v),...,е_k=(u,v) называются параллельными дугами.

Цепью называется любая последовательность попарно различных ребер (дуг), такая, что соседние ребра (дуги) в ней смежны. В орграфе если в цепи учтена ориентация дуг, то она называется путем.

Если не требовать, чтобы ребра (дуги) в упомянутой последовательности были различны, то получим понятие маршрута (ориентированного маршрута).

Циклом называется цепь, у которой начальная и конечная вершины совпадают.

Контуром называется путь, у которого начальная и конечная вершины совпадают.

Граф называется связным, если для каждой пары вершин найдется соединяющий их маршрут.

Граф, который не содержит циклов, называется ациклическим.

Связный неориентированный ациклический граф называется деревом, множество деревьев называется лесом.

Граф Н называется подграфом (или частью) графа G, если VHÍVG, ЕНÍEG. Если Н - подграф графа G, то говорят, что Н содержится в G.

Покрывающим (или остовным) деревом графа G называется дерево, являющееся подграфом графа G и содержащее все его вершины.

Если каждому ребру (дуге) графа поставлено в соответствие одно или несколько чисел, то такой граф называется взвешенным.