На Востоке, особенно в Китае, в процессе переговоров используется стратагемный подход,означающий применение неортодоксальных методов достижения целей. Везде, где требуется выигрыш в политической борьбе, необходимо стратагемное мышление. Этот подход подробно исследован И. А. Василенко, которая считает, что стратагемы подобны алгоритму, они организуют последовательность действий. На политических переговорах стратагемный подход раскрывается как сумма целенаправленных мероприятий, рассчитанных на реализацию долговременного стратегического плана, обеспечивающего решение кардинальных задач.

Наиболее эффективно на политических переговорах могут быть использованы следующие стратагемы: “Объединиться с дальним врагом, чтобы победить ближнего”, “Превратить роль гостя в роль хозяина”, Заманить на крышу и убрать лестницу”, “Ловить рыбу в мутной воде”, “На востоке поднимать шум, на западе нападать”, “Скрывать за улыбкой кинжал”, “Осадить Вэй, чтобы спасти Чжао”, “Сманить тигра с горы на равнину”, “Тайно подкладывать хворост под костер другого”, “Убить чужим ножом”, “Обмануть императора, чтобы он переплыл море” и др.

Еще в древнем Китае была детально разработана методика применения той или иной стратагемы с учетом различных обстоятельств и ситуаций. Основная идея стратагемного мышления на переговорах - не вступать в прямое противоборство, открыто не конфликтовать, что способно завести переговоры в тупик, быстро истощить силы и нанести невосполнимый урон партнерским отношениям. С помощью тайных уловок “задушить в объятьях” партнеров по переговорам и сохранить свои силы и богатства: “ Каждый человек стоит на линии фронта. Краткий миг рассеянности - и вот уже что-то, принадлежащее одному человеку, досталось в добычу другому. Но тот, кто умеет применять стратагемы, всегда удержит инициативу в своих руках”.

Диаграмма Ганта

Диаграмма Ганта (также называемая «ленточной»), которая представляет собой диаграмму интервалов на шкале времени. Наиболее типичное использование диаграммы Ганта – визуальное отражение хода выполнения какого-либо проекта.

Диагра́мма Га́нта (англ. Gantt chart, также ленточная диаграмма, график Ганта) — это популярный тип столбчатых диаграмм, который используется для иллюстрации плана, графика работ по какому-либо проекту. Является одним из методов планирования проектов.

Первый формат диаграммы был разработан Генри Л. Гантом (Henry L. Gantt, 1861‒1919) в 1910 году.

Диаграмма Ганта представляет собой отрезки (графические плашки), размещенные на горизонтальной шкале времени. Каждый отрезок соответствует отдельной задаче или подзадаче. Задачи и подзадачи, составляющие план, размещаются по вертикали. Начало, конец и длина отрезка на шкале времени соответствуют началу, концу и длительности задачи. На некоторых диаграммах Ганта также показывается зависимость между задачами. Диаграмма может использоваться для представления текущего состояния выполнения работ: часть прямоугольника, отвечающего задаче, заштриховывается, отмечая процент выполнения задачи; показывается вертикальная линия, отвечающая моменту «сегодня».

Часто диаграмма Ганта соседствует с таблицей со списком работ, строки которой соответствуют отдельно взятой задаче, отображенной на диаграмме, а столбцы содержат дополнительную информацию о задаче. Пример такой таблицы представлен ниже.

Диаграмма Ганта может использоваться для наглядного представления таких данных как:

• ход выполнения проекта;
• график рабочего времени;
• графиков отпусков;
• использование оборудования;
• занятость помещений;
• и другие.

В типичной диаграмме Ганта отдельные задачи и операции проекта перечислены с левой стороны диаграммы, шкала времени отображается сверху, а длительности каждой задачи и операции показаны горизонтальными полосками (лентами) от даты начала до даты завершения

Гибкое представление данных

Диаграмма Ганта имеет гибкую структуру данных. Как точки, так и серии представляют собой иерархические коллекции, что позволяет, например, представить проект как набор связанных, иерархических задач.

Множество серий позволяет на одной диаграмме отображать разные данные, например: отпуска, командировки и отсутствие по болезни.

Каждая серия, точка, значение (совокупность интервалов) и интервал имеет расшифровку, что позволяет производить детализацию выбранного значения.

PERT

Program Evaluation and Review Technique (сокращенно PERT) — техника оценки и анализа программ, которая используется при управлении проектами. Была разработана в 1958 году консалтинговой фирмой «Буз, Ален и Гамильтон» совместно с корпорацией «Локхид» по заказу Подразделения специальных проектов ВМС США в составе Министерства Обороны США для проекта создания ракетной системы «Поларис» (Polaris). Проект «Поларис» был ответом на кризис, наступивший после запуска Советским Союзом первого космического спутника.

PERT — это способ анализа задач, необходимых для выполнения проекта. В особенности, анализа времени, которое требуется для выполнения каждой отдельной задачи, а также определение минимального необходимого времени для выполнения всего проекта.

PERT был разработан в 50-ые годы главным образом для упрощения планирования и составления графиков больших и сложных проектов. Метод подразумевал наличие неопределённости, давая возможность разработать рабочий график проекта без точного знания деталей и необходимого времени для всех его составляющих.

Самая известная часть PERT — это «Сети PERT» — графики соединённых между собой временных линий. PERT предназначен для очень масштабных, единовременных, сложных, нерутинных проектов.

Диаграмма представляет собой множество точек-вершин вместе с соединяющими их ориентированными дугами. Каждая из них как направленный отрезок имеет начало и конец, причем модель содержит только одну из пары симметричных дуг (от вершины 1 к вершине 2 и от вершины 2 к вершине 1). Всякой дуге, рассматриваемой в качестве какой-то работы из числа нужных для осуществления проекта, приписываются определенные количественные характеристики. Это — объемы выделяемых на нее ресурсов и, соответственно, ее ожидаемая продолжительность (длина дуги). Любая вершина интерпретируется как событие завершения работ, представленных дугами, которые входят в нее, и одновременно начала работ, отображаемых дугами, исходящими оттуда. Таким образом, фиксируется что ни к одной из работ нельзя приступить прежде чем будут выполнены все предшествующие ей согласно технологии реализации проекта. Факт начала этого процесса — вершина без входящих, а окончание — без исходящих дуг. Остальные вершины должны иметь и те, и другие. Последовательность дуг, в которой конец каждой предшествующей совпадает с началом последующей, трактуется как путь от отправной вершины к завершающей, а сумма длин таких дуг — как его продолжительность. Обычно начало и конец реализации проекта связаны множеством путей, длины которых различаются. Наибольшая определяет длительность всего этого проекта, минимально возможную при зафиксированных характеристиках дуг графа. Соответствующий путь — критический и в каждый момент времени контролировать нужно состояние именно тех работ, которые «лежат» на нем.

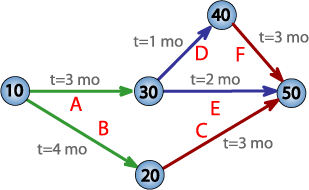
Пример сетевой PERT диаграммы для проекта продолжительностью в семь месяцев с пятью промежуточными точками (от 10 до 50) и шестью деятельностями (от A до F).

Сетевые графики

Сетевой график основан на использовании другой математической модели - графа. Графам (устаревшие синонимы: сеть, лабиринт, карта и т.д.) математики называют "множество вершин и набор упорядоченных или неупорядоченных пар вершин". Говоря более привычным для инженера (но менее точным) языком, граф - это набор кружков (прямоугольников, треугольников и проч.), соединенных направленными или ненаправленными отрезками. В этом случае сами кружки (или другие используемые фигуры) по терминологии теории графов будут называться "вершинами", а соединяющие их ненаправленные отрезки - "ребрами", направленные (стрелки) - "дугами". Если все отрезки являются направленными, граф называется ориентированным, если ненаправленными - неориентированным. Основными понятиями являются — работа, события, пути. Виды работ Действительная работа в прямом смысле слова (например — подготовка трассы соревнований), требующая затрат труда, материальных ресурсов и времени; Ожидание — работа не требующая затрат труда и материальных ресурсов, но занимающая некоторое время; Фиктивная работа (Зависимость) — связь между двумя или более событиями, не требующая затрат труда, материальных ресурсов и времени, но указывающая, что возможность начала одной операции непосредственно зависит от выполнения другой. Продолжительность такой работы = 0. Всякая работа в сети соединяет два события: предшествующее (являющееся для нее начальным) и следующее за ней (конечное). Виды событий Исходное событие — начало выполнения комплекса работ; Завершающее событие — конечное событие, означающее достижение конечной цели комплекса работ; Промежуточное событие, как результат одной или нескольких работ, представляющих возможность начать одну или несколько непосредственно следующих работ. Продолжительность промежуточного события во времени всегда = 0. Событие определяет состояние, а не процесс. Пути Любая последовательность работ в сетевом графике, в котором конечное событие каждой работы этой последовательности совпадает с начальным событием следующей за ней работой, называется путем. Пути в сетевом графике могут быть трех видов: Полный путь — начало которого совпадает с исходным событием сети, а конец — с завершающим, называется полным путем; Путь, предшествующий событию — путь от исходного события сети до данного события; Путь, следующий за событием — путь, соединяющий событие с завершающим событием; Путь между событиями i и j — путь, соединяющий какие-либо два события i и j, из которых ни одно не является исходным или завершающим событием сетевого графика; Критический путь — путь, имеющий наибольшую продолжительность от исходного события до завершающего. Правила составления сетевых графиков Каждая работа должна быть заключена между двумя событиями. В сети не может быть работ, имеющих одинаковые коды. В сети не должно быть событий, на которых не выходит ни одной работы, если только это событие не является для данного графика завершающим. Соответственно, в сети не должно быть события, в которое не входит ни одной работы, если только это событие не является исходным. В сетевом графике не должно быть замкнутых контуров. Сетевой график — это динамическая модель производственного процесса, отражающая технологическую зависимость и последовательность выполнения комплекса работ, увязывающая их свершение во времени с учетом затрат ре­сурсов и стоимости работ с выделением при этом узких (критических) мест. Основные элементы сетевого графика — работа и событие. Работа отражает трудовой процесс, в котором участвуют люди, машины, механизмы, материальные ресурсы (проектирование сооружения, поставки оборудования, кладка стен, решение задач на ЭВМ и т. п.) либо процесс ожидания (твердение бетона, сушка штукатурки и т. п.). Каждая работа сетевого графика имеет конкретное содержание. Работа как трудовой процесс требует затрат времени и ресурсов, а как ожидание — только времени. Для правильного и наглядного отображения порядка предшествования работ при построении сети используют изображаемые штриховыми линиями дополнительные дуги, называемые фиктивными рабо­тами или связями. Они не требуют ни времени, ни ресурсов, а лишь указывают, что начало одной работы зависит от окончания другой. Событие выражает факт окончания одной или нескольких непосредственно предшествующих (входящих в событие) работ, необходимых для начала непосредственно следующих (выходящих из события) работ. Событие, стоящее в начале работы, называется начальным, а в конце-конечным. Начальное событие сетевого графика называется исходным, а конечное — завершающим. Событие, не являющееся ни исходным, ни завершающим, называется промежуточным. В исходное событие сетевого графика не входит, а из завершающего не выходит ни одна работа. В отличие от работ, события совершаются мгновенно без потребления ресурсов. Обозначение непосредственно предшествующих и непосредственно следующих работ. Любая последовательность работ в сетевом графике, при котором конечное событие каждой работы совпадает с начальным событием последующей, называется путем. Продолжительность пути определяется суммой продолжительностей составляющих его работ. Путь наибольшей длины между исходными и завершающими событиями называется критическим (Lm). Если критическое время не соответствует заданному или нормативному, сокращение сроков производственного процесса необходимо начинать с сокращения продолжительности критических работ. Наиболее распространенный тип сетевого графика работ представляет систему кружков и соединяющих их направленных отрезков (стрелок), где стрелки отображают сами работы, а кружки на их концах ("события") - начало или окончание этих работ. Рисунок показывает упрощенно лишь одну из возможных конфигураций сетевого графика, без данных, характеризующих сами планируемые работы. Фактически на сетевом графике приводится множество сведений о производимых работах. Над каждой стрелкой пишется наименование работы, под стрелкой - продолжительность, этой работы (обычно в днях). В самих кружках (разделенных на секторы) также содержится информация, смысл которой будет пояснен в дальнейшем. Фрагмент возможного сетевого графика с такими данными представлен на рисунке ниже. В графике могут использоваться пунктирные стрелки - это так называемые "зависимости" (фиктивные работы), не требующие ни времени, ни ресурсов. Они указывают на то, что "событие", на которое направлена пунктирная стрелка, может происходить только после свершения события, из которого исходит эта стрелка. В сетевом графике не должно быть тупиковых участков, каждое событие должно соединяться сплошной или пунктирной стрелкой (или стрелками) с каким-либо предшествующим (одним или несколькими) я последующим (одним или несколькими) событиями. Нумерация событий производится примерно в той последовательности, в какой они будут происходить. Начальное событие располагается обычно с левой стороны графика, конечное — с правой. Последовательность стрелок, в которой начало каждой последующей стрелки совпадает с концом предыдущей, называется путем. Путь обозначается в виде последовательности номеров событий. В сетевом графике между начальным и конечным событиями может быть несколько путей. Путь, имеющий наибольшую продолжительность, называется критическим. Критический путь определяет общую продолжительность работ. Все остальные пути имеют меньшую продолжительность, и поэтому в них выполняемое работы имеют резервы времени. Критический путь обозначается на сетевом графике утолщенными или двойными линиями (стрелками). Особое значение при составлении сетевого графика имеют два понятия: Раннее начало работы - срок, раньше которого нельзя начать данную работу, не нарушив принятой технологической последовательности. Он определяется наиболее долгим путем от исходного события до начала данной работы Позднее окончание работы - самый поздний срок окончания работы, при котором не увеличивается общая продолжительность работ. Он определяется самым коротким путем от данного события до завершения всех работ. При оценке резервов времени удобно использовать еще два вспомогательных понятия: Раннее окончание - срок, раньше которого нельзя закончить данную работу. Он равен раннему началу плюс продолжительность данной работы Позднее начало - срок, позже которого нельзя начинать данную работу, не увеличив общую продолжительность строительства. Он равен позднему окончанию минус продолжительность данной работы. Если событие является окончанием лишь одной работы (т.е. в него направлена только одна стрелка), то раннее окончание этой работы совпадает с ранним началом последующей. Общий (полный) резерв - это наибольшее время, на которое можно задержать выполнение данной работы, не увеличивая общую продолжительность работ. Он определяется разностью между поздним и ранним началом (или поздним и ранним окончанием - что то же самое). Частный (свободный) резерв - это наибольшее время, на которое можно задержать выполнение данной работы, не меняя раннего начала последующей. Этот резерв возможен только тогда, когда в событие входят две или более работы (зависимости), т.е. на него направлены две или более стрелки (сплошные или пунктирные). Тогда лишь у одной из этих работ раннее окончание будет совпадать с ранним началом последующей работы, для остальных же это будут разные значения. Эта разница у каждой работы и будет ее частным резервом. Кроме описанного типа сетевых графиков, в котором вершины графа ("кружки") отображают события, а стрелки - работы, существует другой тип, в котором вершинами являются работы. Различие между этими типами непринципиальное - все основные понятия (раннее начало, позднее окончание, общие и частные резервы, критический путь и т.д.) сохраняются неизменными, отличаются лишь способы их записи. Построение сетевого графика этого типа основано на том, что раннее начало последующей работы равно раннему окончанию предыдущей. Если данной работе предшествует несколько работ, ее раннее качало должно быть равно максимальному раннему окончанию предыдущих работ. Расчет поздних сроков ведется в обратном порядке - от завершающий к исходной, как и В сетевом графике "вершины - события". У завершающей работы позднее и раннее окончание совпадают и отражают продолжительность критического пути. Позднее начало последующей работы равно позднему окончанию предыдущей. Если за данной работой следует несколько работ, то определяющим является минимальное значение из поздних начал. Сетевые графики "вершины - работы" появились позже графиков "вершины - события", поэтому они несколько менее известны и сравнительно реже описываются в учебной и справочной литературе. Тем не менее, они имеют свои преимущества, в частности их легче строить и легче корректировать. При корректировка графиков ''вершены — работы" их конфигурация не меняется, у графиков же "вершины - события" такие изменения исключить не удается. Однако в настоящее время составление и корректировка сетевых графиков автоматизированы, и для пользователя, которому важно знать лишь последовательность работ и их резервы времени, не имеет особого значения, каким способом сделан график, т.е. какого он типа. В современных специализированных пакетах компьютерных программ планирования и оперативного управления в основном используется тип "вершины - работы". Корректировка сетевых графиков производится как на этапе их составления, так и использования. Она состоит в оптимизации строительных работ по времени и по ресурсам (в частности по движению рабочей силы). Если, например, сетевой график не обеспечивает выполнения работ в необходимые сроки (нормативные или установленные контрактом) производится его корректировка по времени, т.е. сокращается продолжительность критического пути. Обычно это делается за счет резервов времени некритических работ и соответствующего перераспределения ресурсов за счет привлечения дополнительных ресурсов за счет изменения организационно-технологической последовательности и взаимосвязи работ. В последнем случае у графиков "вершины - события" приходится менять их конфигурацию (топологию). Корректировка по ресурсам производится путем построения линейных календарных графиков по ранним началам, соответствующих тому или иному варианту сетевого графика, и корректировки этого варианта. Автоматизированные системы управления строительством обычно включают компьютерные программы, в той или иной мере автоматизирующие практически все этапы составления и корректировки сетевых графиков.

Метод критического пути

Метод критического пути — эффективный инструмент планирования расписания и управления сроками проекта.

В основе метода лежит определение наиболее длительной последовательности задач от начала проекта до его окончания с учетом их взаимосвязи. Задачи лежащие на критическом пути (критические задачи) имеют нулевой резерв времени выполнения и в случае изменения их длительности изменяются сроки всего проекта. В связи с этим при выполнении проекта критические задачи требуют более тщательного контроля, в частности, своевременного выявления проблем и рисков, влияющих на сроки их выполнения и, следовательно, на сроки выполнения проекта в целом. В процессе выполнения проекта критический путь проекта может меняться, так как при изменении длительности задач некоторые из них могут оказаться на критическом пути.

Расчёт критического пути

Если начальный момент выполнения проекта положить равным нулю, то сроки окончания у первых работ сетевого графика, то есть работ, выходящих из первого события, будет определяться их продолжительностью. Время наступления любого события следует положить равным самому позднему времени окончания непосредственно входящих в это событие работ: считается, что работа в сетевом графике не может начаться, пока не завершены все предшествующие для нее работы.

В процессе решения — методом «эстафеты» — просматриваются все дуги сетевого графика. Пусть очередная просматриваемая дуга связывает вершины i и j. Если для вершины i определено предположительное время его свершения и это время плюс продолжительность работы больше предположительного времени наступления события j, тогда для вершины j устанавливается новое предположительное время наступления, равное предположительному времени наступления события i плюс продолжительность работы рассматриваемой дуги. Решение заканчивается, когда очередной просмотр дуг не вызывает ни одного исправления предположительного значения времени начала/окончания работ/событий. В результате может быть определено событие с самым поздним временем наступления, и путь от начальной вершины в эту конечную будет считаться критическим и определять продолжительность выполнения проекта. Наряду с общей продолжительностью выполнения проекта, критический путь определяет другие характеристики сетевого графика, играющие важную роль при планировании реализации нововведения, минимизации сроков и расходов на разработку.

Суть решения задачи сокращения сетевого графика сводится к привлечению дополнительных ресурсов к выполнению работ, лежащих на критическом пути, снятием работ, не лежащих на критическом пути, запараллеливанием работ.

метод критической цепи: