Заметив, что функция 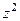 аналитическая, т.е. для неё выполняются условия Коши-Римана, можно не раскрывать скобки предыдущим способом, а вычислить первообразную по
аналитическая, т.е. для неё выполняются условия Коши-Римана, можно не раскрывать скобки предыдущим способом, а вычислить первообразную по 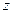 в начальной и конечной точке.
в начальной и конечной точке.
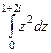 =
= 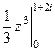 =
= 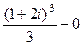 , а дальше всё сводится просто к вычислению степени комплексного числа.
, а дальше всё сводится просто к вычислению степени комплексного числа.
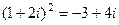
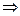
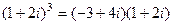 =
=  , тогда
, тогда
 =
= 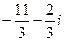 .
.
Ответ. 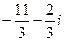
Задача 58. Вычислить 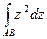 по участку единичной окружности в 1-й четверти от 1 до
по участку единичной окружности в 1-й четверти от 1 до 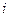 .
.
Решение. Здесь тоже можно вычислять как без, так и по формуле Ньютона-Лейбница. Но разница в объёме вычислений будет огромная.
Так как функция аналитическая, нам не важно, соединены точки по дуге окружности или по какой-то другой линии, на самом деле результат зависит только от первообразной в начальной и конечной точках. Сделаем по формуле Ньютона-Лейбница.
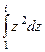 =
= 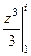 =
=  =
=  =
= 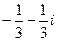 .
.
Ответ. 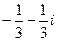 .
.
Задача 59. Вычислить 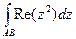 по отрезку от 0 до
по отрезку от 0 до 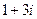 .
.
Решение. Так как  , то функция не аналитическая, т.к. частные производные от
, то функция не аналитическая, т.к. частные производные от 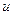 будут какие-то функции, а от
будут какие-то функции, а от 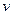 нулевые, и точно не не будет совпадений, которые нужны для условий Коши-Римана. Поэтому формулу Ньютона-Лейбница здесь применить нельзя, а только универсальный способ с разложением на
нулевые, и точно не не будет совпадений, которые нужны для условий Коши-Римана. Поэтому формулу Ньютона-Лейбница здесь применить нельзя, а только универсальный способ с разложением на 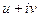 . Отрезок от (0,0) до (1,3), он характеризуется явным уравнением
. Отрезок от (0,0) до (1,3), он характеризуется явным уравнением 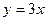 , при этом
, при этом  ,
, 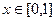 .
.
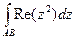 =
= 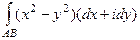 =
= 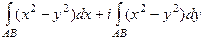 =
=
 =
= 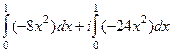 =
=
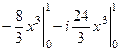 =
=  .
.
Ответ. 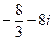 .
.
Задача 60. Вычислить  .
.
Решение. Несмотря на то, что здесь интеграл по замкнутому контуру, применять интегральную формулу Коши нельзя, ведь функция не аналитическая, т.е. аналитичность нарушена не в изолированных точках, а во всей плоскости.
Сделаем разложение функции на Re и Im.
 =
= 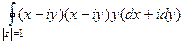 =
= 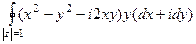 =
= 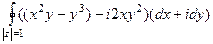 =
=
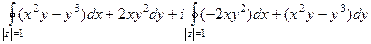 .
.
После этого введём обычную для такой единичной окружности параметризацию через 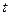 :
: 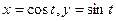 , где
, где 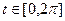 .
.
При этом 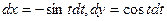 . После того, как выразим через
. После того, как выразим через 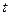 , получается такое выражение, записанное в две строки:
, получается такое выражение, записанное в две строки:
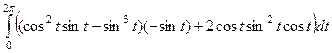 +
+
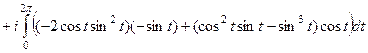 .
.
Если привести подобные, то:

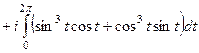 =
=
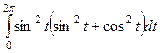
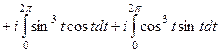
далее в действительной части используем формулу понижения степени, а в мнимой части подведение под знак дифференциала.
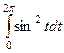
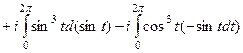 =
=
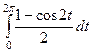
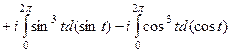 =
=

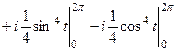
в мнимой части все интегралы окажутся 0, так как на верхнем и нижнем пределе 0 и 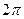 , а тригонометрические функции совпадают в точках, отличающихся на
, а тригонометрические функции совпадают в точках, отличающихся на 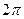 , значит, формула Ньютона-Лейбница приведёт к 0.
, значит, формула Ньютона-Лейбница приведёт к 0.
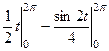
 =
=
 =
= 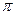 .
.
Ответ.  .
.
Задача 61. Вычислить 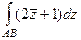 , где АВ - участок кубической параболы
, где АВ - участок кубической параболы 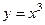 от (0,0) до (1,1).
от (0,0) до (1,1).
Решение. 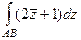 =
= 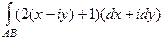 =
=
 =
= 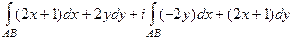 .
.
Теперь сведём все получившиеся криволинейные интегралы к одной лишь переменной 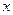 , заменяя
, заменяя 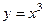 и
и 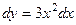 , где
, где 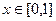 .
.
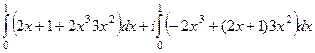 =
=
= 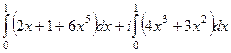 =
=
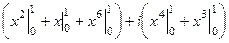 =
= 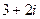 .
.
Ответ.  .
.
Задача 62. Вычислить 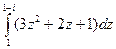 .
.
Решение. Здесь сумма степенных функций, они являются аналитическими. Поэтому используем формулу Ньютона-Лейбница.
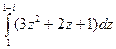 =
=  =
=  .
.
Отдельно вычислим 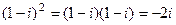 ,
,
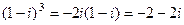 .
.
Тогда 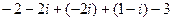 =
=  .
.
Ответ.  .
.
Задача 63. Вычислить 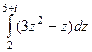 .
.
Решение. 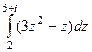 =
= 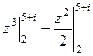 =
= 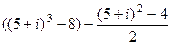 .
.
Вычислим квадрат и куб этого числа. 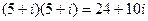 ,
,
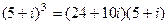 =
= 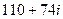 .
.
Тогда 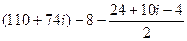 =
= 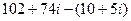 =
=
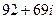 .
.
Ответ. 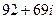 .
.
Задача 64. Вычислить 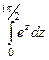 .
.
Решение. Можно применять формулу Ньютона-Лейбница, так как функция  аналитическая.
аналитическая.
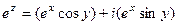 , тогда:
, тогда:
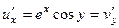 ,
, 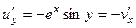 .
.
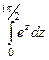 =
=  =
= 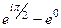 =
=  =
=  =
=
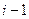 =
= 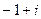 .
.
Ответ. 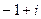 .
.
Интегральная формула Коши.
Следующая серия задач решается с помощью формул Коши:
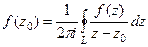 и
и 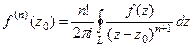 .
.
Здесь будут комбинированные задачи, состоящие из нескольких подзадач, где контур проводится сначала вокруг той или иной точки разрыва, а затем вокруг всех этих точек.
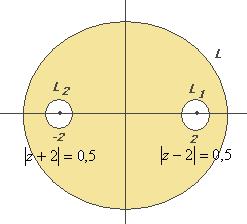
Задача 65. Вычислить 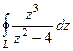 , где контур
, где контур 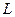 :
:
А) 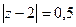 Б)
Б) 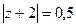 В)
В) 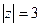 .
.
Решение. В знаменателе разложим на множители, и станет видно, что корни многочлена там 2 и 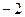 .
.
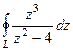 =
= 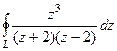 .
.
Если контур радиуса 0,5 окружает одну из точек, то надо применить интегральную формулу Коши, где точка 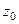 одна из них, а именно, в первом пункте
одна из них, а именно, в первом пункте 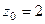 , а во втором
, а во втором 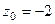 . Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное
. Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное 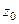 вместо
вместо 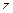 в оставшейся части функции.
в оставшейся части функции.
А) 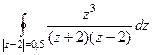 =
=  =
= 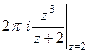 =
=  =
= 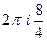 =
=  .
.
Б)  =
= 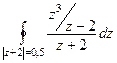 =
= 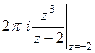 =
= 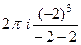 =
= 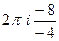 =
=  .
.
В) В третьем пункте, где контур окружает уже обе точки, достаточно будет воспользоваться теоремой Коши и суммировать результаты двух предыдущих пунктов. Получится 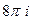 .
.
Ответы. А) 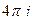 Б)
Б) 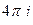 В)
В) 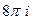 .
.
Задача 66. Вычислить 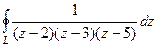 , где контур
, где контур 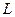 :
:
А) 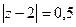 Б)
Б) 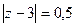 В)
В) 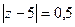 Г)
Г) 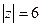 Д)
Д) 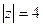 .
.
Решение. В каждом случае применяем интегральную формулу Коши к той или иной точке разрыва функции, 2, 3 и 5. Убирая соответствующий множитель из знаменателя, затем подставляем в оставшуюся часть функции это число.
А) 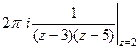 =
= 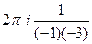 =
= 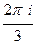 .
.
Б)  =
= 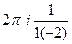 =
= 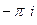 .
.
В)  =
= 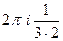 =
= 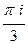 .
.
Если радиус 6, то все 3 точки находятся внутри контура. Суммируем все 3 результата:
Г) 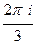
 +
+  = 0 .
= 0 .
В последнем случае, лишь две из трёх точек внутри контура:
Д) 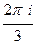
 =
= 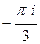 .
.
Ответы. А) 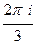 Б)
Б) 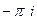 В)
В)  Г) 0 Д)
Г) 0 Д) 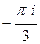 .
.
Задача 67. Вычислить 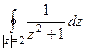 .
.
Решение. 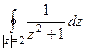 =
= 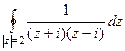 . Здесь две особые точки, это
. Здесь две особые точки, это  , они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.
, они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.
 =
= 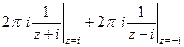 =
=
 =
= 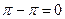 .
.
Ответ. 0.
Задача 68. Вычислить 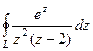 , где контур
, где контур 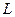 :
:
А) 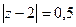 Б)
Б)  В)
В) 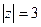 .
.
Решение. В 1 пункте здесь корень 2 соответствует 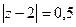 , а во втором корень 0, но он имеет кратность 2, поэтому надо будет сделать по обобщённой интегральной формуле Коши, то есть с помощью производной.
, а во втором корень 0, но он имеет кратность 2, поэтому надо будет сделать по обобщённой интегральной формуле Коши, то есть с помощью производной.
А) 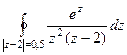 =
= 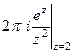 =
= 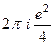 =
=  .
.
Б) Здесь корень 0, он соответствует множителю 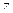 , который, впрочем, можно было бы записать в виде скобки
, который, впрочем, можно было бы записать в виде скобки 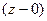 .
.
Конкретизируем обобщённую формулу Коши для 2 степени:
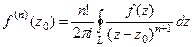 , при n=1:
, при n=1: 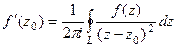
Тогда 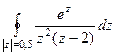 =
= 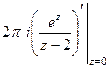 =
= 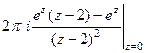 =
=
 =
= 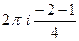 =
= 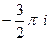 .
.
В) Здесь внутри контура обе особые точки, рассмотренные в предыдущих пунктах. По интегральной теореме Коши просто складываем результаты, полученные в 2 предыдущих пунктах. Получаем 
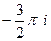 .
.
Ответы. А)  Б)
Б) 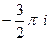 В)
В) 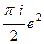
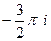 .
.
Задача 69. Вычислить 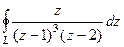 , где контур
, где контур 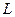 :
:
А) 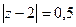 Б)
Б) 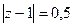 В)
В) 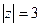 .
.
Решение.
А) 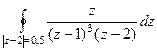 =
= 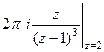 =
=  =
=  .
.
Б) В этом случае корень знаменателя имеет кратность 3, так что придётся считать с помощью 2-й производной.
Конкретизируем обобщённую формулу Коши для 3 степени:
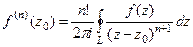 , при n=2:
, при n=2: 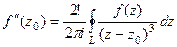 . Тогда
. Тогда 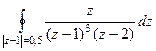 =
= 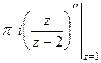 =
=
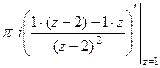 =
= 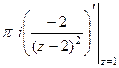 =
= 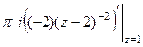 =
= 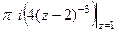 =
=  =
= 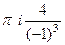 =
=  .
.
В) 
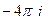 = 0 .
= 0 .
Ответы. А) 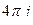 Б)
Б) 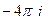 В) 0 .
В) 0 .
Задача 70. Вычислить 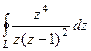 , где контур
, где контур 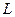 :
:
А) 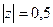 Б)
Б) 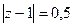 В)
В) 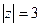 .
.
Решение.
А) 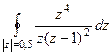 =
= 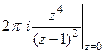 =
=  = 0.
= 0.
Б) 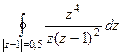 =
= 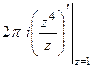 =
= 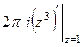 =
= 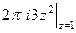 =
= 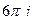 .
.
В) 0+ 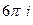 =
= 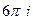 .
.
Ответы. А) 0 Б) 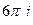 В)
В) 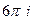 .
.
Задача 71. Вычислить 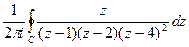 , где контур
, где контур 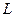 :
:
А) 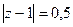 Б)
Б) 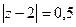 В)
В) 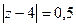 Г)
Г) 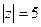 .
.
Решение. Так как здесь в интеграле уже изначально есть множитель 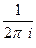 , то домножать на
, то домножать на 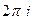 в правой части не нужно.
в правой части не нужно.
А)  =
= 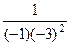 =
= 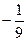 .
.
Б) 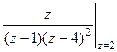 =
=  =
= 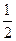 .
.
В) В отличие от двух первых точек, здесь в знаменателе корень 2-го порядка, поэтому подставляем 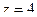 не сразу, а после вычисления производной.
не сразу, а после вычисления производной.
 =
=  =
= 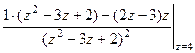 =
= 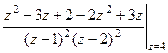 =
= 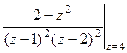 =
= 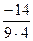 =
= 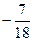 .
.
Г) По интегральной теореме Коши, сумма интегралов по трём предыдущим контурам: 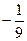 +
+ 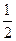
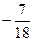 = 0 .
= 0 .
Ответы. А) 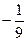 Б)
Б) 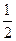 В)
В) 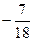 Г) 0.
Г) 0.
Задача 72. Вычислить 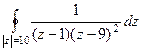 .
.
Решение. Здесь две особые точки, 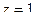 полюс 1-го порядка и
полюс 1-го порядка и  полюс 2-го порядка. Для 2-й точки надо применять обобщённую формулу Коши (с производной).
полюс 2-го порядка. Для 2-й точки надо применять обобщённую формулу Коши (с производной).
 =
=  =
=
 =
= 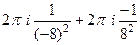 =
=
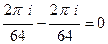 .
.
Ответ. 0.
Задача 73. Вычислить 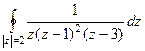 .
.
Решение. Внутри окружности радиуса 2 лежат 2 из 3 особых точек, а именно, 0 и 1, точка 3 снаружи.
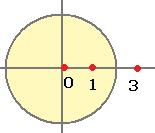
Поэтому интегральную формулу Коши применяем только к двум точкам.
 =
=  .
.
Предварительно вычислим производную.
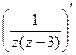 =
= 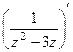 =
= 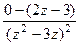 =
= 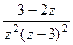 .
.
Далее, 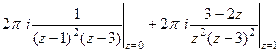 =
=
 =
= 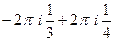 =
=
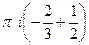 =
= 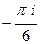 .
.
Ответ.  .
.
Задача 74. Вычислить  .
.
Решение. Здесь степень множителя в знаменателе равна 2. Есть всего одна точка разрыва, а именно 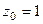 . Конкретизируем обобщённую интегральную формулу Коши для этого случая.
. Конкретизируем обобщённую интегральную формулу Коши для этого случая.
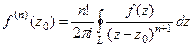 , при n = 1 получается
, при n = 1 получается
 =
= 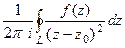 .
.
Отсюда следует, что 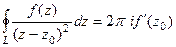
Тогда  =
= 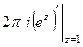 =
=  =
= 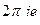 .
.
Ответ. 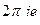 .
.
Задача 74-Б. Вычислить 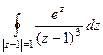 .
.
Решение. Здесь степень множителя в знаменателе равна 3. Есть всего одна точка разрыва, а именно 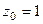 .
.
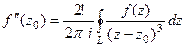 =
= 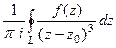 .
.
Отсюда следует, что 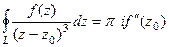
Тогда 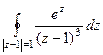 =
= 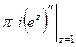 =
= 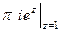 =
= 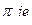 .
.
Ответ. 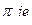 .
.
Задача 75. Вычислить 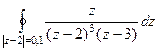 .
.
Решение. 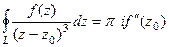 , тогда
, тогда 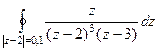 =
= 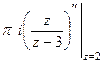 =
= 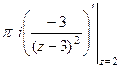 =
=  =
= 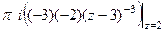 =
= 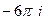
Ответ. 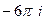 .
.
Особые точки и вычеты.
Задача 76. Найти все особые точки и определить их тип для функции 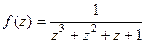 .
.
Решение. Здесь нужно сначала преобразовать выражение в знаменателе, выделить множители, соответствующие каждому корню.
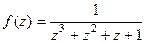 =
= 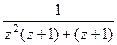 =
= 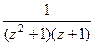 =
=  . Таким образом, полюсы 1-го порядка:
. Таким образом, полюсы 1-го порядка: 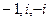 .
.
Ответ. Полюсы 1-го порядка: 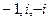 .
.
Задача 77. Найти все особые точки и определить их тип для функции  .
.
Решение. Разложим знаменатель на множители, предварительно найдём корни с помощью дискриминанта.
 =
=  =
= 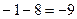 .
. 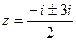 , корни
, корни 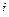 ,
,  .
.
Тогда 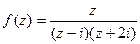 . Для знаменателя
. Для знаменателя 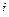 и
и 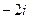 нули порядка 1, значит, для функции это полюсы порядка 1.
нули порядка 1, значит, для функции это полюсы порядка 1.
Ответ. Полюсы 1-го порядка: 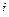 ,
,  .
.
Задача 78. Найти все особые точки и определить их тип для функции 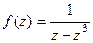 .
.
Решение. Разложим знаменатель на множители,
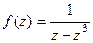 =
=  =
= 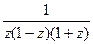 .
.
При  ,
,  ,
,  нули 1-го порядка в знаменателе, тогда для функции это полюсы 1 порядка.
нули 1-го порядка в знаменателе, тогда для функции это полюсы 1 порядка.
Ответ. Полюсы 1-го порядка: 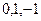 .
.
Задача 79. Исследовать тип особой точки 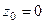 для
для  .
.
Решение. Здесь в знаменателе 3-я степень, но в этой точке в числителе тоже 0, и он влияет на итоговый порядок полюса. Надо в числителе разложить в ряд, чтобы остались одни лишь только степенные функции, потом вынесем за скобку минимальную степень, и это будет определять порядок нуля в числителе.
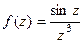 =
= 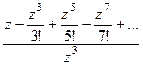 =
= 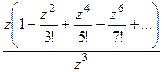
В числителе и знаменателе нули соответственно 1-го и 3-го порядка. После сокращения на 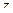 видно, что полюс 2 порядка, так как в скобках осталась функция, не стремящаяся к 0 в
видно, что полюс 2 порядка, так как в скобках осталась функция, не стремящаяся к 0 в 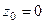 .
.
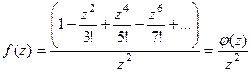 .
.
Ответ. 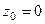 полюс 2 порядка.
полюс 2 порядка.
Дата: 2019-11-01, просмотров: 291.