Необходимо рассмотреть несколько теоретических моментов.
Теорема 1. Функция 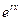 является решением линейного однородного дифференциального уравнения
является решением линейного однородного дифференциального уравнения 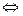
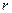 есть характеристический корень.
есть характеристический корень.
Доказательство. Ищем решение в виде 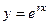 .
.
Если 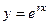 , то
, то 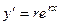 ,
, 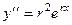 , ...
, ... 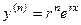 .
.
Подставим в уравнение 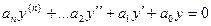 .
.
Получим 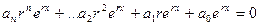 .
.
Во всех слагаемых одинаковая экспонента, вынесем её за скобку:
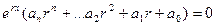 .
.
Но поскольку 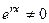 , то
, то 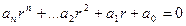 .
.
Что и требовалось доказать.
Теорема 2. Линейная комбинация решений линейного однородного дифференциального уравнения тоже является его решением.
Доказательство. (ДОК 23)
Пусть 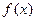 и
и 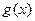 - два различных решения уравнения
- два различных решения уравнения
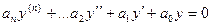 .
.
То есть, они оба обращают его в тождество:
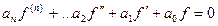 и
и
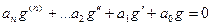 .
.
Надо доказать, что линейная комбинация 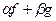 тоже подходит в качестве решения. Известно, что для производной, а также и последующих выполняется свойство линейности:
тоже подходит в качестве решения. Известно, что для производной, а также и последующих выполняется свойство линейности: 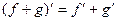 , поэтому
, поэтому 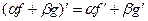 ,
, 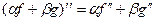 , и т.д.
, и т.д.
Тогда, подставляя линейную комбинацию в дифференциальное уравнение, получим:
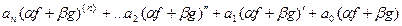 =
=
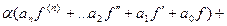
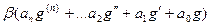
Но ведь в каждой скобке 0, так как каждая из этих функция была решением уравнения. Получается 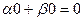 .
.
Таким образом, линейная комбинация решений тоже является решением линейного уравнения.
Задача 1. Решить уравнение 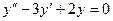 .
.
Решение. Характеристическое уравнение: 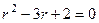 , оно сводится к виду
, оно сводится к виду 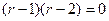 , корни
, корни 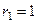 ,
, 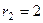 . Тогда решениями могут быть только
. Тогда решениями могут быть только 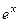 и
и 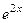 . Сделаем проверку для каждой из экспонент. Подставим каждую из них в уравнение.
. Сделаем проверку для каждой из экспонент. Подставим каждую из них в уравнение.
1) 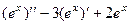 =
= 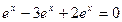 .
.
2) 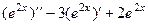 =
= 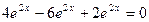 .
.
Проверка выполнена. Обе экспоненты являются решениями.
При этом никакая третья экспонента не может служить решением этого же уравнения, потому что характеристический многочлен 2-й степени, и он имеет максимум 2 корня.
Их линейная комбинация 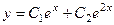 .
.
Ответ. 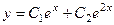 .
.
Задача 2. Найти общее решение дифф. уравнения 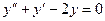 .
.
Решение. Характеристическое уравнение: 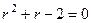 , его корни
, его корни
1 и 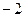 . Тогда ФСР =
. Тогда ФСР = 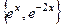 , и общее решение:
, и общее решение: 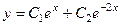 .
.
Ответ. 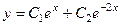 .
.
Задача 3. Найти частное решение дифф. уравнения 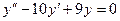 при условиях Коши:
при условиях Коши: 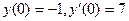 .
.
Решение. Характеристическое уравнение: 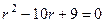 , его корни:
, его корни: 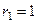 ,
, 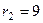 . Тогда ФСР состоит из
. Тогда ФСР состоит из 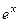 и
и  , общее решение такое:
, общее решение такое: 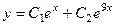 .
.
Теперь найдём решение задачи Коши. Сначала запишем функцию и её производную: 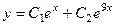 и
и 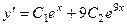 .
.
Кроме того, у нас есть информация: 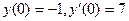 .
.
Тогда 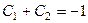 ,
, 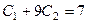 . Получается система уравнений
. Получается система уравнений
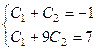 вычитая 1-е уравнение из 2-го, находим,
вычитая 1-е уравнение из 2-го, находим, 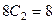 , т.е.
, т.е. 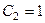 , тогда
, тогда 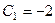 . Тогда частное решение:
. Тогда частное решение: 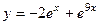 .
.
Ответ. Общее решение 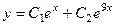 , частное
, частное 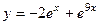 .
.
Задача 4. Решить уравнение 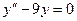 , найти частное решения для условий Коши:
, найти частное решения для условий Коши: 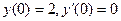 .
.
Решение. Характеристическое уравнение: 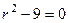 , его корни:
, его корни: 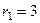 ,
, 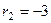 . Тогда ФСР состоит из
. Тогда ФСР состоит из 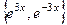 , общее решение такое:
, общее решение такое: 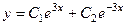 .
.
Теперь найдём решение задачи Коши. Сначала запишем функцию и её производную:
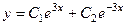 и
и 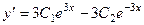 .
.
Кроме того, у нас есть информация: 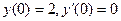 .
.
Ищем частное решение.
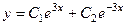 ,
, 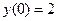
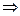
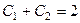
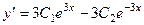 ,
, 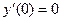
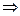
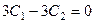
Получается система уравнений
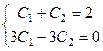 , решая её, находим из 2-го
, решая её, находим из 2-го 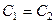 ,
,
откуда 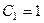 ,
, 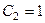 . Тогда частное решение:
. Тогда частное решение: 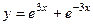 .
.
Ответ. 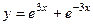 .
.
Если 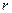 - корень кратности
- корень кратности 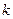 , то в системе решений будут присутствовать
, то в системе решений будут присутствовать 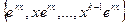 , то есть одну и ту же экспоненту
, то есть одну и ту же экспоненту 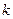 раз включать в фундаменатльную систему решений нельзя, иначе фактическое количество функций в ФСР получится меньше, чем n.
раз включать в фундаменатльную систему решений нельзя, иначе фактическое количество функций в ФСР получится меньше, чем n.
Кроме самой экспоненты, нужно взять ещё и с домножением на степенные, по нарастанию степеней до 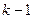 .
.
Задача 5. Решить уравнение 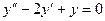 .
.
Решение. Характеристическое уравнение: 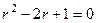 , то есть
, то есть 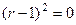 , характеристическое корни
, характеристическое корни 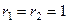 . Тогда ФСР:
. Тогда ФСР: 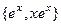 , а общее решение:
, а общее решение: 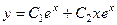 .
.
Ответ. 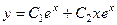 .
.
Сделаем проверку. Для 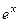 очевидно. Проверим
очевидно. Проверим 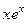 .
.
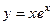 , тогда
, тогда 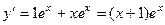 ,
, 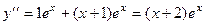 .
.
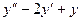 =
= 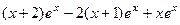 =
= 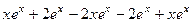 =
= 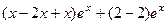 = 0.
= 0.
Если один из корней 0, то в ФСР присутствует экспонента вида 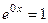 , то есть контанта 1 принадлежит ФСР.
, то есть контанта 1 принадлежит ФСР.
Задача 6. Решить уравнение 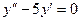 .
.
Решение. Характеристическое уравнение: 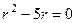 , корни 0 и 5. Тогда ФСР:
, корни 0 и 5. Тогда ФСР: 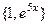 , а общее решение:
, а общее решение: 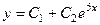 .
.
Ответ. 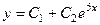 .
.
***
Ещё одно небольшое теоретическое отступление. Докажем, что если 0 является корнем кратности 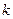 , то система решений, соответствующих этому корню, имеет вид
, то система решений, соответствующих этому корню, имеет вид 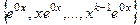 , то есть
, то есть 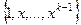 . Характеристическое уравнение обязательно имеет вид
. Характеристическое уравнение обязательно имеет вид 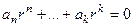 , так как
, так как 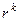 можно вынести за скобку
можно вынести за скобку 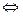 0 корень кратности
0 корень кратности 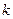 . Но это значит, что исходное дифференциальное уравнение имеет вид
. Но это значит, что исходное дифференциальное уравнение имеет вид 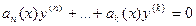 .
.
Оно содержит производные порядка 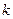 и выше. Известно, что если степенную функцию продифференцировать столько раз, какова её степень, то получим константу, а если большее количество раз, то обратится в 0. Так, например,
и выше. Известно, что если степенную функцию продифференцировать столько раз, какова её степень, то получим константу, а если большее количество раз, то обратится в 0. Так, например,
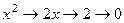 ,
, 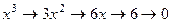 .
.
В данном уравнении производные порядка 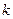 и выше. Любая из степенных функций порядка
и выше. Любая из степенных функций порядка 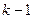 и ниже, а именно взятая из набора
и ниже, а именно взятая из набора 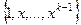 , является решением.
, является решением.
Случай комплексных корней. Если присутствуют два сопряжённых корня 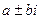 то общее решение:
то общее решение: 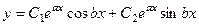 .
.
Задача 7. Найти общее решение уравнения 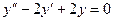 .
.
Решение. Характеристическое уравнение: 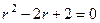 .
.
Ищем его корни. 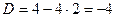 . Корни
. Корни 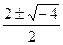 =
= 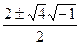 =
=
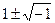 =
= 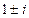 . Найдём действительную и мнимую части функции
. Найдём действительную и мнимую части функции 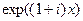 =
= 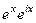 =
= 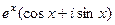 =
= 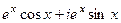 .
.
Две линейно-независимых функции образуют ФСР:
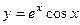 и
и 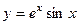 . Общее решение:
. Общее решение: 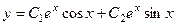 .
.
Ответ. 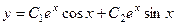 .
.
Проверка. Проверим, например, одно из слагаемых.
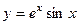
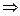
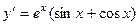
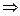
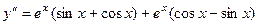 =
= 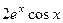 .
.
Подставим в уравнение. 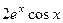
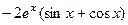
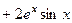 = 0.
= 0.
Задача 8. Найти общее решение уравнения 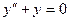 .
.
Решение. Характеристическое уравнение: 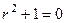 , т.е.
, т.е. 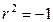 корни
корни 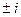 , то есть
, то есть 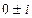 . Две линейно-независимых функции образуют ФСР:
. Две линейно-независимых функции образуют ФСР: 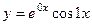 и
и 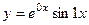 .
.
Общее решение: 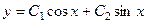 .
.
Ответ. 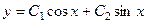 .
.
Дата: 2019-11-01, просмотров: 306.