Приходовский М.А.
Математика
Курс практических занятий
Семестр 3
Учебное пособие для специальности
Прикладная информатика в экономике»
Томск
ТУСУР
2019
Электронное учебное пособие составлено по материалам практических занятий на ФСУ в группах 448-1,2 осенью 2019 года.
Оглавление
| Линейные дифференциальные уравнения высшего порядка...... Циркуляция, формула Грина ......................................................... Потенциальные векторные поля .................................................... Действия над комплексными числами.......................................... Функции комплексного переменного............................................ Интегрирование функций комплексного переменного............... Интегральная формула Коши......................................................... Особые точки и вычеты.................................................................. | 5 15 19 25 32 44 50 59 |
Содержание по номерам задач и датам практик
| 448-1 | задачи: | 448-2 | ||
| Практика 1 | 2.9 | 1-10 | 7.9 | 1-10 |
| Практика 2 | 4.9 | 11-17 | 11.9 | 11-17 |
| Практика 3 | 9.9 | 18-27 | 14.9 | 18-27 |
| Практика 4 | 16.9 | 28-32* | 21.9 | 28-33* |
| Практика 5 | 18.9 | 33 - 44 | 25.9 | 34 - 44 |
| Практика 6 | 23.9 | 45 - 53 | 28.9 | 45 - 53 |
| Практика 7 | 30.9 | 54 - 58 * | 5.10 | 54 - 58* |
| Практика 8 | 2.10 | 59 - 66 | 9.10 | 59 - 66 |
| Практика 9 | 7.10 | 67 - 79 | 12.10 | 67 - 79 |
| Практика 10 | ||||
* на практике есть контрольная работа
Линейные неоднородные уравнения высшего порядка.
Циркуляция и формула Грина.
Задача 15.
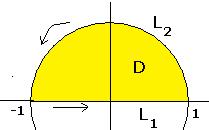
Найти циркуляцию векторного поля 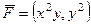 по перемещению точки по границе верхнего полукруга радиуса 1 двумя методами:
по перемещению точки по границе верхнего полукруга радиуса 1 двумя методами:
А). без формулы Грина. Б). по формуле Грина.
Решение.
Решение А). без формулы Грина. В этом случае нужно для каждого участка - отрезка  и полуокружности
и полуокружности  - вычислить работу поля отдельно. Чтобы обход всего контура осуществлялся один раз и против часовой стрелки, надо, чтобы движение по отрезку было слева направо
- вычислить работу поля отдельно. Чтобы обход всего контура осуществлялся один раз и против часовой стрелки, надо, чтобы движение по отрезку было слева направо 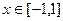 (при этом
(при этом 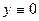 , и
, и 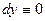 ), а по полуокружности справа налево, т.е. на ней использовать обычный метод параметрического задания точек:
), а по полуокружности справа налево, т.е. на ней использовать обычный метод параметрического задания точек:  .
.
По 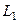 :
: 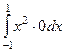 = 0.
= 0.
По 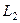 :
: 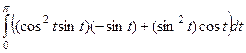 =
=
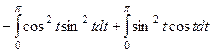 , во втором интеграле очевидно, подведение под знак дифференциала, а в первом есть несколько путей решения:
, во втором интеграле очевидно, подведение под знак дифференциала, а в первом есть несколько путей решения:
1) с помощью замены, учитывая то, что суммарная степень чётна (изучали во 2 семестре).
2) применить формулу понижения степени к каждому из квадратов.
3) использовать то, что 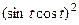 и формулу
и формулу 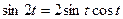 .
.
Наиболее оптимальным наверное, здесь будет 3-й путь.
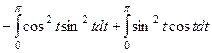 =
= 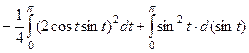
= 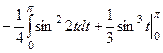 =
= 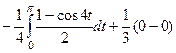 =
=
 =
= 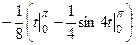 =
= 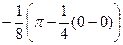 =
= 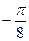 .
.
Решение Б). По формуле Грина.
Если 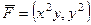 то
то 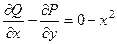 .
.
Двойной интеграл по полукругу вычисляется с помощью полярных координат, это стандартная задача, которые решали во 2 семестре. Так как полукруг в верхней полуплоскости, то 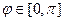 , а радиус 1,
, а радиус 1,  .
.
 =
= 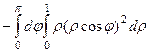 =
= 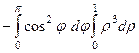 =
=
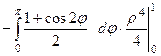 =
= 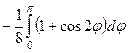 =
= 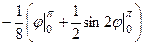 =
= 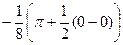 =
=  .
.
Ответ. 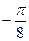 .
.
Задача 16. Найти циркуляцию векторного поля 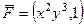 по перемещению точки по треугольнику с вершинами (0,0), (0,1), (1,1) с помощью формулы Грина.
по перемещению точки по треугольнику с вершинами (0,0), (0,1), (1,1) с помощью формулы Грина.
Решение. Если не использовать формулу Грина, то на каждой из сторон - горизонтальной, вектикальной и наклонной - надо было бы отдельно провести вычисление работы поля. Используя формулу Грина, мы вычислим лишь один двойной интеграл.
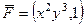
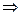
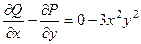 .
.
Чертёж этого треугольника:
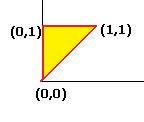
Далее следует стандартный метод вычисления двойного интеграла, изученный в прошлом семестре. Сначала спроецируем фигуру на ось Ох и найдём глобальные границы по 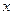 , это
, это 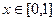 . При каждом конкретном
. При каждом конкретном 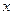 высота изменяется от наклонной линии
высота изменяется от наклонной линии 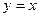 до горизонтальной
до горизонтальной 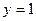 , то есть
, то есть 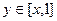 . Итак,
. Итак,
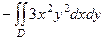 =
=  =
= 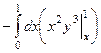 =
= 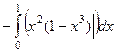 =
= 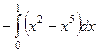 =
= 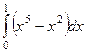 =
= 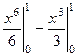 =
=  =
= 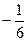 .
.
Ответ. 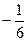 .
.
Задача 17. Найти циркуляцию векторного поля 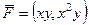 по перемещению точки по квадрату
по перемещению точки по квадрату 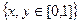 , с помощью формулы Грина.
, с помощью формулы Грина.
Решение.  ,
, 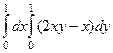 =
= 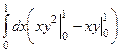 =
=  =
= 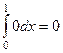 .
.
Ответ. 0.
Задача 17*. (дополнительно, или домашняя). Найти циркуляцию векторного поля 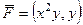 по перемещению точки по треугольнику с вершинами (0,0), (1,0), (1,1) с помощью формулы Грина.
по перемещению точки по треугольнику с вершинами (0,0), (1,0), (1,1) с помощью формулы Грина.
Ответ. 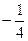 .
.
Решение.
Чтобы доказать, что поле потенциально, построим матрицу из всех 9 производных. В первом столбце по  , во втором по
, во втором по 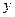 и в 3-м по
и в 3-м по  :
:
 =
= 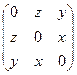
Матрица симметрична 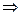 поле потенциально.
поле потенциально.
Теперь ищем потенциал. Для этого соединим начальную точку с произвольной с помощью ломаной, чтобы каждое звено было параллельно какой-либо из осей координат.

Начальная точка, как правило, (0,0,0). Изменяющуюся переменную при этом будем обозначать через 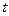 , чтобы отличать от переменных
, чтобы отличать от переменных  ,
, 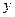 ,
,  , которые в этих вычислениях будут использять роль верхнего предела в том или ином интеграле, либо роль фиксированной константы внутри функции. Получается такая сумма интегралов:
, которые в этих вычислениях будут использять роль верхнего предела в том или ином интеграле, либо роль фиксированной константы внутри функции. Получается такая сумма интегралов:
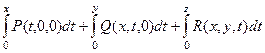
Применим это к конкретным функциям в этой задаче.
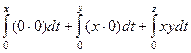 =
= 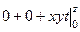 =
= 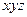 .
.
Вспомнив, что потенциал определяется с точность до константы, окончательный ответ можно записать так: 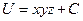 .
.
Ответ. 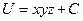 .
.
Задача 24. 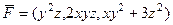 .
.
Решение. Найдём производную матрицу.
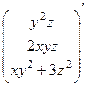 =
= 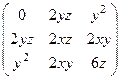
Она симметрична, значит, поле потенциально. Ищем потенциал:
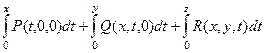 =
=
 =
= 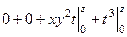 =
=  .
.
Ответ.  .
.
Задача 25. 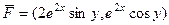 .
.
Решение.  =
= 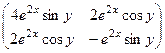 симметрична.
симметрична.
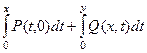 =
= 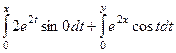 =
= 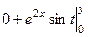 =
=  . Ответ.
. Ответ. 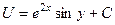 .
.
Задача 26.  .
.
Решение.  =
= 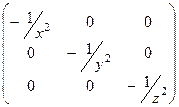 симметрична.
симметрична.
В данном случае мы не можем в качестве начальной точки взять (0,0,0), так как эти функции имеют там бесконечный предел. Однако можно рассматривать точку (1,1,1) .
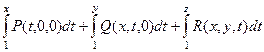 =
= 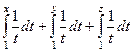 =
=
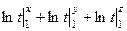 =
=  =
=
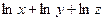 =
= 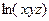 .
.
Ответ. 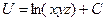 .
.
Решение.
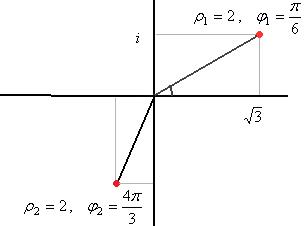
Для 1-го числа: 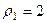 ,
, 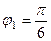 (та же точка, как в прошлой задаче).
(та же точка, как в прошлой задаче).
Для 2-го числа: 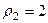 ,
, 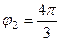 . Тогда
. Тогда 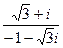 =
=  =
= 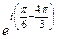 =
=  =
= 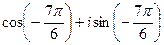 , прибавим
, прибавим 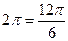 , для удобства вычисления. Итак,
, для удобства вычисления. Итак, 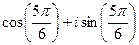 =
= 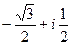 .
.
Ответ. 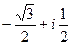 .
.
Задача 30. Вычислить  .
.
Решение. Представим в показательной форме каждое из чисел.
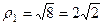 ,
, 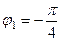 и
и 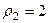 ,
, 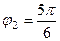 . Тогда
. Тогда
 =
= 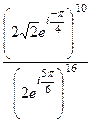 =
= 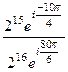 =
=  здесь в числителе прибавили угол
здесь в числителе прибавили угол 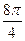 , кратный
, кратный 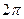 , а в знаменателе отняли
, а в знаменателе отняли 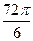 . Далее,
. Далее,  =
=  =
=  =
= 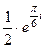 =
= 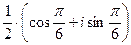 =
= 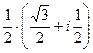 =
= 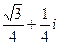 .
.
Ответ. 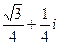 .
.
Домашняя задача. Вычислить  . Ответ.
. Ответ. 
Задача 31. Вычислить 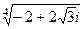
Решение. Формула: 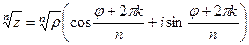 .
.
Сначала найдём модуль и аргумент исходного числа.
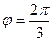 (т.к. 90 градусов и ещё 30 во второй четверти),
(т.к. 90 градусов и ещё 30 во второй четверти),
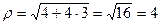 .
.
Тогда 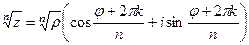 =
= 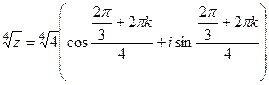 =
= 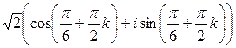 таким образом, 4 точки лежат на окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня:
таким образом, 4 точки лежат на окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня:
 :
: 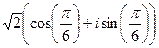 =
=  =
= 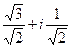 .
. 
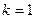 :
: 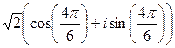 =
= 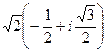 =
= 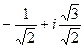 .
. 
 :
:  =
= 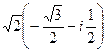 =
=  .
. 
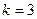 :
: 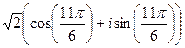 =
= 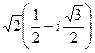 =
= 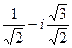 .
. 
Чертёж:
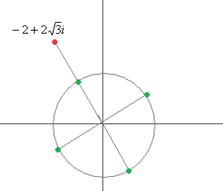
Ответ.  и
и 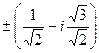 .
.
Задача 32. Дано 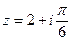 . Найти
. Найти 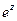 .
.
Решение. 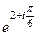 =
= 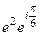 =
= 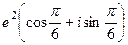 =
= 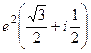 .
.
Ответ. 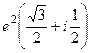 .
.
Задача 33. Дано 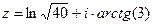 . Найти
. Найти 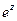 .
.
Решение. 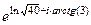 =
= 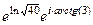 =
= 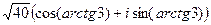 . Далее с помощью прямоугольного треугольника вычислим
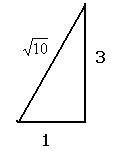
. Далее с помощью прямоугольного треугольника вычислим 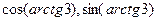 . Если надо найти синус и косинус того угла, тангенс которого равен 3, то сначала подпишем длины катетов по известному тангенсу, гипотенуза
. Если надо найти синус и косинус того угла, тангенс которого равен 3, то сначала подпишем длины катетов по известному тангенсу, гипотенуза 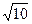 вычислится автоматом по теореме Пифагора, а далее будет уже известны синус и косинус.
вычислится автоматом по теореме Пифагора, а далее будет уже известны синус и косинус.
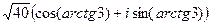 =
= 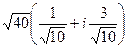 =
= 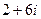 .
.
Ответ. 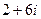 .
.
Задача 34. Дано 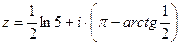 . Найти
. Найти 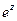 .
.
Решение. 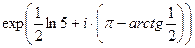 =
= 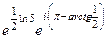 =
=
 =
=
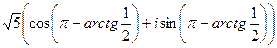 . Делаем аналогично тому, как в прошлой задаче, просто треугольник здесь во 2 четверти (угол
. Делаем аналогично тому, как в прошлой задаче, просто треугольник здесь во 2 четверти (угол 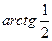 отмеряется от 180 в обратном направлении).
отмеряется от 180 в обратном направлении).

Но гипотенуза всё равно легко вычисляется по теореме Пифагора: 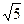 , тогда
, тогда 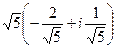 =
= 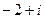 .
.
Ответ. 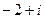 .
.
Задача 35. Найти все значения  .
.
Решение. Используем формулу 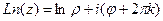 .
.
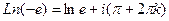 =
= 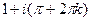 . Таким образом, это точки в комплексной плоскости, имеющие вид:
. Таким образом, это точки в комплексной плоскости, имеющие вид: 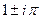 ,
, 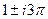 ,
,  , ...
, ...
Ответ. 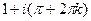 .
.
Задача 36. Вычислить 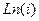 .
.
Решение. 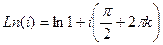 =
= 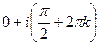 . Последовательность значений такова:
. Последовательность значений такова: 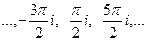 каждая соседняя пара отличается на
каждая соседняя пара отличается на 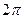 по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для
по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для 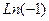 .
.
Ответ. 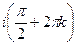 .
.
Задача 37. Найти все значения 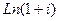 .
.
Решение. Используем формулу 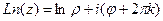 .
.
Для числа 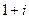 ,
,  ,
, 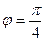 . Тогда
. Тогда
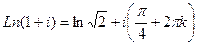 .
.
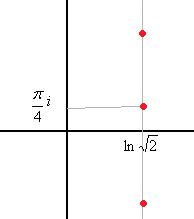
Чертёж: бесконечная последовательность точек, на уровне абсциссы
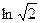 , по высоте каждая пара соседних отличается на
, по высоте каждая пара соседних отличается на 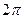 .
.
Ответ. 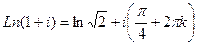 .
.
Задача 38. Вычислить 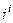 .
.
Решение. Представим 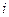 , расположенную в основании, в виде
, расположенную в основании, в виде  . Тогда
. Тогда 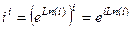 , причём чуть выше мы вычисляли
, причём чуть выше мы вычисляли
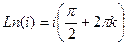 . Тогда
. Тогда 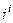 =
= 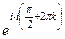 =
= 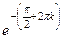 т.е. получается бесконечное множество точек на действительной оси.
т.е. получается бесконечное множество точек на действительной оси.
Ответ. 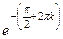 .
.
Решение.
Способ 1.
Производная как от единой функции  :
:
 =
= 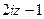 , что в точке
, что в точке 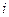 равно
равно 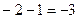 .
.
Способ 2.
По компонентам 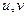 из предыдущей задачи:
из предыдущей задачи:
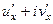 =
= 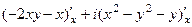 =
= 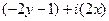 ,
,
в точке 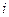 означает что в
означает что в  , т.е. данные функции надо вычислить в точке
, т.е. данные функции надо вычислить в точке 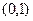 . Тогда
. Тогда 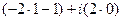 =
= 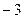 , как и том способе.
, как и том способе.
Ответ. 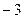 .
.
Интегральная формула Коши.
Следующая серия задач решается с помощью формул Коши:
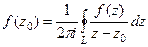 и
и 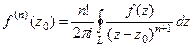 .
.
Здесь будут комбинированные задачи, состоящие из нескольких подзадач, где контур проводится сначала вокруг той или иной точки разрыва, а затем вокруг всех этих точек.
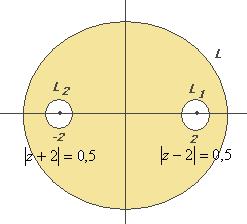
Задача 65. Вычислить 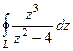 , где контур
, где контур 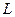 :
:
А) 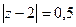 Б)
Б) 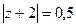 В)
В) 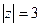 .
.
Решение. В знаменателе разложим на множители, и станет видно, что корни многочлена там 2 и 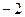 .
.
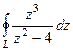 =
= 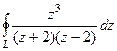 .
.
Если контур радиуса 0,5 окружает одну из точек, то надо применить интегральную формулу Коши, где точка 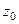 одна из них, а именно, в первом пункте
одна из них, а именно, в первом пункте 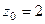 , а во втором
, а во втором 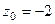 . Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное
. Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное  вместо
вместо  в оставшейся части функции.
в оставшейся части функции.
А) 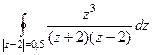 =
=  =
= 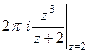 =
=  =
= 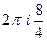 =
=  .
.
Б)  =
= 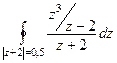 =
= 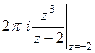 =
= 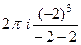 =
= 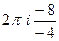 =
=  .
.
В) В третьем пункте, где контур окружает уже обе точки, достаточно будет воспользоваться теоремой Коши и суммировать результаты двух предыдущих пунктов. Получится 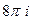 .
.
Ответы. А) 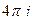 Б)
Б) 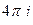 В)
В) 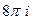 .
.
Задача 66. Вычислить 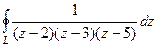 , где контур
, где контур 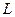 :
:
А) 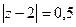 Б)
Б) 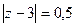 В)
В) 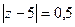 Г)
Г) 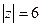 Д)
Д) 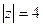 .
.
Решение. В каждом случае применяем интегральную формулу Коши к той или иной точке разрыва функции, 2, 3 и 5. Убирая соответствующий множитель из знаменателя, затем подставляем в оставшуюся часть функции это число.
А) 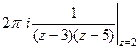 =
= 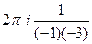 =
= 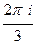 .
.
Б)  =
= 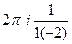 =
= 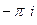 .
.
В)  =
= 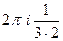 =
= 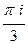 .
.
Если радиус 6, то все 3 точки находятся внутри контура. Суммируем все 3 результата:
Г) 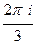
 +
+  = 0 .
= 0 .
В последнем случае, лишь две из трёх точек внутри контура:
Д) 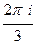
 =
= 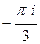 .
.
Ответы. А) 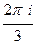 Б)
Б) 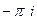 В)
В)  Г) 0 Д)
Г) 0 Д) 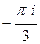 .
.
Задача 67. Вычислить 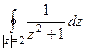 .
.
Решение. 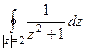 =
= 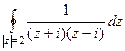 . Здесь две особые точки, это
. Здесь две особые точки, это  , они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.
, они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.
 =
= 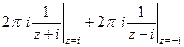 =
=
 =
= 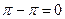 .
.
Ответ. 0.
Задача 68. Вычислить 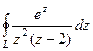 , где контур
, где контур 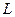 :
:
А) 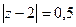 Б)
Б)  В)
В) 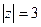 .
.
Решение. В 1 пункте здесь корень 2 соответствует 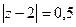 , а во втором корень 0, но он имеет кратность 2, поэтому надо будет сделать по обобщённой интегральной формуле Коши, то есть с помощью производной.
, а во втором корень 0, но он имеет кратность 2, поэтому надо будет сделать по обобщённой интегральной формуле Коши, то есть с помощью производной.
А) 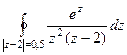 =
= 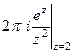 =
= 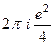 =
=  .
.
Б) Здесь корень 0, он соответствует множителю  , который, впрочем, можно было бы записать в виде скобки
, который, впрочем, можно было бы записать в виде скобки 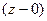 .
.
Конкретизируем обобщённую формулу Коши для 2 степени:
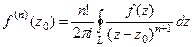 , при n=1:
, при n=1: 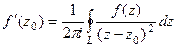
Тогда 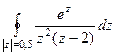 =
= 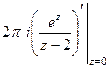 =
= 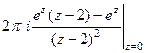 =
=
 =
= 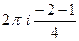 =
= 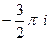 .
.
В) Здесь внутри контура обе особые точки, рассмотренные в предыдущих пунктах. По интегральной теореме Коши просто складываем результаты, полученные в 2 предыдущих пунктах. Получаем 
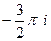 .
.
Ответы. А)  Б)
Б) 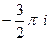 В)
В) 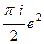
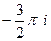 .
.
Задача 69. Вычислить 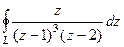 , где контур
, где контур 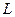 :
:
А) 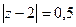 Б)
Б) 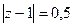 В)
В) 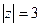 .
.
Решение.
А) 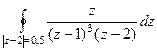 =
= 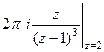 =
=  =
=  .
.
Б) В этом случае корень знаменателя имеет кратность 3, так что придётся считать с помощью 2-й производной.
Конкретизируем обобщённую формулу Коши для 3 степени:
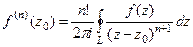 , при n=2:
, при n=2: 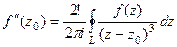 . Тогда
. Тогда 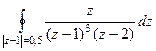 =
= 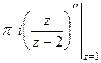 =
=
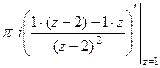 =
= 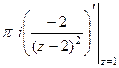 =
= 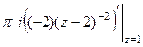 =
= 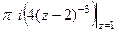 =
=  =
= 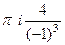 =
=  .
.
В) 
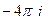 = 0 .
= 0 .
Ответы. А) 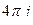 Б)
Б) 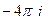 В) 0 .
В) 0 .
Задача 70. Вычислить 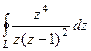 , где контур
, где контур 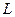 :
:
А) 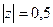 Б)
Б) 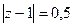 В)
В) 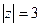 .
.
Решение.
А) 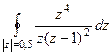 =
= 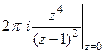 =
=  = 0.
= 0.
Б) 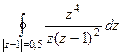 =
= 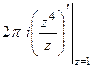 =
= 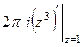 =
= 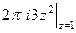 =
= 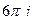 .
.
В) 0+ 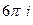 =
= 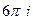 .
.
Ответы. А) 0 Б) 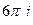 В)
В) 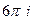 .
.
Задача 71. Вычислить 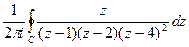 , где контур
, где контур 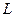 :
:
А) 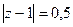 Б)
Б) 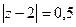 В)
В) 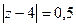 Г)
Г) 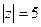 .
.
Решение. Так как здесь в интеграле уже изначально есть множитель 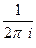 , то домножать на
, то домножать на 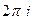 в правой части не нужно.
в правой части не нужно.
А)  =
= 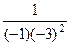 =
= 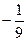 .
.
Б) 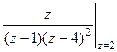 =
=  =
= 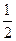 .
.
В) В отличие от двух первых точек, здесь в знаменателе корень 2-го порядка, поэтому подставляем 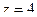 не сразу, а после вычисления производной.
не сразу, а после вычисления производной.
 =
=  =
= 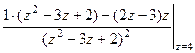 =
= 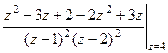 =
= 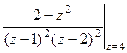 =
= 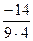 =
= 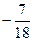 .
.
Г) По интегральной теореме Коши, сумма интегралов по трём предыдущим контурам: 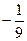 +
+ 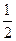
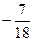 = 0 .
= 0 .
Ответы. А) 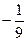 Б)
Б) 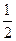 В)
В) 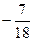 Г) 0.
Г) 0.
Задача 72. Вычислить 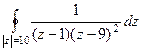 .
.
Решение. Здесь две особые точки, 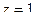 полюс 1-го порядка и
полюс 1-го порядка и  полюс 2-го порядка. Для 2-й точки надо применять обобщённую формулу Коши (с производной).
полюс 2-го порядка. Для 2-й точки надо применять обобщённую формулу Коши (с производной).
 =
=  =
=
 =
= 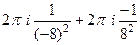 =
=
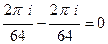 .
.
Ответ. 0.
Задача 73. Вычислить 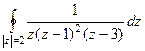 .
.
Решение. Внутри окружности радиуса 2 лежат 2 из 3 особых точек, а именно, 0 и 1, точка 3 снаружи.
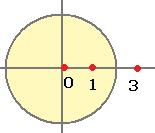
Поэтому интегральную формулу Коши применяем только к двум точкам.
 =
=  .
.
Предварительно вычислим производную.
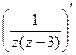 =
= 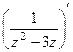 =
= 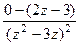 =
= 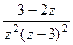 .
.
Далее, 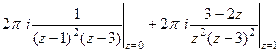 =
=
 =
= 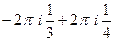 =
=
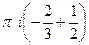 =
= 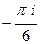 .
.
Ответ.  .
.
Задача 74. Вычислить  .
.
Решение. Здесь степень множителя в знаменателе равна 2. Есть всего одна точка разрыва, а именно 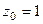 . Конкретизируем обобщённую интегральную формулу Коши для этого случая.
. Конкретизируем обобщённую интегральную формулу Коши для этого случая.
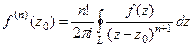 , при n = 1 получается
, при n = 1 получается
 =
= 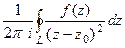 .
.
Отсюда следует, что 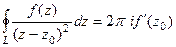
Тогда  =
= 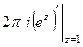 =
=  =
= 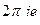 .
.
Ответ. 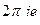 .
.
Задача 74-Б. Вычислить 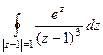 .
.
Решение. Здесь степень множителя в знаменателе равна 3. Есть всего одна точка разрыва, а именно 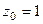 .
.
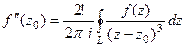 =
= 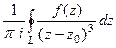 .
.
Отсюда следует, что 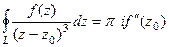
Тогда 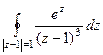 =
= 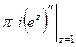 =
= 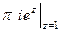 =
= 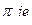 .
.
Ответ. 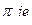 .
.
Задача 75. Вычислить 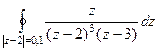 .
.
Решение. 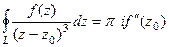 , тогда
, тогда 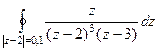 =
= 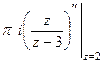 =
= 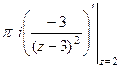 =
=  =
= 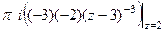 =
= 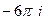
Ответ. 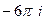 .
.
Особые точки и вычеты.
Задача 76. Найти все особые точки и определить их тип для функции 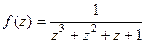 .
.
Решение. Здесь нужно сначала преобразовать выражение в знаменателе, выделить множители, соответствующие каждому корню.
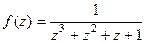 =
= 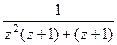 =
= 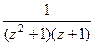 =
=  . Таким образом, полюсы 1-го порядка:
. Таким образом, полюсы 1-го порядка: 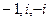 .
.
Ответ. Полюсы 1-го порядка: 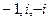 .
.
Задача 77. Найти все особые точки и определить их тип для функции  .
.
Решение. Разложим знаменатель на множители, предварительно найдём корни с помощью дискриминанта.
 =
=  =
= 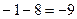 .
. 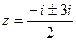 , корни
, корни 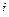 ,
,  .
.
Тогда 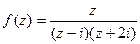 . Для знаменателя
. Для знаменателя 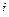 и
и 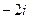 нули порядка 1, значит, для функции это полюсы порядка 1.
нули порядка 1, значит, для функции это полюсы порядка 1.
Ответ. Полюсы 1-го порядка: 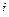 ,
,  .
.
Задача 78. Найти все особые точки и определить их тип для функции 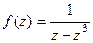 .
.
Решение. Разложим знаменатель на множители,
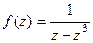 =
=  =
= 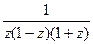 .
.
При  ,
,  ,
,  нули 1-го порядка в знаменателе, тогда для функции это полюсы 1 порядка.
нули 1-го порядка в знаменателе, тогда для функции это полюсы 1 порядка.
Ответ. Полюсы 1-го порядка: 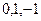 .
.
Задача 79. Исследовать тип особой точки 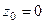 для
для  .
.
Решение. Здесь в знаменателе 3-я степень, но в этой точке в числителе тоже 0, и он влияет на итоговый порядок полюса. Надо в числителе разложить в ряд, чтобы остались одни лишь только степенные функции, потом вынесем за скобку минимальную степень, и это будет определять порядок нуля в числителе.
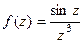 =
= 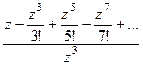 =
= 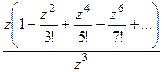
В числителе и знаменателе нули соответственно 1-го и 3-го порядка. После сокращения на 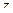 видно, что полюс 2 порядка, так как в скобках осталась функция, не стремящаяся к 0 в
видно, что полюс 2 порядка, так как в скобках осталась функция, не стремящаяся к 0 в 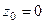 .
.
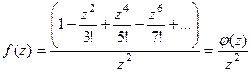 .
.
Ответ. 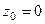 полюс 2 порядка.
полюс 2 порядка.
Приходовский М.А.
Математика
Курс практических занятий
Семестр 3
Учебное пособие для специальности
Дата: 2019-11-01, просмотров: 288.