Сначала возьмём то же самое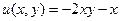 
, что в недавно сделанной задаче 47, и восстановим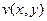 
Задача 49. Дано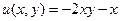 
, 
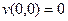. Найти 
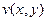и 
.
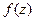Решение. Сначала проверим уравнение Лапласа
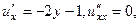
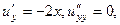в сумме 0.
Их сумма равна 0. Уравнение Лапласа выполняется. Поэтому данная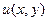 
может являться одной из компонент какой-либо комплексной функции. Далее надо вычислить 
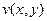, найдём её в виде потенциала от её градиента: 
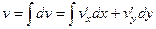то есть в виде потенциала векторного поля 
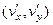. Дело в том, что в такой записи можно заменить производные от неизвестной функции 
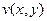на производные от известной функции 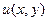по условиям Коши-Римана. 
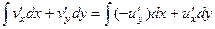. А первые производные от 
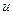уже известны, мы их вычисляли выше в процессе проверки уравнения Лапласа. Как и при вычислении потенциала, в качестве начальной точки как правило, принимаем (0,0) и интегрируем по ломаной.
= 
= 
=
= 
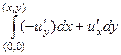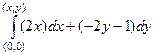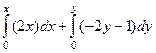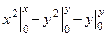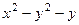, а так как начальная точка (0,0) быра взята произвольно, могла быть и иная точка, то надо зхаписать с точностью до константы: 
.
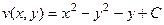При этом, если дан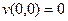о 
, то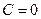 
. Итак,
.
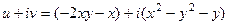Осталось восстановить функцию 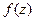. Для этого вспомним, что:
, 
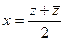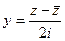
и применим эти выражения в записи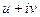 
.
=
=
=
= 
=
= 
=
= 
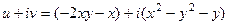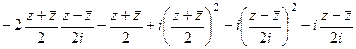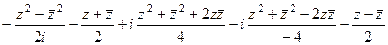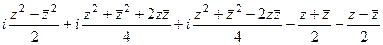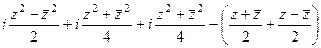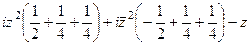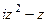
Ответ.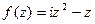 
.
Задача 50.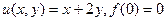 
. Найти 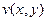и 
.
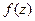Решение. Проверим уравнение Лапласа.
, 
.
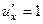
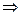
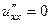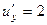
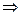
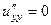Сумма вторых производных равна 0.
Ищем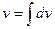 
= 
= 
= 
= 
= 
= 
.
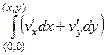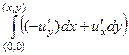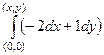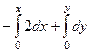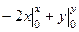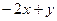При произвольном выборе начальной точки,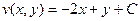 
, из условия 
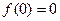определим константу 
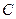. Если 
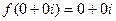то 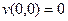, тогда 
.
= 
= 
= 
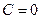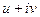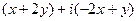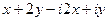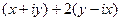. Здесь можно даже не пользоваться формулами 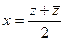, , 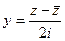ведь мы уже сумели получить 
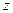в первой скобке, а во 2-й 
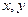в обратном порядке и одна с минусом, если домножить и поделить на 
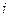, то также удастся получить выражение с 
.
= 
= 
= 
= 
= 
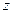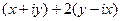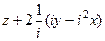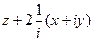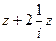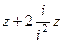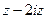. Ответ. 
.
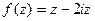Задача 51. Дано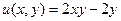 
, 
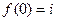. Найти 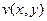и 
.
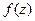Решение. Сначала проверим уравнение Лапласа, т.е. что сумма вторых производных равна 0.
,
.
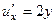
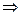
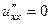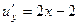
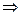
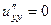Их сумма равна 0. Уравнение Лапласа выполняется.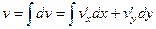 
= 
=
= 
= 
=
= 
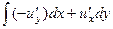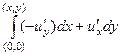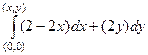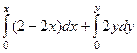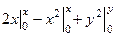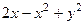. Но так как начальная точка была взята произвольно, то надо записать в самом общем виде:
.
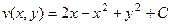При этом константа 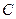должна быть такая, чтобы обеспечивалось равенство 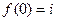, т.е. 
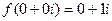, т.е. в точке 
было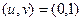 
, таким образом, должно быть 
.
.
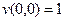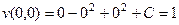
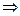
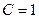Итак,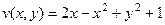 
.
Осталось восстановить функцию 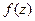. Для этого вспомним, что:
, 
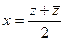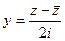
и применим эти выражения в записи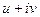 
.
= 
=
=
=
=
=
= 
.
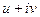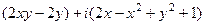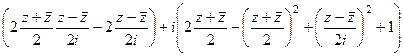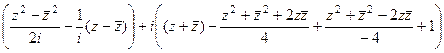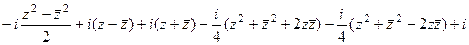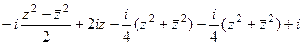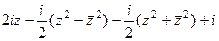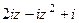Как видим,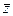 
здесь в процессе преобразований полностью сократилось. Так и должно было быть, ведь
Ответ.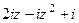 
.
Задача 52.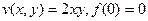 
. Найти 
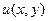и .
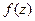Решение. Проверим уравнение Лапласа.
, 
.
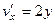
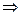
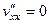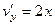
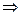
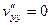Сумма вторых производных равна 0.
Ищем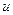 
в виде потенциала от её же градиента.
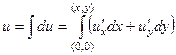где заменяем производные от неизвестной функции на производные от известной ( 
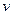) по условиям Коши-Римана.
= 
= 
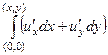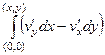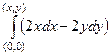
А первые производные от 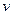мы уже считали, когда проверяли уравнение Лапласа, их и используем здесь.
= 
= 
= 
.
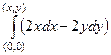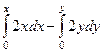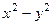Но если бы мы выбрали не (0,0) а другую начальную точку, то могло получиться и выражение с какой-то лишней константой, например если (1,2) то было бы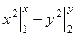 
= 
= 
.
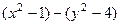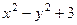Поэтому мы должны записать самый общий случай:
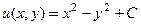, а затем уже из условия 
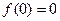определим константу 
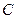. Если 
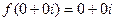то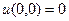 
, тогда 
.
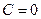Итак,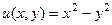 
.
Теперь запишем =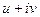 
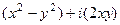и выразим все 
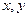через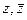 
в виде 
, 
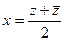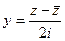. Если привести подобные, то 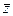сократится. 
= 
=
= 
= 
= 
.
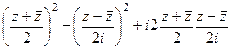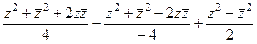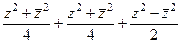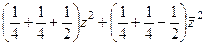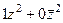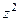Ответ.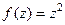 
.
Задача 53.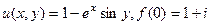 
. Найти 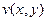и 
.
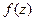Решение. Сначала проверим уравнение Лапласа.
,
.
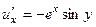
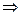
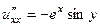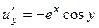
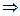
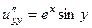Их сумма равна 0, уравнение Лапласа выполняется, 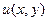- одна из компонент комплексной функции.
= 
= 
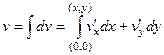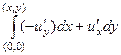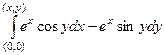
далее по ломаной интеграл вида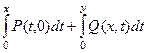 
= 
= 
=
= 
.
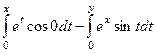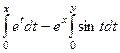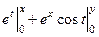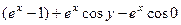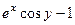В общем виде, потенциал равен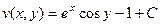 
.
Условие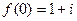 
означает 
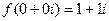и сводится к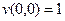 
.
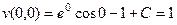
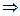
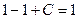
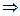
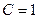Тогда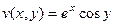 
.
Итак, =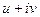 
= 
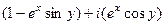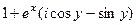. Далее на примере этой задачи мы увидим, что не обязательно использовать выражения 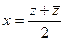, , 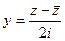можно просто сгруппировать слагаемые так, чтобы свернуть их по формуле Эйлера.
В выражении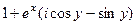 
надо получить структуру 
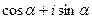, для этого внутри скобки поделим на 
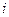а снаружи домножим.
= 
= 
=
= 
= 
.
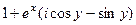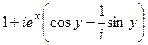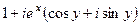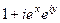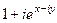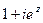Ответ.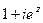 
.
Задача 54.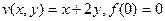 
. Найти 
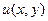и 
.
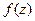Решение. Проверим уравнение Лапласа.
, 
.
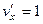
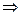
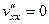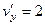
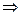
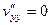Сумма вторых производных равна 0.
Ищем .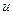 
= 
= 
=
= 
= 
.
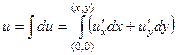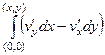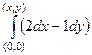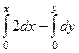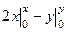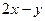При произвольном выборе начальной точки,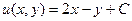 
, из условия 
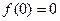определим константу 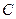. Если 
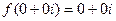то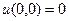 
, тогда 
.
= 
= 
=
= 
.
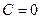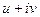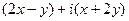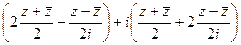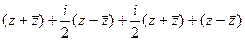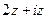Объединяя 2 крайних и 2 средних слагаемых, получаем .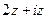
Ответ.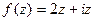 
.
Дата: 2019-11-01, просмотров: 216.
