Если правая часть неоднородного уравнения имеет вид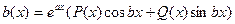 
то частное решение существует в виде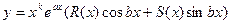 
,
где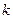 
это кратность числа 
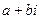в качестве характеристического корня. Если оно не является корнем, то 
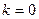. Тогда домножение происходит на 
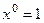, то есть фактически, не происходит.
Если в правой части нет тригонометрических функций, то всегда может автоматически считаться, что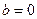 
, то есть
= 
.
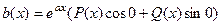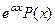Если отсутствует многочлен, а просто есть экспонента, то можем считать, что многочлен просто равен константе 1, то есть формально он всё равно есть, нулевой степени. Тогда в структуре частного решения записывается «произвольный» многочлен 0 степени, то есть константа А.
Для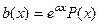 
частное решение в виде 
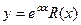, если 
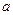не является характеристическим корнем, либо 
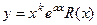, если 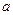совпадает с каким-то характеристическим корнем кратности .
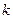Задача 9. Решить уравнение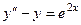 
.
методом неопределённых коэффициентов.
Решение. Шаг I. Сначала решим однородное уравнение 
.
Характеристическое: 
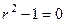, корни 1 и 
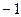. ФСР: 
.
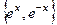Общее решение однородного: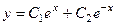 
.
Шаг II. Решаем неоднородное.
Однородное уже решено: 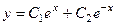. Ищем частное решение неоднородного по виду правой части.
.
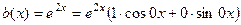Число 2 не входит в состав корней левой части, то есть кратность совпадения 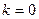. Тогда частное решение ищется в виде
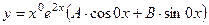, т.е. 
.
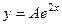Тогда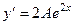 
, 
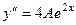. Подставим их в неоднородное уравнение.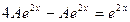 
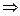
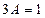
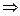
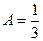
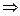частное решение неоднородного 
.
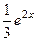Ответ.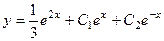 
.
Задача 10. Решить уравнение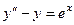 
.
методом неопределённых коэффициентов.
Решение. Шаг I. Сначала решим однородное уравнение .
Характеристическое: 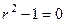, корни 1 и 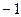. ФСР: .
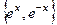Общее решение однородного: .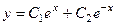
Шаг II. Решаем неоднородное.
.
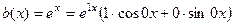Число 1 не входит в состав корней левой части, совпадая с одним из двуз корней, кратность совпадения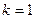 
. Тогда частное решение ищется в виде
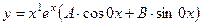, т.е. 
.
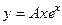Тогда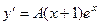 
, 
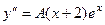. Подставим их в неоднородное уравнение.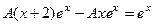 
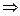
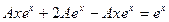
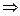
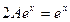
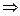
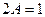
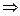
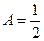
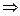частное решение неоднородного уравнения 
.
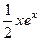Ответ.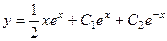 
.
Задача 11. Уравнение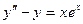 
решить методом неопределённых коэффициентов.
Решение. Общее решение однородного: .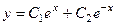
Правая часть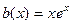 
. Экспонента степени 1, и точно такой же характеристический корень есть в левой части, он там кратности 1. Поэтому 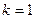, то есть в частном решении есть добавочный множитель 
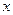. А вот вместо многочлена 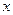, который был в правой части, надо поставить произвольный многочлен 1 степени, записав его в виде 
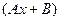. Итак, 
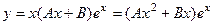. Найдём 1 и 2 производную и подставим в неоднородное уравнение.
= 
.
.
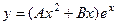
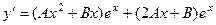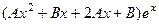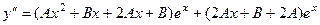Итак, из 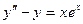следует
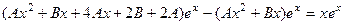, сократим на экспоненту и приведём подобные.
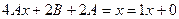, откуда 
, 
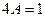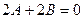, из чего следует 
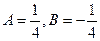. Тогда запишем частное решние приэтих значениях неопределённых коэффициентов, и добавим общее решение однородного с 1-го шага. Итак,
Ответ.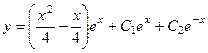 
Задача 12. Решить уравнение: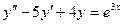 
методом неопределённых коэффициентов.
Решение. Шаг 1. Сначала найдём решение соответствующего однородного уравнения 
. Характеристическое уравнение 
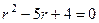, его корни 1 и 4. Их можно было как найти через дискриминант, так и просто заметить, что многочлен представляется в виде 
.
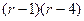Тогда общее решение однородного уравнения: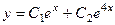 
.
Шаг 2. Заметим, что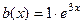 
, число 3 не является характеристическим корнем, т.е. экспонента в правой части не совпадает ни с одной из экспонент, присутствующих в решении однородного уравнения. Тогда кратность 
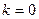, то есть дополнительный множитель в частном решении имеет вид 
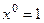, то есть фактически, его не будет. Многочлен нулевой степени, а именно 1, должны заменить на произвольный многочлен той же степени, то есть константу 
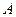. Итак, структура частного решения будет иметь вид 
. Если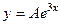 
, то легко установить, что 
, 
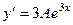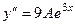. Подставим их в исходное неоднородное уравнение 
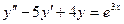. Получим 
,
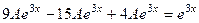то есть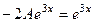 
, откуда 
, 
.
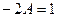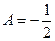Частное решение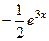 
. Тогда ответ, то есть общее решение неоднородного уравнения: 
.
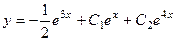Ответ.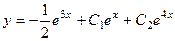 
.
В следующих 2 задачах будем варьировать правую часть по сравнению с прошлой задачей, и посмотрим, чем будет отличаться решение. Пусть там будет или умножение на степенную, или другая степень экспоненты.
Задача 13. Решить уравнение: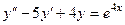 
методом неопределённых коэффициентов.
Решение. Характеристическое уравнение 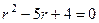, его корни 1 и 4. Общее решение однородного уравнения: 
.
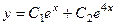Шаг 2.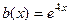 
, где 4 является характеристическим корнем. Тогда 
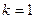. Частное решение ищется в виде 
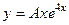. Лишний множитель 
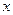из-за того, что .
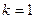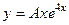
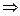
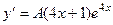
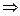
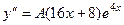
Подставим в неоднородное уравнение.
.
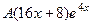
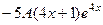
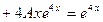
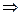
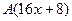
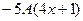
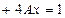
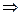
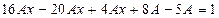
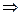
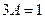
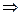
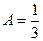Ответ.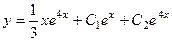 
.
Задача 14. Решить уравнение: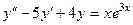 
методом неопределённых коэффициентов.
Решение. Характеристическое уравнение 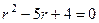, его корни 1 и 4. Общее решение однородного уравнения: 
.
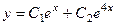Шаг 2.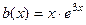 
, где 3 не является характеристическим корнем, Тогда 
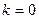, Многочлен первой степени должны заменить на произвольный многочлен той же степени, то есть 
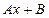. Итак, структура частного решения будет иметь вид 
.
.
= 
.
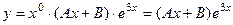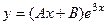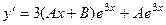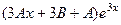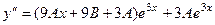
. Подставим их в исходное неоднородное уравнение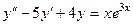 
. , там сразу можно сократить на 
.
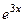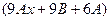
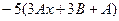
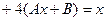
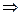
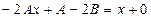
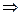система уравнений:
, 
.
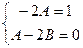
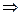
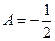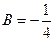Частное решение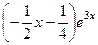 
. Тогда ответ, то есть общее решение неоднородного уравнения: 
.
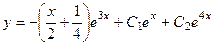Ответ.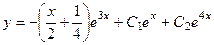 
.
Циркуляция и формула Грина.
Задача 15.
Найти циркуляцию векторного поля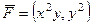 
по перемещению точки по границе верхнего полукруга радиуса 1 двумя методами:
А). без формулы Грина. Б). по формуле Грина.
Решение.
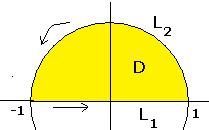
Решение А). без формулы Грина. В этом случае нужно для каждого участка - отрезка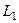 
и полуокружности 
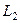- вычислить работу поля отдельно. Чтобы обход всего контура осуществлялся один раз и против часовой стрелки, надо, чтобы движение по отрезку было слева направо 
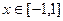(при этом 
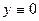, и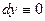 
), а по полуокружности справа налево, т.е. на ней использовать обычный метод параметрического задания точек: 
.
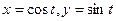По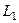 
: 
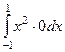= 0.
По :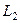 
=
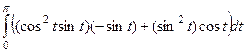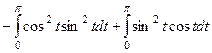, во втором интеграле очевидно, подведение под знак дифференциала, а в первом есть несколько путей решения:
1) с помощью замены, учитывая то, что суммарная степень чётна (изучали во 2 семестре).
2) применить формулу понижения степени к каждому из квадратов.
3) использовать то, что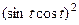 
и формулу 
.
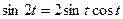Наиболее оптимальным наверное, здесь будет 3-й путь.
= 
= 
= 
=
= 
= 
= 
.
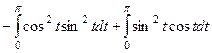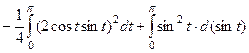
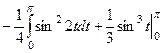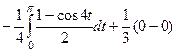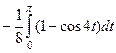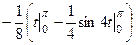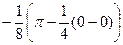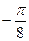Решение Б). По формуле Грина.
Если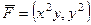 
то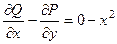 
.
Двойной интеграл по полукругу вычисляется с помощью полярных координат, это стандартная задача, которые решали во 2 семестре. Так как полукруг в верхней полуплоскости, то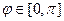 
, а радиус 1, 
.
= 
= 
=
= 
= 
= 
= 
.
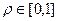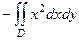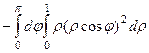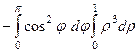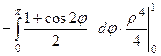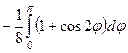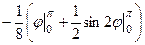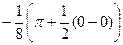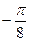Ответ. .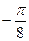
Задача 16. Найти циркуляцию векторного поля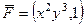 
по перемещению точки по треугольнику с вершинами (0,0), (0,1), (1,1) с помощью формулы Грина.
Решение. Если не использовать формулу Грина, то на каждой из сторон - горизонтальной, вектикальной и наклонной - надо было бы отдельно провести вычисление работы поля. Используя формулу Грина, мы вычислим лишь один двойной интеграл.
.
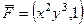
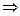
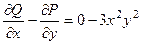Чертёж этого треугольника:
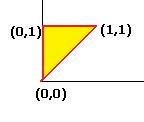
Далее следует стандартный метод вычисления двойного интеграла, изученный в прошлом семестре. Сначала спроецируем фигуру на ось Ох и найдём глобальные границы п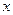о , это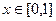 
. При каждом конкретном 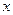высота изменяется от наклонной линии 
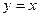до горизонтальной 
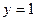, то есть 
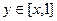. Итак,
= 
= 
= 
= 
= 
= 
= 
= 
.
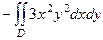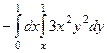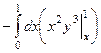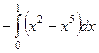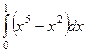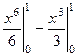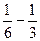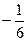Ответ. .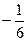
Задача 17. Найти циркуляцию векторного поля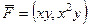 
по перемещению точки по квадрату 
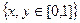, с помощью формулы Грина.
Решение. 
, 
= 
= 
= 
.
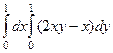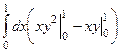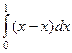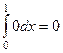Ответ. 0.
Задача 17*. (дополнительно, или домашняя). Найти циркуляцию векторного поля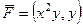 
по перемещению точки по треугольнику с вершинами (0,0), (1,0), (1,1) с помощью формулы Грина.
Ответ.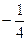 
.
Дата: 2019-11-01, просмотров: 236.
