Задача 39. Вычислить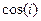 
.
Решение. Применяем формулу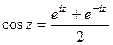 
, где аргумент вместо 
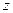подставим 
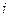. Тогда 
= 
= 
.
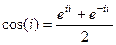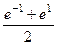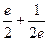Ответ. .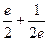
Заметим, что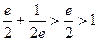 
, то есть модули значений косинуса вне действительной оси не ограничены отрезком 
.
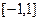Задача 40. Решить уравнение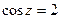 
.
Решение.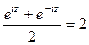 
.
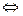
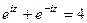
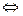
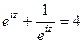Введём замену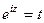 
, при этом получаем
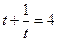
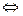
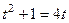
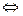
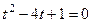. Задача разбивается на 2 шага
1) решим это уравнение и найдём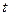 
,
2) учитывая 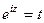, запишем 
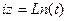и далее найдём 
.
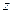Квадратичное уравнение решаем через дискриминант, здесь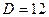 
, тогда 
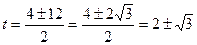. Оба значения 
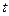- положительные действительные числа, т.е. им соответствует аргумент 
.
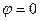Далее,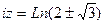 
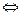
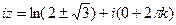
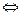
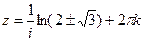
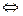
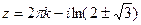. Это две бесконечных последовательности точек, одна выше а другая ниже действительной прямой. По горизонтали расстояние между соседними ровно 
.
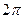Чертёж:
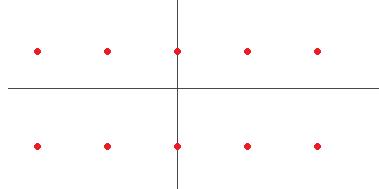
Замечание. Если число в правой части уменьшать до 1, то обе эти последовательности сближаются и в итоге соединятся в одну, расположенную на действительной прямой. Это будут в таком случае уже давно знакомые решения равенства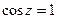 
, т.е. 
.
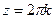Общий случай. Если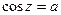 
то 
, 
, 
. То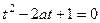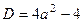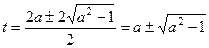гда 
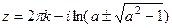, что при 
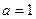порождает 
.
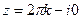В следующей серии задач надо функцию представить в виде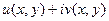 
, проверить, выполняются ли условия Коши-Римана.
Задача 41. Функцию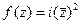 
представить в виде 
.
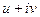Решение. =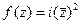 
= 
=
= 
= 
.
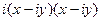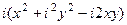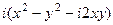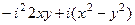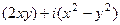Поэтому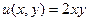 
, 
.
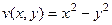Заметим, что здесь нарушено уже даже 1-е условие Коши-Римана:
, 
.
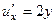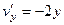Ответ.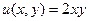 
, .
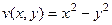Задача 42.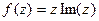 
представить в виде .
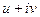Решение.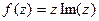 
= 
= 
, 
.
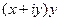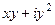
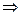
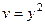Заметим, что условия Коши-Римана не выполнены, даже 1-е:
, 
.
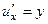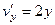Ответ. , .
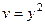Задача 43.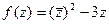 
представить в виде 
.
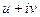Решение. =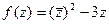 
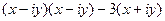
Раскроем скобки и перегруппируем слагаемые, чтобы сначала шли именно те, в которых нет мнимой единицы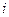 
, а затем те, в которых она есть.
= 
=
. 
.
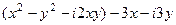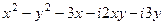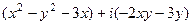
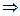
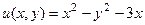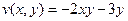Условия Коши-Римана не выполняются, даже 1-е из них:
. 
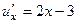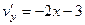, они противоположны, а должны совпадать.
Ответ.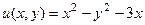 
. 
.
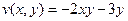Задача 44.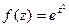 
представить в виде .
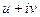Решение.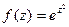 
= 
= 
= 
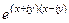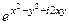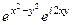
Далее по формуле Эйлера =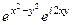 
=
.
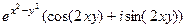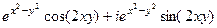Проверим выполнение условий Коши-Римана.
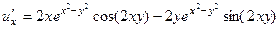
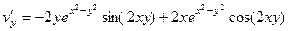
Они совпадают (1-е условие Коши-Римана).
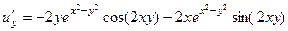
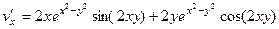
Они противоположны (2-е условие Коши-Римана).
Ответ.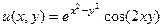 
, 
.
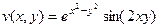Задача 45.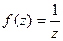 
представить в виде 
.
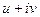Решение. =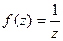 
= 
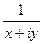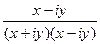
Домножили на сопряжённое, чтобы в знаменателе получилось некое единое действительное число, а разбиение на Re и Im осталось только в числителе. Тогда дробь можно будет разбить на сумму или разность двух дробей.
= 
= 
,
, 
.
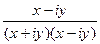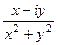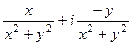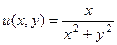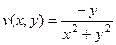Ответ.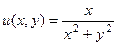 
, .
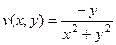Задача 46.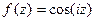 
представить в виде .
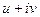Решение. Если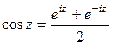 
, то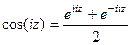 
=
= 
= 
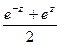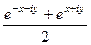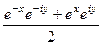
далее раскроем по формуле Эйлера:
... = 
=
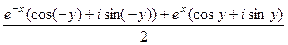воспользуемся чётностью косинуса и нечётностью синуса:
... = 
=
=
= 
,
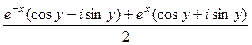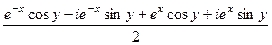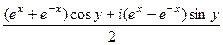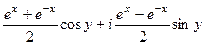это можно ещё записать в таком виде, используя гиперболические синус и косинус: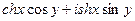 
.
Ответ.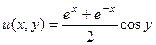 
, 
.
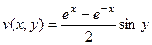Задача 47.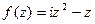 
представить в виде .
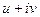Решение. =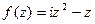 
=
= 
=
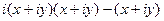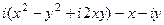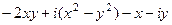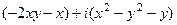, тогда
, 
.
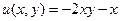Ответ. ,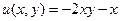 
.
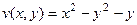Задача 48. Для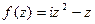 
найти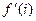 
.
Решение.
Способ 1.
Производная как от единой функции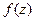 
:
= 
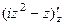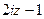, что в точке 
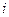равно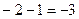 
.
Способ 2.
По компонентам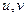 
из предыдущей задачи:
= 
= 
,
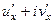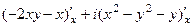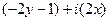в точке 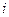означает что в 
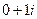, т.е. данные функции надо вычислить в точке 
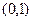. Тогда 
= 
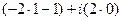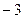, как и том способе.
Ответ. .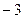
Дата: 2019-11-01, просмотров: 245.
