Рассмотрим ещё один метод решения дифференциальных уравнений, основанный на использовании потенциала поля. Пусть дано дифференциальное уравнение вида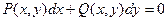 
,
причем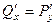 
. Тогда это уравнение называется «уравнением в полных дифференциалах». Здесь 
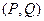является потенциальным векторным полем. В этом случае уравнение можно представить в виде 
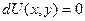, а значит, 
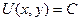. Затем остаётся только выразить 
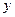через 
.
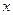Задача 27. Решить дифференциальное уравнение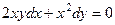 
.
Решение. Проверяем тип уравнения. Здесь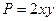 
, 
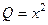. При этом
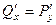, ведь 
, 
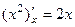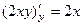. То есть, векторное поле 
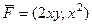потенциально. Ищем потенциал. Соединяем точки (0,0) и 
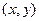с помощью ломаной, и вычисляем:
= 
= 
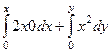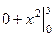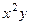. Итак, 
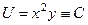. Тогда 
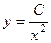общее решение дифф. уравнения.
Ответ.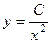 
.
Глава 2. Теория функций комплексного переменного.
Действия над комплексными числами.
Задача 28. Возвести в степень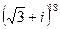 
.
Решение. Чертёж:
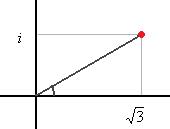
Катеты имеют длину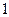 
и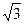 
, поэтому в полярных коорданатах:
, 
.
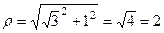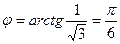Тогда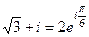 
в показательной форме, а тогда =
= 
= 
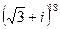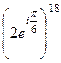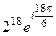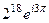далее раскроем по формуле Эйлера: 
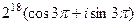, но синус и косинус не зависят от добавления и вычитания полного оборота 
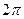, поэтому получается 
= 
= 
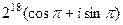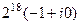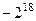. Ответ. .
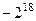Задача 29. Вычислить в показательной форме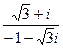 
.
Решение.
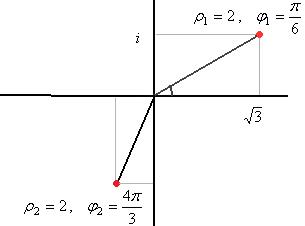
Для 1-го числа: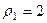 
, 
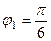(та же точка, как в прошлой задаче).
Для 2-го числа: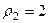 
, 
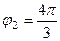. Тогда = 
= 
= 
= 
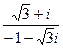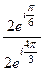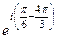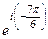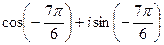, прибавим 
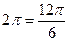, для удобства вычисления. Итак, 
= 
.
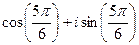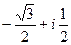Ответ.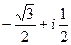 
.
Задача 30. Вычислить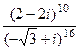 
.
Решение. Представим в показательной форме каждое из чисел.
, 
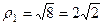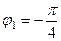и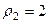 
, 
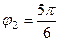. Тогда
= 
= 
= 
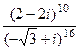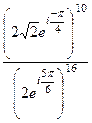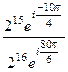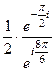здесь в числителе прибавили угол 
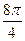, кратный 
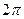, а в знаменателе отняли 
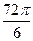. Далее, = 
= 
= 
= 
= 
= 
.
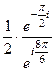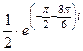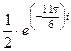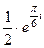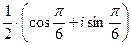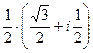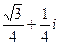Ответ. .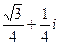
Домашняя задача. Вычислить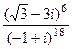 
. Ответ.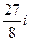 
Задача 31. Вычислить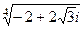 
Решение. Формула: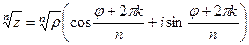 
.
Сначала найдём модуль и аргумент исходного числа.
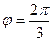(т.к. 90 градусов и ещё 30 во второй четверти),
.
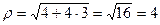Тогда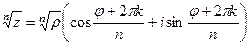 
= 
= 
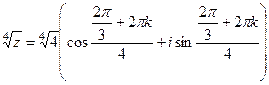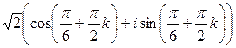таким образом, 4 точки лежат на окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня:
: 
= 
= 
.
: 
= 
= 
.
: 
= 
= 
.
: 
= 
= 
.
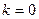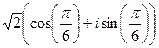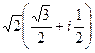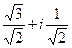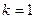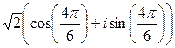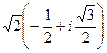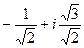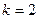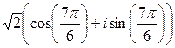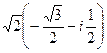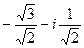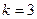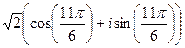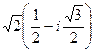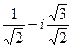Чертёж:
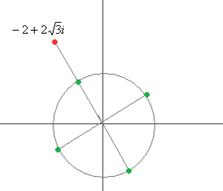
Ответ.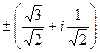 
и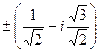 
.
Задача 32. Дано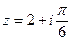 
. Найти 
.
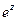Решение.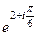 
= 
= 
= 
.
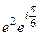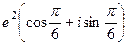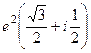Ответ.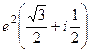 
.
Задача 33. Дано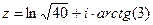 
. Найти .
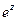Решение.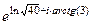 
= 
= 
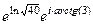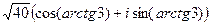. Далее с помощью прямоугольного треугольника вычислим 
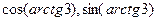. Если надо найти синус и косинус того угла, тангенс которого равен 3, то сначала подпишем длины катетов по известному тангенсу, гипотенуза 
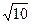вычислится автоматом по теореме Пифагора, а далее будет уже известны синус и косинус.
= 
= 
.
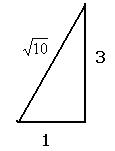
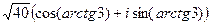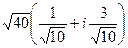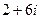Ответ. .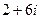
Задача 34. Дано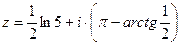 
. Найти .
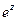Решение.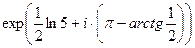 
= 
=
=
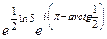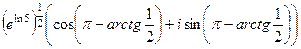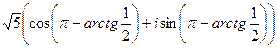. Делаем аналогично тому, как в прошлой задаче, просто треугольник здесь во 2 четверти (угол 
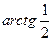отмеряется от 180 в обратном направлении).
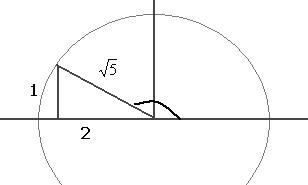
Но гипотенуза всё равно легко вычисляется по теореме Пифагора: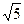 
, тогда 
= 
.
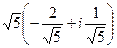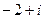Ответ. .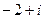
Задача 35. Найти все значения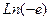 
.
Решение. Используем формулу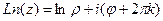 
.
= 
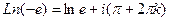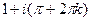. Таким образом, это точки в комплексной плоскости, имеющие вид: 
, 
, 
, ...
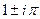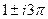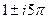Ответ.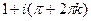 
.
Задача 36. Вычислить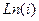 
.
Решение.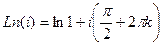 
= 
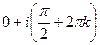. Последовательность значений такова: 
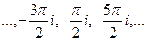каждая соседняя пара отличается на 
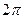по высоте. Здесь сдвиг вверх всего на четверть деления, а не на половину, как для 
.
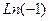Ответ.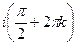 
.
Задача 37. Найти все значения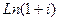 
.
Решение. Используем формулу .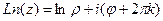
Для числа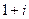 
, 
, 
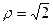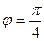. Тогда
.
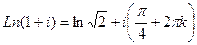Чертёж: бесконечная последовательность точек, на уровне абсциссы
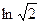, по высоте каждая пара соседних отличается на .
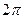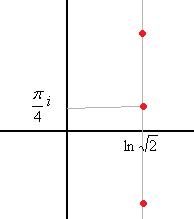
Ответ. .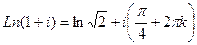
Задача 38. Вычислить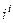 
.
Решение. Представим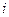 
, расположенную в основании, в виде 
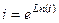. Тогда 
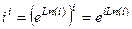, причём чуть выше мы вычисляли
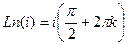. Тогда = 
= 
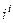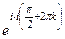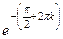т.е. получается бесконечное множество точек на действительной оси.
Ответ.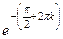 
.
Дата: 2019-11-01, просмотров: 173.
