Многочлены  алгебры логики строятся по аналогии с обычными многочленами. Умножение заменяем конъюнкцией, а сложение альтернативной дизъюнкцией (сложением по модулю два).

Многочленом Жегалкина называется альтернативная дизъюнкция, каждый член которой представляет собой конъюнкцию переменных или переменные, или 1. Любая функция может быть представлена многочленом (полиномом) Жегалкина и это представление единственно. Функция является линейной, если многочлен Жегалкина не содержит конъюнкции переменных.

Образцы решения: Записать булеву функцию 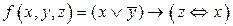 в виде многочлена Жегалкина. Определить является ли функция линейной.

Решение:

Преобразуем равенство, используя формулы алгебры логики.

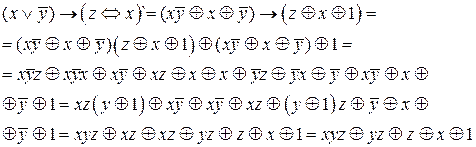
Функция не является линейной, т.к. многочлен Жегалкина содержит конъюнкции переменных.

Ответ: функция не является линейной; многочлен Жегалкина, соответствующий данной функции:

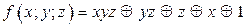
Контрольные вопросы:

1. Определение многочлена Жегалкина.

2. Какой многочлен Жегалкина называется линейным?

Для закрепления теоретического материала и получения прочных знаний решить примеры.

1.Проверить правильность формул, используя таблицы истинности:

= ; ; ;

; .

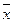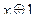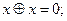
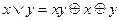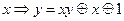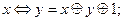
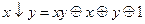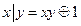2. Выбрать правило исключения альтернативной дизъюнкции :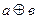

Ответы: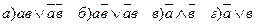

3. Найти среди многочленов Жегалкина линейный:

 Ответы: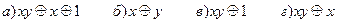

4. 1в.  1. Представить функцию 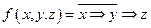 в виде многочлена Жегалкина, используя формулы алгебры логики. Определить, является ли функция линейной.

2. Построить таблицу истинности для функции 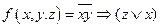, найти СДНФ, упростить ее. Построить контактную схему, реализующую эту функцию. Представить функцию в виде многочлена Жегалкина.

2в 1. Представить функцию 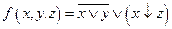 в виде многочлена Жегалкина, используя формулы алгебры логики. Определить, является ли функция линейной. 

2. Построить таблицу истинности для функции 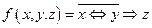, найти СДНФ,  упростить ее. Построить контактную схему, реализующую эту функцию. Представить функцию в виде многочлена Жегалкина.

Представить в виде многочлена Жегалкина 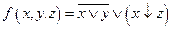, построить контактную схему, реализующую эту функцию.

3в. 1. Представить функцию 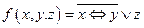 в виде многочлена Жегалкина, используя формулы алгебры логики. Определить, является ли функция линейной. 

2. Построить таблицу истинности для функции 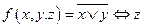, найти СДНФ, упростить ее. Построить контактную схему, реализующую эту функцию. Представить функцию в виде многочлена Жегалкина.

 4в. 1. Представить функцию 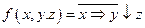 в виде многочлена Жегалкина, используя формулы алгебры логики. Определить, является ли функция линейной. 

2. Построить таблицу истинности для функции 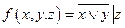, найти СДНФ. Построить контактную схему, реализующую эту функцию. Представить функцию в виде многочлена Жегалкина.

5в. 1. Представить функцию 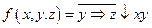 в виде многочлена Жегалкина, используя формулы алгебры логики. Определить, является ли функция линейной. 

2. Построить таблицу истинности для функции 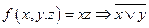, найти СДНФ, упростить ее. Построить контактную схему, реализующую эту функцию. Представить функцию в виде многочлена Жегалкина.

Практическая работа 8