ТОЖДЕСТВЕННО-ИСТИННЫЕ И ТОЖДЕСТВЕННО-ЛОЖНЫЕ ФОРМУЛЫ.
Определение. Формула называется тождественно-истинной (тавто-логией), если для любых наборов переменных она принимает значение И.
Определение. Формула называется тождественно тождественно-ложной, если для любых наборов переменных она принимает значение Л.
В алгебре высказываний используют две нормальные формы: дизъюнктивную и конъюнктивную нормальные формы формулы (ДНФ и КНФ).
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.
Конъюнктивной нормальной формой (КНФ) формулы есть формула, равносильная исходной формуле логики высказываний и записанная в виде конъюнкции элементарных дизъюнкций переменных.
Каждая формула, не равная тождественно Л, может быть приведена СДНФ, которая является единственной с точностью до перестановки дизъюнктивных членов.
Каждая формула, не равная тождественно И, может быть приведена к СКНФ, которая является единственной с точностью до перестановки конъюнктивных членов.
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами
1. Каждое логическое слагаемое формулы содержит все высказывания, входящие в формулу.
2. Все логические слагаемые формулы различны
3. Ни одно логическое слагаемое не содержит высказывание и его отрицание
4. Ни одно логическое слагаемое формулы не содержит одно и то же высказывание дважды.
Алгоритм получения СКНФ по таблице истинности:
1)Отметить те строки , в последнем столбце которых стоят 0:
2)Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке =0, то в дизъюнкцию включают саму эту переменную, если =1, то ее отрицание:
3)Все полученные дизъюнкции связать в конъюнкцию.
1) Образцы решения
Построить таблицу истинности для высказывания: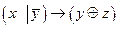 
, построить СНДФ, СКНФ, найти минимальную ДНФ.
Решение.
Строим таблицу истинности- таблицу, с помощью которой устанавливается истинностное значение сложного высказывания при данных значениях входящих в него простых высказываний.
| x | y | z |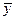 
| 
| 
| |
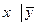
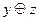
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
По таблице составляем дизъюнктивную нормальную форму (ДНФ). ДНФ в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции нескольких конъюнктов.
Алгоритм получения СДНФ по таблице истинности:
1)Отметить те строки , в последнем столбце которых стоят 1:
2)Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке =1, то в конъюнкцию включают саму эту переменную, если =0, то ее отрицание:
3)Все полученные конъюнкции связать в дизъюнкцию:
Выбираем в таблице строки, в которых булева функция принимает значение 1. В данном случае – это 2-ая, 3-ая, 4-ая, 6-ая и 7-ая строки.
Для каждой строки составляем конъюнкцию: если значение переменной равно 0. то берем ее отрицание, а если 1, то берем саму переменную. Затем составляем дизъюнкцию полученных конъюнкций:
.
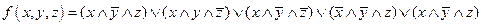Выбираем в таблице строки, в которых булева функция принимает значение 0. В данном случае – это 1-ая, 5-ая, и 8-ая строки:
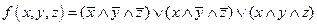
ДНФ называется минимальной, если она содержит наименьшее число букв среди всех ДНФ ей равносильных.
Метод Квайна основывается на применении двух основных соотношений.
Соотношение склеивания :
; 
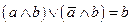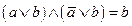
Соотношение поглощения:
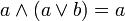
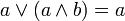
Используя соотношение склеивания получаем:
= 
,
= 
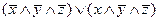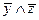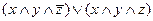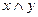. Отсюда,
=( ) 
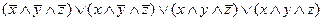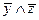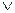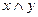( )- сокращенная ДНФ.
Контрольные вопросы:
1) Что такое ДНФ?
2) Чем отличается ДНФ от СДНФ?
3) Как составить ДНФ по таблице истинности?
3) Для закрепления теоретического материала и получения прочных знаний решить примеры.
Построить таблицу истинности, найти СНДФ, найти минимальную ДНФ.
для высказывания:
1в.
1. 
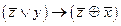
2. 
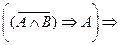
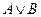
3. 
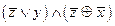
2в.
1. 
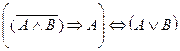
2. 
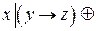
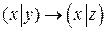
3. 
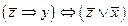
3в
1. 
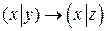
2. 
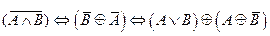
3. 
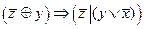
4в.
1. 
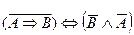
2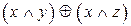 
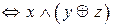
3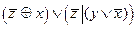 
Построить таблицу истинности, найти СНДФ, найти минимальную ДНФ.
для высказывания:
5в
1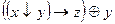 
2. 
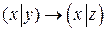
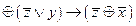
3. 
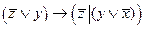
6в
1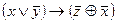 
2. 
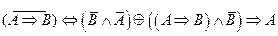
3. 
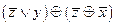
7в.
1. 
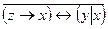
2. 
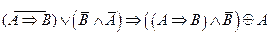
3. 
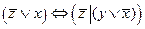
8в.
1. 
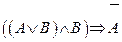
2. 
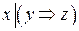
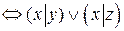
3. 
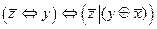
9в
1 .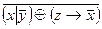 
2. 
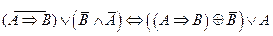
3. 
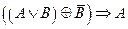
10в.
1. 
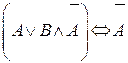
2. 
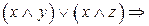
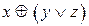
3. 
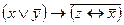
Построить таблицу истинности, найти СНДФ, найти минимальную ДНФ.
для высказывания:
11в.
1 .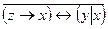
2. 
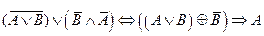
3. 
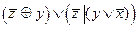
12в.
1. 
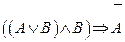
2. 
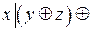
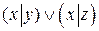
3. 
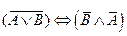
13в.
1.
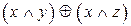
2. 
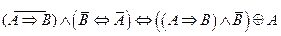
3. 
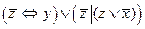
14в
1. 
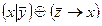
2. 
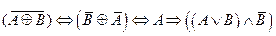
3. 
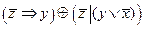
15в
1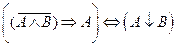 
2. 
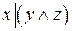
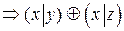
3. 
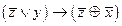
Практическая работа 3
Дата: 2019-11-01, просмотров: 232.
