Преподаватель Сипачева О.И.
Тема: Мощность конечного множества.
Цель работы: уметь решать задачи с помощью кругов Эйлера.
Ход работы.
Повторить краткие теоретические сведения и разобрать задачи с решениями.
2) Повторить краткие теоретические сведения и разобрать задачи с решениями.
Множество А называют подмножеством множества В, если любой элемент множества В является элементом множества В.
Графически это выглядит так
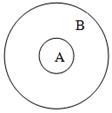
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.
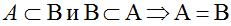
Рассмотрим операции над множествами и их графическую иллюстрацию
1. Объединение множеств А и В изображаем:
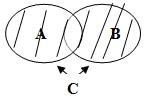
2. Пресечение двух множеств А и В изображаем:
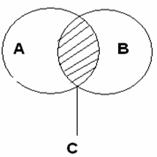В любой имеющей смысл задаче обычно рассматриваются подмножества некоторого "наибольшего" множества U, которое называют универсальным множеством. Универсальное множество - это самое большее множество, содержащее в себе все множества, рассматриваемые в задаче.
Множество всех элементов универсального множества U, не принадлежащих множеству А называется дополнением множества А до U и обозначается Ā
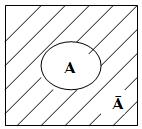
Мощностью конечного множества называется количество его элементов.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
m (A) + m (Ā) = m (E)
А = В => m(A) = m(B)
Для любых конечных множеств справедливы так же утверждения:
M(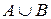 
)=m (A) + m (В) – m (А∩В)
m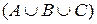 
= m (A) + m (В) + m (С)– m (А∩В) - m (А∩С) – m (В∩С) – m (А∩В∩С).
Решение задач с помощью кругов Эйлера.
Этот способ решать задачи придумал в XVIII в. великий Леонард Эйлер.
Задача.
В олимпиаде по математике приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек. По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек. Ни одной задачи не решили 3 человека. Сколько учащихся решили все задачи? Сколько учащихся решили только две задачи? Сколько учащихся решили только одну задачу?
Решение.
Запишем коротко условие и покажем решение:
m (Е) = 40; m (А) = 20; m (В) = 18; m (С) = 18; m (А∩В) = 7; m (А∩С) = 8; m (В∩С) = 9;
m (АВС) = 3 => m (АВС) = 40 – 3 = 37
Изобразим множества А, В, С (рис.5).
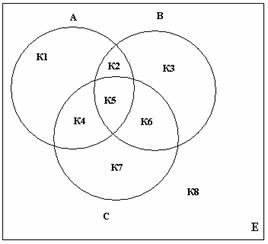
К1 – множество учеников, решивших только одну задачу по алгебре;
К2 – множество учеников, решивших только две задачи по алгебре и геометрии;
К3 – множество учеников, решивших только задачу по геометрии;
К4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;
К5 – множество всех учеников, решивших все три задачи;
К6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;
К7 – множество всех учеников, решивших только задачу по тригонометрии;
К8 – множество всех учеников, не решивших ни одной задачи.
Используя свойство мощности множеств и рисунок можно выполнить вычисления:
m (К5) = m (А∩В∩С)= m (АВС) - m (А) - m (В) - m (С) + m (А∩В) + m (А∩С) + m (В∩С);
m (К5) = 37-20-18-18+7+8+9=5; m (К2) = m (А∩В) - m (К5) = 7-5=2
m (К4) = m (А∩С) - m (К5) = 8-5=3; m (К6) = m (В∩С) - m (К5) = 9-5=4
m (К1) = m (А) - m (К2) - m (К4) - m (К5) = 20-2-3-5=10;
m (К3) = m (В) - m (К2) - m (К6) - m (К5) = 18-2-4-5=7;
m (К7) = m (С) - m (К4) - m (К6) - m (К5) = 18-3-4-5 =6
m (К2) + m (К4) + m (К6) = 2+3+4=9 – число учеников решивших только две задачи;
m (К1) + m (К3) + m (К7) = 10+7+6=23 – число учеников решивших только одну задачу.
Ответ: 5 учеников решили три задачи; 9 учеников решили только по две задачи; 23 ученика решили только по одной задаче.
3) Решить задачи:
Задача № 1. В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского
транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников. Сколько учеников пользуются только одним видом транспорта?
Задача № 2. Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 – в районной.
Сколько шестиклассников:1. Являются читателями обеих библиотек;2. Не являются читателями районной библиотеки;3. Не являются читателями школьной библиотеки; 4. Являются читателями только районной библиотеки;5. Являются читателями только школьной библиотеки?
Задача № 1. Из сотрудников фирмы 16 побывали во Франции,10-в Италии,6-в Англии; в Англии и Италии-5; в Англии и Франции -6; во всех трех странах - 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
Задача №2.В трёх группах 70студентов. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 студентов из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько студентов не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько студентов заняты только спортом?
Задача №5. Часть жителей нашего дома выписывают только газету «Комсомольская правда», часть – только газету «Известия», а часть – и ту, и другую газету. Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%?
Задача №3. Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов. Сколько студентов успешно решили только одну контрольную работу?
Задача №7. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?
Задача №8. В магазине побывало 65 человек. Известно, что они купили 35 холодильников, 36 микроволновок, 37 телевизоров. 20 из них купили и холодильник и микроволновку, 19 - и микроволновку, и телевизор, 15-холодильник и телевизор, а все три покупки совершили три человека. Был ли среди них посетитель, не купивший ничего?
Практическая работа 6
Дата: 2019-11-01, просмотров: 374.
