Преподаватель Сипачева О.И.
Тема: Функции алгебры логики.
Цель работы: знать, уметь
Ход работы.
Повторить краткие теоретические сведения и разобрать задачи с решениями.
Булевы функции
Будем рассматривать логические переменные x1, x2, …, xn , принимающие только два значения: «1» или «0».
Булевой функцией f (x1, x2, …, xn) называется произвольная функция, аргументами которой являются логические переменные и принимающая только одно из двух значений: «1» или «0».
Количество булевых функций одного аргумента равно 22 = 4, это функции:
f1(x) = 0, f2(x) =1, f3 (x) = x и f4(x) =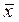 
.
Булевых функций двух аргументов всего 24 = 16, а количество булевых функций n аргументов равно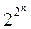 
.
Всякой формуле алгебры логики, составленной из элементарных высказываний x1, x2, …, xn соответствует булева функция f (x1, x2, …, xn), аргументы которой принимают значения истинности соответствующих элементарных высказываний: «1» или «0». Две равносильные формулы алгебры логики определяют одну и ту же булеву функцию, т.к. значения истинности этих формул совпадают для одинаковых значений входящих в них переменных. Для булевых функций можно составлять таблицы значений – всякую булеву функцию n аргументов можно задать таблицей из 2n строк.
Например, таблица значений некоторых функций 2-х аргументов, соответствующих основным логическим операциям (отрицание одного аргумента, конъюнкция, дизъюнкция, импликация и эквиваленция) выглядит так:
| x1 | x2 |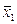 
| x1 Ù x2 | x1 Ú x2 | x1 ® x2 | x1 « x2 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Значение булевой функции f (x1, x2) при известных значениях аргументов устанавливается по строке таблицы, соответствующей заданным значениям x1 и x2. Например, для функции f (x1, x2) = x1 ® x2 значение f (1, 0) = 0, а значение f (1, 1) = 1.
Каждой релейно-контактной схеме (РКС), составленной из переключателей x1, x2, …, xn, можно поставить в соответствие булеву функцию, называемую ее функцией проводимости:
Функция проводимости РКС задается при помощи формулы логики, соответствующей этой РКС. Например, РКС, изображенная на рис. 2,
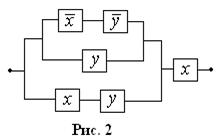
имеет функцию проводимости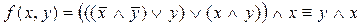 
, таблица значений которой имеет вид:
| х | y | f(x, y) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Любая функция п переменных может быть представлена многочленом (полиномом) Жегалкина и это представление единственно.
Образцы решения:
Записать булеву функцию в виде многочлена Жегалкина. Определить является ли функция линейной.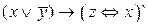 
Решение:
Преобразуем равенство, используя формулы алгебры логики.
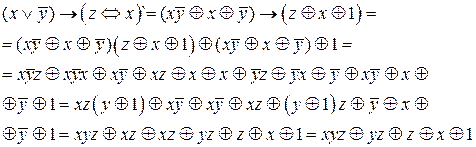
Функция не является линейной, т.к. многочлен Жегалкина содержит конъюнкции переменных.
Ответ: функция не является линейной; многочлен Жегалкина, соответствующий данной функции:
.
.
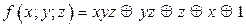
Контрольные вопросы:
1) Для закрепления теоретического материала и получения прочных знаний решить примеры.
18. Построить функцию, двойственную данной: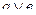 
Ответ: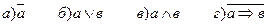 
19. К какому из классов Поста принадлежит функция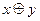 
Ответы: а) Р0 б) Р1 в) S г) ни к какому
18. Построить функцию, двойственную данной: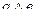 
Ответ: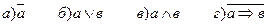
19. К какому из классов Поста принадлежит функция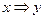 
Ответы: а) Р0 б) Р1 в) S г) ни к какому
18. Построить функцию, двойственную данной: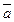 
Ответ: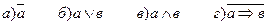 
19. К какому из классов Поста принадлежит функция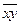 
Ответы: а) Р0 б) Р1 в) S г) ни к какому
18. Построить функцию, двойственную данной: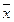 
Ответ: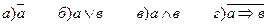 
19. К какому из классов Поста принадлежит функция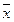 
Ответы: а) Р0 б) Р1 в) S г) ни к какому
Практическая работа 7
Дата: 2019-11-01, просмотров: 282.
