Объединением двух множеств А и В называется множество вида:
AÈB ={a / aÎ A или aÎ B}(рис. 1.2, а).
Пересечением двух множеств А и В называется множество вида:
AÇB={a / aÎ A и aÎ B} (рис. 1.2, б).
Если множества А и В не имеют общих элементов, то AÇB=Æ.
а б
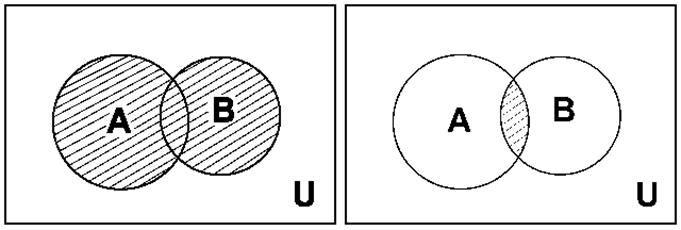
Рис. 1.2.
Свойства операций объединения и пересечения
1. AÈB = ВÈА, AÇB = ВÇА (коммутативность);
2. (AÈB)ÈС = AÈ(BÈС), (AÇB)ÇС = AÇ(BÇС) (ассоциативность).
Объединение и пересечение связаны законами дистрибутивности:
AÇ(BÈC)= (AÇB) È (AÇС); AÈ(BÇC)= (AÈB) Ç (AÈС).
По свойству 3 операции включения следует равенство правой и левой частей доказываемого равенства.
Для операции объединения множеств нейтральным является пустое множество Æ, а для операции пересечения множеств - универсальное множество U.
Разность множеств А и В определяется следующим образом:
A\B ={a / aÎA и aÏB} (рис. 1.3, а).
Разность не обладает свойством коммутативности; эта операция также не является и ассоциативной.
Пользуясь понятием универсального множества, можно определить дополнение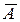 
к множеству А, как разность вида: 
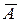= U \ A (рис. 1.3, б).
Пример. Пусть в качестве универсального множества выступает множество целых чисел Z и пусть А - это множество всех чётных чисел. Тогда 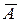- это множество всех нечётных чисел.
Операции объединения, пересечения и дополнения множеств связаны между собой законами де Моргана:
, 
.
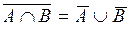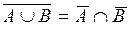Если a Î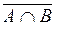 
, то a Ï AÇB. Это значит, что или aÎ 
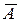, или aÎ 
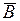, т.е. aÎ 
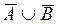. Следовательно, 
.
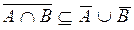С другой стороны, если aÎ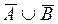 
, то или aÎ 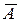, или aÎ 
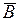. Это значит, что aÏ AÇ B , т.е. a Î 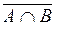. Таким образом, 
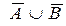Í .
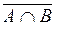Из этих двух включений следует первый закон де Моргана. ÿ
Второй закон доказывается аналогичным образом.
а б
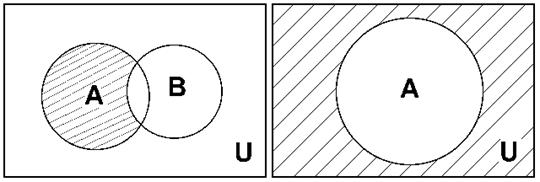
Рис. 1.3.
Образцы решения задач.
1. Найти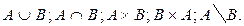 
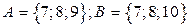
Решение: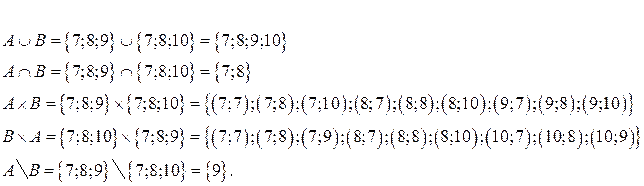 
2. Доказать равенство и записать двойственное ему:
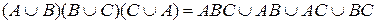
Решение:
Преобразуем левую часть:
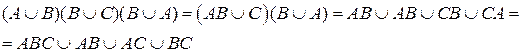
Таким образом, левая часть равна правой части, т.е. равенство верно.
Для того чтобы составить равенство, двойственное данному, пользуемся принципом двойственности. Заменим в данном равенстве знак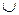 
на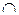 
и наоборот. Чтобы не поменялся порядок действий, по другому поставим скобки. Получим двойственное равенство: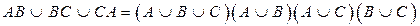 
Контрольные вопросы:
1. Что понимают под множеством?
2. Способы задания множеств.
3. Какое множество называют пустым? Универсальным?
4. Действия над множествами.
5. Законы действий над множествами.
Задание 1.
1 вариант.
1. Найти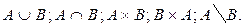 
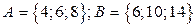
2. Доказать равенство и записать двойственное ему:
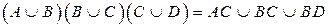
3.Даны множества M, P, T. Каким будет множество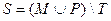 
, если
.
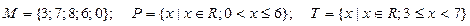Найдите его. Изобразите его с помощью кругов Эйлера.
2 вариант.
1. Найти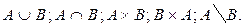 
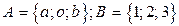
2. Доказать равенство и записать двойственное ему:
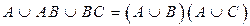
3. Даны множества M, P, T. Каким будет множество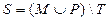 
, если
.
Найдите его. Изобразите его с помощью кругов Эйлера.
3 вариант.
1. Найти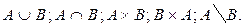 
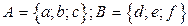
2. Доказать равенство и записать двойственное ему:
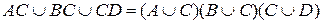
3. Даны множества M, P, T. Каким будет множество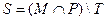 
, если
4 вариант.
1. Найти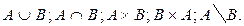 
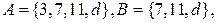
2. Доказать равенство и записать двойственное ему:
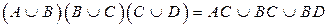
3.Даны множества M, P, T. Каким будет множество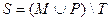 
, если
.
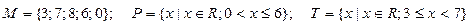Найдите его. Изобразите его с помощью кругов Эйлера.
5 вариант. 1. Найти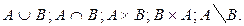 
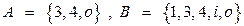
2. Доказать равенство и записать двойственное ему:
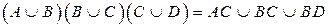
3.Даны множества M, P, T. Каким будет множество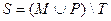 
, если
.
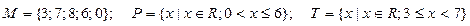Найдите его. Изобразите его с помощью кругов Эйлера.
6 вариант.
1. Найти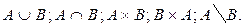 
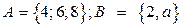
2. Доказать равенство и записать двойственное ему:
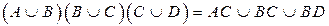
3.Даны множества M, P, T. Каким будет множество 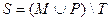, если
.
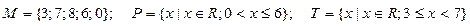Найдите его. Изобразите его с помощью кругов Эйлера.
7 вариант.
1. Найти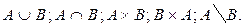 
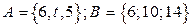
2. Доказать равенство и записать двойственное ему:
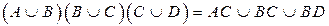
3.Даны множества M, P, T. Каким будет множество 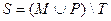, если
.
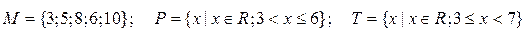Найдите его. Изобразите его с помощью кругов Эйлера.
8 вариант.
1. Найти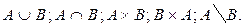 
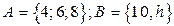
2. Доказать равенство и записать двойственное ему:
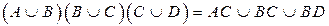
3.Даны множества M, P, T. Каким будет множество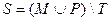 
, если
.
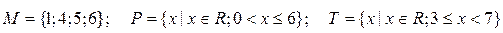Найдите его. Изобразите его с помощью кругов Эйлера.
9 вариант.
1. Найти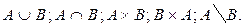 
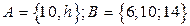
2. Доказать равенство и записать двойственное ему:
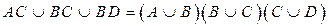
3.Даны множества M, P, T. Каким будет множество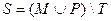 
, если
.
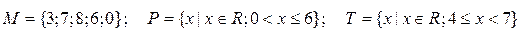Найдите его. Изобразите его с помощью кругов Эйлера.
10 вариант.
1. Найти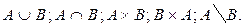 
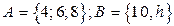
2. Доказать равенство и записать двойственное ему:
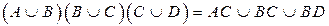
3.Даны множества M, P, T. Каким будет множество 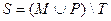, если
.
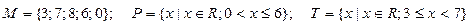Найдите его. Изобразите его с помощью кругов Эйлера.
Задание 2. Заданы множества А, В, С. Какие из утверждений будут верными?
a) Множества A и C не содержат одинаковых элементов.
b) Множества A и C равны ( A = C ).
c) Множества В и C равны ( B = C ).
d) Множество А является подмножеством множества В. ( A Ì B )
e) Множество С является подмножеством множества А. (C Ì A )
f) Множество С является подмножеством множества B. (C Ì B )
g) Пустое множество Æ является подмножеством множества А.
i) Множество А конечно.
j) Множество В является бесконечным.
k) Множество В является подмножеством пустого множества/
Вариант 0. A = {1,2,a,b} , B = {2,a} , C = {a,1,2,b} .
Вариант 1. A = {2,3,4, f } , B = {3,4} , C = {4,3} .
Вариант 2. A = {7,9,a} , B = {a,9,7} , C = {7,8,9,a,b} .
Вариант 3. A = {5,6,t} , B = {4,5,6,e,t} , C = {6,t,5} .
Вариант 4. A = {3,4,o} , B = {1,3,4,i,o} , C = {o,1,3,i,4} .
Вариант 5. A = {9,10,h,l} , B = {h,l,9,10} , C = {10,h} .
Вариант 6. A = {3,6,9,u} , B = {6,u,9} , C = {6,u,3,9} .
Вариант 7. A = {6,8,10} , B = {4,6,8,10, k} , C = {8,6, k,4,10} .
Вариант 8. A = {- 5,5,t} , B = {5,- 5,t} , C = {- 5, k,t,5} .
Вариант 9. A = {- 1,t, r} , B = {- 2,- 1,0,t, r} , C = {t,- 1, r} .
Вариант 10. A = {3,7,11,d} , B = {7,11,d} , C = {11,d,7} .
Задание 3.Расположите множества: A È B , A \ B , AÈ B È C , A/(B Ç C) , в таком порядке,
чтобы каждое из них являлось подмножеством предыдущего множества.
Вариант 1. Заданы произвольные множества А, В, С.
Расположите множества: AÈ B È C , A \ B , A È B , A , в таком порядке, чтобы
каждое из них было подмножеством следующего за ним.
Вариант 2. Заданы произвольные множества А, В, С.
Расположите множества: B È C , C \ A ,C \ (A È B) , A È B È C , в таком порядке,
чтобы каждое из них включало в себя предыдущее множество.
Вариант 3. Заданы произвольные множества А, В, С.
Расположите множества: C , B È C , A Ç B Ç C , A Ç C в таком порядке, чтобы
каждое из них включало в себя множество, следующее за ним.
Вариант 4. Заданы произвольные множества А, В, С.
Расположите множества: A È B , AÇ B Ç C , A È B È C , A È (B Ç C) , в таком
порядке, чтобы каждое из них было подмножеством предыдущего
множества.
Вариант 5. Заданы произвольные множества А, В, С.
Расположите множества: A Ç B , A È B È C , A Ç B Ç C , A Ç (B È C) , в таком
порядке, чтобы каждое из них являлось подмножеством следующего за
ним.
Вариант 6. Заданы произвольные множества А, В, С.
Расположите множества: AÇ B , AÈ B , A È B È C , A , в таком порядке, чтобы
каждое из них содержало предыдущее множество.
Вариант 7. Заданы произвольные множества А, В, С.
Расположите множества: B È C , B \ (A È C) , B , AÈ B È C , в таком порядке,
чтобы каждое из них содержало множество, следующее за ним.
Вариант 8. Заданы произвольные множества А, В, С.
Расположите множества: B È C , AÇ B Ç C , B Ç C ,C È (B \ A) , в таком
порядке, чтобы каждое из них являлось подмножеством предыдущего
множества.
Вариант 9. Заданы произвольные множества А, В, С.
Расположите множества: AÈ B , A Ç B Ç C , A È B È C , A Ç B , в таком порядке,
чтобы каждое из них было подмножеством следующего за ним.
Вариант 10. Заданы произвольные множества А, В, С.
Расположите множества: AÈ B , B , A È B È C , B È (A \ C) , в таком порядке,
чтобы каждое из них включало в себя предыдущее множество._
Задание 4. Заданы множества А, В.
Найдите: AÈ B , A Ç B , A \ B , B \ A, AÈ Æ , B Ç Æ , A \ Æ ,Æ \ B .
Вариант 0. A = {1,2,4,5, k,l} , B = {2,3,4,5,l,m} .
Вариант 1. A = {3,t,o,4,5} , B = {2,3,5,o, p} .
Вариант 2. A = {5,6,8, y,u, r} , B = {6,7,8, y,m, r} .
Вариант 3. A = {- 1,2,3, f ,h} , B = {0,1,2,3, f ,l} .
Вариант 4. A = {- 3,- 2,0,1, j, k} , B = {- 1,0,1,2, k, p} .
Вариант 5. A = {4,6,8,10,m,n} , B = {1,4,7,10,m, r} .
Вариант 6. A = {2,3,6,7,i, y} , B = {3,4,5,6,i, y, x} .
Вариант 7. A = {a,b,c,3,6,9} , B = {b,c,d,6,7,8} .
Вариант 8. A = {x, y, z,2,3,4} , B = {3,4,5, s,t, y} .
Вариант 9. A = {a,2,d,3, k,5} , B = {1,d,2,a,4,m} .
Вариант 10. A = {- 5,- 2,2,w,o} , B = {- 8,- 5,- 2,0,o, p} .
Задание 5. Принято обозначать:
N – множество натуральных чисел; Q – множество рациональных чисел;
Z – множество целых чисел; R – множество действительных чисел.
Тогда верным утверждением будут…
Вариант 0. a) 2.1Î N , b) 2.7 Î Q , c) - 5Î Z , d) 7 Î R .
Вариант 1. a) 6Î N , b) - 2.3Î Q, c) 3 Î Z , d) p Î R .
Вариант 2. a) - 2Î N , b) 5 Î Q, c) 7 Î Z , d) 8 Î R .
Вариант 3. a)1.9Î N , b) 5,6Î Q, c) 0.7 Î Z , d) - 3 Î R .
Вариант 4. a) 7 Î N , b) -2 Î Q, c) - 3 Î Z , d) - 4Î R .
Вариант 5. a) - 3Î N , b) 11Î Q , c) - 15Î Z , d) - 7 Î R .
Вариант 6.а) 4,3Î N ; b)3.14Î Q , c) 15Î Z , d) - 9 Î R .
Вариант 7. a) 7 Î N , b) - 5.17Î Q, c) 2.5Î Z , d) 3Î R .
Вариант 8. a)8Î N , b) - 16 Î Q, c) - 2Î Z , d) - 11Î R .
Вариант 9. a) 7.2Î N , b) 13 Î Q, c) 6,5Î Z , d) - 25 Î R .
Вариант 10. a) 9 Î N , b)12.
Практическая работа 5
Дата: 2019-11-01, просмотров: 741.
