Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

(по книге: Сидоренко Е. В. Методы математической обработки в психологии. — СПб., 2004 — С.316-321)

 

Различия между двумя выборками можно считать значимыми (р<0,05), если U_эмп ≤ _{табл., 0,05} и тем более достоверными (р<0,01), если U_эмп ≤ U_{табл., 0,01}

Таблица 49

N 1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18 | 19		20
N 2	р=0,05
3	-	0
4	-	0	1
5	0	1	2	4
6	0	2	3	5	7
7	0	2	4	6	8	11
8	1	3	5	8	10	13	15
9	1	4	6	9	12	15	18	21
10	1	4	7	И	14	17	20	24	27
11	1	5	8	12	16	19	23	27	31	34
12	2	5	9	13	17	21	26	30	34	38	42
13	2	6	10	15	19	24	28	33	37	42	47	51
14	3	7	11	16	21	26	31	36	41	46	51	56	61
15	3	7	12	18	23	28	33	39	44	50	55	61	66	72
16	3	8	14	19	25	30	36	42	48	54	60	65	71	77	83
17	3	9	15	20	26	33	39	45	51	57	64	70	77	83	89	96
18	4	9	16	22	28	35	41	48	55	61	68	75	82	88	95	102	109
19	4	10	17	23	30	37	44	51	58	65	72	80	87	94	101	109	116	123
20	4	11	18	25	32	39	47	54	62	69	77	84	92	100	107	115	123	130	138
р=0,01
5	-	-	0	1
6	-	-	1	2	3
7	-	0	1	3	4	6
8	-	0	2	4	6	7	9
9	-	1	3	5	7	9	11	14
10	-	1	3	6	8	И	13	16	19
11	-	1	4	7	9	12	15	18	22	25
12	-	2	5	8	11	14	17	21	24	28	31
13	0	2	5	9	12	16	20	23	27	31	35	39
14	0	2	6	10	13	17	22	26	30	34	38	43	47
15	0	3	7	11	15	19	24	28	33	37	42	47	51	56
16	0	3	7	12	16	21	26	31	36	41	46	51	56	61	66
17	0	4	8	13	18	23	28	33	38	44	49	55	60	66	71	77
18	0	4	9	14	19	24	30	36	41	47	53	59	65	70	76	82	88
19	1	4	9	15	20	26	32	38	44	50	56	63	69	75	82	88	94	101
20	1	5	10	16	22	28	34	40	47	53	60	67	73	80	87	93	100	107	114

 

Продолжение таблицы 49

N 1	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
N 2	р=0,05
21	19	26	34	41	49	57	65	73	81	89	97	105	113	121	130	138	146	154
22	20	28	36	44	52	60	69	77	85	94	102	111	119	128	136	145	154	162
23	21	29	37	46	55	63	72	81	90	99	107	116	125	134	143	152	161	170
24	22	31	39	48	57	66	75	85	94	103	ИЗ	122	131	141	150	160	169	179
25	23	32	41	50	60	69	79	89	98	108	118	128	137	147	157	167	177	187
26	24	33	43	53	62	72	82	93	103	113	123	133	143	154	164	174	185	195
27	25	35	45	55	65	75	86	96	107	118	128	139	150	160	171	182	193	203
28	26	36	47	57	68	79	89	100	111	122	133	144	156	167	178	189	200	212
29	27	38	48	59	70	82	93	104	116	127	139	150	162	173	185	196	208	220
30	28	39	50	62	73	85	96	108	120	132	144	156	168	180	192	204	216	228
31	29	41	52	64	76	88	100	112	124	137	149	161	174	186	199	211	224	236
32	30	42	54	66	78	91	103	116	129	141	154	167	180	193	206	219	232	245
33	31	43	56	68	81	94	107	120	133	146	159	173	186	199	213	226	239	253
34	32	45	58	71	84	97	110	124	137	151	164	178	192	206	219	233	247	261
35	33	46	59	73	86	100	114	128	142	156	170	184	198	212	226	241	255	269
36	35	48	61	75	89	103	117	132	146	160	175	189	204	219	233	248	263	278
37	36	49	63	77	92	106	121	135	150	165	180	195	210	225	240	255	271	286
38	37	51	65	79	94	109	124	139	155	170	185	201	216	232	247	263	278	294
39	38	52	67	82	97	112	128	143	159	175	190	206	222	238	254	270	286	302
40	39	53	69	84	100	115	131	147	163	179	196	212	228	245	261	278	294	311
р=0,01
21	10	16	22	29	35	42	49	56	63	70	77	84	91	98	105	113	120	127
22	10	17	23	30	37	45	52	59	66	74	81	89	96	104	111	119	127	134
23	И	18	25	32	39	47	55	62	70	78	86	94	102	109	117	125	133	141
24	12	19	26	34	42	49	57	66	74	82	90	98	107	115	123	132	140	149
25	12	20	27	35	44	52	60	69	77	86	95	103	112	121	130	138	147	156
26	13	21	29	37	46	54	63	72	81	90	99	108	117	126	136	145	154	163
27	14	22	30	39	48	57	66	75	85	94	103	113	122	132	142	151	161	171
28	14	23	32	41	50	59	69	78	88	98	108	118	128	138	148	158	168	178
29	15	24	33	42	52	62	72	82	92	102	112	123	133	143	154	164	175	185
30	15	25	34	44	54	64	75	85	95	106	117	127	138	149	160	171	182	192
31	16	26	36	46	56	67	77	88	99	110	121	132	143	155	166	177	188	200
32	17	27	37	47	58	69	80	91	103	114	126	137	149	160	172	184	195	207
33	17	28	38	49	60	72	83	95	106	118	130	142	154	166	178	190	202	214
34	18	29	40	51	62	74	86	98	110	122	134	147	159	172	184	197	209	222
35	19	30	41	53	64	77	89	101	114	126	139	152	164	177	190	203	216	229
36	19	31	42	54	67	79	92	104	117	130	143	156	170	183	196	210	223	236
37	20	32	44	56	69	81	95	108	121	134	148	161	175	189	202	216	230	244
38	21	33	45	58	71	84	97	111	125	138	152	166	180	194	208	223	237	251
39	21	34	46	59	73	86	100	114	128	142	157	171	185	200	214	229	244	258
40	22	35	48	61	75	89	103	117	132	146	161	176	191	206	221	236	251	266

 

Продолжение таблицы 49

N 1	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
N 2	р=0,05
41	40	55	70	86	102	118	135	151	168	184	201	218	234	251	268	285	302	319
42	41	56	72	88	105	121	138	155	172	189	206	223	240	258	275	292	310	327
43	42	58	74	91	107	124	142	159	176	194	211	229	247	264	282	300	318	335
44	43	59	76	93	110	128	145	163	181	199	216	235	253	271	289	307	325	344
45	44	61	78	95	ИЗ	131	149	167	185	203	222	240	259	277	296	315	333	352
46	45	62	80	97	115	134	152	171	189	208	227	246	265	284	303	322	341	360
47	46	64	81	100	118	137	156	175	194	213	232	251	271	290	310	329	349	369
48	47	65	83	102	121	140	159	178	198	218	237	257	277	297	317	337	357	377
49	48	66	85	104	123	143	163	182	202	222	243	263	283	303	324	344	365	385
50	49	68	87	106	126	146	166	186	207	227	248	268	289	310	331	352	372	393
51	50	69	89	109	129	149	170	190	211	232	253	274	295	316	338	359	380	402
52	51	71	91	111	131	152	173	194	215	237	258	280	301	323	345	366	388	410
53	52	72	92	113	134	155	177	198	220	241	263	285	307	329	352	374	396	418
54	53	74	94	115	137	158	180	202	224	246	269	291	313	336	359	381	404	427
55	54	75	96	118	139	161	184	206	228	251	274	297	319	342	365	389	412	435
56	55	76	98	120	142	164	187	210	233	256	279	302	326	349	372	396	420	443
57	57	78	100	122	145	167	191	214	237	261	284	308	332	355	379	403	427	451
58	58	79	102	124	147	171	194	218	241	265	289	314	338	362	386	411	435	460
59	59	81	103	127	150	174	198	222	246	270	295	319	344	369	393	418	443	468
60	60	82	105	129	153	177	201	225	250	275	300	325	350	375	400	426	451	476
р=0,01
41	23	36	49	63	77	91	106	121	136	151	166	181	196	211	227	242	258	273
42	23	37	50	65	79	94	109	124	139	155	170	186	201	217	233	249	265	280
43	24	38	52	66	81	96	112	127	143	159	175	190	207	223	239	255	271	288
44	25	39	53	68	83	99	115	130	146	163	179	195	212	228	245	262	278	295
45	25	40	54	70	85	101	117	134	150	167	183	200	217	234	251	268	285	303
46	26	41	56	71	87	104	120	137	154	171	188	205	222	240	257	275	292	310
47	27	42	57	73	90	106	123	140	157	175	192	210	228	245	263	281	299	317
48	27	43	58	75	92	109	126	143	161	179	197	215	233	251	269	288	306	325
49	28	44	60	77	94	111	129	147	165	183	201	220	238	257	276	294	313	332
50	29	45	61	78	96	114	132	150	168	187	206	225	244	263	282	301	320	339
51	29	46	63	80	98	116	135	153	172	191	210	229	249	268	288	307	327	347
52	30	47	64	82	100	119	137	157	176	195	215	234	254	274	294	314	334	354
53	31	48	65	83	102	121	140	160	179	199	219	239	259	280	300	320	341	361
54	31	49	67	85	104	114	143	163	183	203	224	244	265	285	306	327	348	369
55	32	50	68	87	106	126	146	166	187	207	228	249	270	291	312	333	355	376
56	33	51	69	89	108	129	149	177	190	211	233	254	275	297	318	340	362	384
57	33	52	71	90	111	131	152	173	194	215	237	259	281	302	324	347	369	391
58	34	53	72	92	113	133	155	176	198	220	242	264	286	308	331	353	376	398
59	34	54	73	94	115	136	158	179	201	224	246	268	291	314	337	360	383	406
60	35	55	75	96	117	138	160	183	205	228	250	273	296	320	343	366	390	413

 

Продолжение таблицы 49

N 1	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
N 2	р=0,05
21
22	171
23	180	189
24	188	198	207
25	197	207	217	227
26	206	216	226	237	247
27	214	225	236	247	258	268
28	223	234	245	257	268	279	291
29	232	243	255	267	278	290	302	314
30	240	252	265	277	289	301	313	326	338
31	249	261	274	287	299	312	325	337	350	363
32	258	271	284	297	310	323	336	349	362	375	389
33	266	280	293	307	320	334	347	361	374	388	402	415
34	275	289	303	317	331	345	359	373	387	401	415	429	443
35	284	298	312	327	341	356	370	385	399	413	428	442	457	471
36	292	307	322	337	352	367	381	396	411	426	441	456	471	486	501
37	301	316	332	347	362	378	393	408	424	439	454	470	485	501	516	531
38	310	325	341	357	373	388	404	420	436	452	467	483	499	515	531	547	563
39	318	335	351	367	383	399	416	432	448	464	481	497	513	530	546	562	579	595
40	327	344	360	377	394	410	427	444	460	477	494	511	527	544	561	578	594	611	628
р=0,01
21
22	142
23	150	158
24	154	166	174
25	165	174	183	192
26	173	182	191	201	210
27	180	190	200	209	219	229
28	188	198	208	218	229	239	249
29	196	206	217	227	238	249	259	270
30	203	214	225	236	247	258	270	281	292
31	211	223	234	245	257	268	280	291	303	314
32	219	231	242	254	266	278	290	302	314	326	338
33	227	239	251	263	276	288	300	313	325	337	350	362
34	234	247	260	272	285	298	311	323	336	349	362	375	387
35	242	255	268	281	294	308	321	334	347	360	374	387	400	413
36	250	263	277	290	304	318	331	345	358	372	386	399	413	427	440
37	258	271	285	299	313	327	341	355	370	384	398	412	426	440	454	468
38	265	280	294	308	323	337	352	366	381	395	410	424	439	453	468	482	497
39	273	288	303	317	332	347	362	377	392	407	422	437	452	467	482	497	512	527
40	281	296	311	326	342	357	372	388	403	418	434	449	465	480-	495	511	526	542	557

 

Продолжение таблицы 49

N 1	41	42	43	44	45	46	47	48	49	50
N 2	р=0,05
41	662
42	679	697
43	697	715	733
44	714	733	751	770
45	731	750	769	789	808
46	749	768	788	807	827	846
47	766	786	806	826	846	866	886
48	783	804	824	845	865	886	906	927
49	800	821	842	863	884	905	926	947	968
50	818	839	861	882	903	925	946	968	989	1010
51	835	857	879	901	922	944	966	988	1010	1032
52	852	875	897	919	942	964	986	1009	1031	1053
53	870	893	915	938	961	934	1006	1029	1052	1075
54	887	910	934	957	980	1003	1026	1050	1073	1096
55	904	928	952	975	999	1023	1046	1070	1094	1113
56	922	946	970	994	1018	1042	1067	1091	1115	1139
57	939	964	981	1013	1037	1062	1087	1111	1136	1161
58	956	981	1007	1032	1057	1082	1107	1132	1157	1182
59	974	999	1025	1050	1076	1101	1127	1152	1178	1204
60	991	1017	1043	1069	1095	1121	1147	1173	1199	1225
р=0,01
41	589
42	605	621
43	621	637	654
44	636	654	671	688
45	652	670	688	706	723
46	668	687	705	723	741	759
47	684	703	722	740	759	777	796
48	700	719	738	757	776	795	814	834
49	716	736	755	775	794	814	833	853	872
50	732	752	772	792	812	832	852	872	892	912
51	748	769	789	809	830	850	870	891	911	932
52	764	785	806	827	847	868	889	910	931	951
53	780	802	823	844	865	886	908	929	950	971
54	796	818	840	861	883	905	926	948	970	991
55	812	834	857	879	901	923	945	967	989	1011
56	828	851	873	896	919	941	964	986	1009	1031
57	844	867	890	913	936	959	982	1005	1028	1051
58	861	884	907	931	954	978	1001	1024	1048	1071
59	877	900	924	948	972	996	1020	1044	1068	1091
60	893	917	941	965	990	1014	1038	1063	1087	1111

 

Окончание таблицы 49

N 1	51	52	53	54	55	56	57	58	59	60
N 2	р=0,05
41
42
43
44
45
46
47
48
49
50
51	1054
52	1076	1098
53	1098	1120	1143
54	1119	1143	1166	1189
55	1141	1165	1189	1213	1236
56	1163	1187	1212	1236	1260С	1284
57	1185	1210	1235	1259	1284	1309	1333
58	1207	1232	1257	1283	1308	1333	1358	1383
59	1229	1255	1280	1306	1331	1357	1383	1408	1434
60	1251	1277	1303	1329	1355	1381	1407	1433	1460С	1486
р=0,01
41
42
43
44
45
46
47
48
49
50
51	952
52	972	993
53	993	1014	1035
54	1013	1035	1057	1078
55	1034	1056	1078	1100	1122
56	1054	1077	1099	1122	1145	1167
57	1074	1098	1121	1141	1167	1190	1213
58	1095	1118	1142	1165	1189	1213	1236	1260
59	1115	1139	1163	1187	1211	1235	1259	1283	1307
60	1136	1160	1185	1209	1234	1258	1282	1307	1331	1356

 

 1.8. Критические значения непараметрического критерия Вилкоксона

(по книге: Сидоренко Е. В. Методы математической обработки в психологии. – СПб., 1996. – С. 324)

При Т _расч. £ Т _{табл., a , N} различия статистически значимы.

Таблица 50

N	a =0,05	a =0,01	N	a =0,05	a =0,01
5	0	—	28	130	101
6	2	—	29	140	110
7	3	0	30	151	120
8	5	1	31	163	130
9	8	3	32	175	140
10	10	5	33	187	151
11	13	7	34	200	162
12	17	9	35	213	173
13	21	12	36	227	185
14	25	15	37	241	198
15	30	19	38	256	211
16	35	23	39	271	224
17	41	27	40	286	238
18	47	32	41	302	252
19	53	37	42	319	266
20	60	43	43	336	281
21	67	49	44	353	296
22	75	55	45	371	312
23	83	62	46	389	328
24	91	69	47	407	345
25	100	76	48	426	362
26	110	84	49	446	379
27	119	92	50	466	397

 

 

1.9. Таблицы для перевода процентных долей в величины центрального угла для расчета критерия «угловое преобразование» Фишера

(из книги: Ермолаев О. Ю. Математическая статистика для психологов. — М., 2002 — С.308-312)

Величины угла φ (в радианах) для разных процентных долей: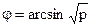

Таблица 51

% доля	%, сотый знак
	0		1		2		3		4		5		6		7	8	9
	Значения
0,0	0,000	0,020		0,028		0,035		0,040		0,045		0,049		0,053		0,057	0,060
0,1	0,063	0,066		0,069		0,072		0,075		0,077		0,080		0,082		0,085	0,087
0,2	0,089	0,092		0,094		0,096		0,098		0,100		0,102		0,104		0,106	0,108
0,3	0,110	0,111		0,113		0,115		0,117		0,118		0,120		0,122		0,123	0,125
0,4	0,127	0,128		0,130		0,131		0,133		0,134		0,136		0,137		0,139	0,140
0,5	0,142	0,143		0,144		0,146		0,147		0,148		0,150		0,151		0,153	0,154
0,6	0,155	0,156		0,158		0,159		0,160		0,161		0,163		0,164		0,165	0,166
0,7	0,168	0,169		0,170		0,171		0,172		0,173		0,175		0,176		0,177	0,178
0,8	0,179	0,180		0,182		0,183		0,184		0,185		0,186		0,187		0,188	0,189
0,9	0,190	0,191		0,192		0,193		0,194		0,195		0,196		0,197		0,198	0,199

 

Продолжение таблицы 51

% доля	%, последний десятичный знак
	0		1		2		3		4		5		6		7	8	9
	Значения
1	0,200	0,210		0,220		0,229		0,237		0,246		0,254		0,262		0,269	0,277
2	0,284	0,291		0,298		0,304		0,311		0,318		0,324		0,330		0,336	0,342
3	0,348	0,354		0,360		0,365		0,371		0,376		0,382		0,387		0,392	0,398
4	0,403	0,408		0,413		0,418		0,423		0,428		0,432		0,437		0,442	0,446
5	0,451	0,456		0,460		0,465		0,469		0,473		0,478		0,482		0,486	0,491
6	0,495	0,499		0,503		0,507		0,512		0,516		0,520		0,524		0,528	0,532
7	0,536	0,539		0,543		0,547		0,551		0,555		0,559		0,562		0,566	0,570
8	0,574	0,577		0,581		0,584		0,588		0,592		0,595		0,599		0,602	0,606
9	0,609	0,613		0,616		0,620		0,623		0,627		0,630		0,633		0,637	0,640
10	0,644	0,647		0,650		0,653		0,657		0,660		0,663		0,666		0,670	0,673
11	0,676	0,679		0,682		0,686		0,689		0,692		0,695		0,698		0,701	0,704
12	0,707	0,711		0,714		0,717		0,720		0,723		0,726		0,729		0,732	0,735
13	0,738	0,741		0,744		0,747		0,750		0,752		0,755		0,758		0,761	0,764 /
14	0,767	0,770		0,773		0,776		0,778		0,781		0,784		0,787		0,790	0,793
15	0,795	0,798		0,801		0,804		0,807		0,809		0,812		0,815		0,818	0,820

Продолжение таблицы 51

% доля	%, последний десятичный знак
	0		1		2		3		4		5		6		7	8	9
	Значения
16	0,823	0,826		0,828		0,831		0,834		0,837		0,839		0,842		0,845	0,847
17	0,850	0,853		0,855		0,858		0,861		0,863		0,866		0,868		0,871	0,874
18	0,876	0,879		0,881		0,884		0,887		0,889		0,892		0,894		0,897	0,900
19	0,902	0,905		0,907		0,910		0,912		0,915		0,917		0,920		0,922	0,925
20	0,927	0,930		0,932		0,935		0,937		0,940		0,942		0,945		0,947	0,950
21	0,952	0,955		0,957		0,959		0,962		0,964		0,967		0,969		0,972	0,974
22	0,976	0,979		0,981		0,984		0,986		0,988		0,991		0,993		0,996	0,998
23	1,000	1,003		1,005		1,007		1,010		1,012		1,015		1,017		1,019	1,022
24	1,024	1,026		1,029		1,031		1,033		1,036		1,038		1,040		1,043	1,045
25	1,047	1,050		1,052		1,054		1,056		1,059		1,061		1,063		1,066	1,068
26	1,070	1,072		1,075		1,077		1,079		1,082		1,084		1,086		1,088	1,091
27	1,093	1,095		1,097		1,100		1,102		1,104		1,106		1,109		1,111	1,113
28	1,115	1,117		1,120		1,122		1,124		1,126		1,129		1,131		1,133	1,135
29	1,137	1,140		1,142		1,144		1,146		1,148		1,151		1,153		1,155	1,157
30	1,159	1,161		1,164		1,166		1,168		1,170		1,172		1,174		1,177	1,179
31	1,182	1,183		1,185		1,187		1,190		1,192		1,194		1,196		1,198	1,200
32	1,203	1,205		1,207		1,209		1,211		1,213		1,215		1,217		1,220	1,222
33	1,224	1,226		1,228		1,230		1,232		1,234		1,237		1,239		1,241	1,243
34	1,245	1,247		1,249		1,251		1,254		1,256		1,258		1,260		1,262	1,264
35	1,266	1,268		1,270		1,272		1,274		1,277		1,279		1,281		1,283	1,285
36	1,287	1,289		1,291		1,293		1,295		1,297		1,299		1,302		1,304	1,306
37	1,308	1,310		1,312		1,314		1,316		1,318		1,320		1,322		1,324	1,326
38	1,328	1,330		1,333		1,335		1,337		1,339		1,341		1,343		1,345	1,347
39	1,349	1,351		1,353		1,355		1,357		1,359		1,361		1,363		1,365	1,367
40	1,369	1,371		1,374		1,376		1,378		1,380		1,382		1,384		1,386	1,388
41	1,390	1,392		1,394		1,396		1,398		1,400		1,402		1,404		1,406	1,408
42	1,410	1,412		1,414		1,416		1,418		1,420		1,422		1,424		1,426	1,428
43	1,430	1,432		1,434		1,436		1,438		1,440		1,442		1,444		1,446	1,448
44	1,451	1,453		1,455		1,457		1,459		1,461		1,463		1,465		1,467	1,469
45	1,471	1,473		1,475		1,477		1,479		1,481		1,483		1,485		1,487	1,489
46	1,491	1,493		1,495		1,497		1,499		1,501		1,503		1,505		1,507	1,509
47	1,511	1,513		1,515		1,517		1,519		1,521		1,523		1,525		1,527	1,529

Продолжение таблицы 51

% доля	%, последний десятичный знак
	0		1		2		3		4		5		6		7	8	9
	Значения
48	1,531	1,533		1,535		1,537		1,539		1,541		1,543		1,545		1,547	1,549
49	1,551	1,553		1,555		1,557		1,559		1,561		1,563		1,565		1,567	1,569
50	1,571	1,573		1,575		1,577		1,579		1,581		1,583		1,585		1,587	1,589
51	1,591	1,593		1,595		1,597		1,599		1,601		1,603		1,605		1,607	1,609
52	1,611	1,613		1,615		1,617		1,619		1,621		1,623		1,625		1,627	1,629
53	1,631	1,633		1,635		1,637		1,639		1,641		1,643		1,645		1,647	1,649
54	1,651	1,653		1,655		1,657		1,659		1,661		1,663		1,665		1,667	1,669
55	1,671	1,673		1,675		1,677		1,679		1,681		1,683		1,685		1,687	1,689
56	1,691	1,693		1,695		1,697		1,699		1,701		1,703		1,705		1,707	1,709
57	1,711	1,713		1,715		1,717		1,719		1,721		1,723		1,725		1,727	1,729
58	1,731	1,734		1,736		1,738		1,740		1,742		1,744		1,746		1,748	1,750
59	1,752	1,754		1,756		1,758		1,760		1,762		1,764		1,766		1,768	1,770
60	1,772	1,774		1,776		1,778		1,780		1,782		1,784		1,786		1,789	1,791
61	1,793	1,795		1,797		1,799		1,801		1,803		1,805		1,807		1,809	1,811
62	1,813	1,815		1,817		1,819		1,821		1,823		1,826		1,828		1,830	1,832
63	1,834	1,836		1,838		1,840		1,842		1,844		1,846		1,848		1,850	1,853
64	1,855	1,857		1,859		1,861		1,863		1,865		1,867		1,869		1,871	1,873
65	1,875	1,878		1,880		1,882		1,884		1,886		1,888		1,890		1,892	1,894
66	1,897	1,899		1,901		1,903		1,905		1,907		1,909		1,911		1,913	1,916
67	1,918	1,920		1,922		1,924		1,926		1,928		1,930		1,933		1,935	1,937
68	1,939	1,941		1,943		1,946		1,948		1,950		1,952		1,954		1,956	1,958
69	1,961	1,963		1,965		1,967		1,969		1,971		1,974		1,976		1,978	1,980
70	1,982	1,984		1,987		1,989		1,991		1,993		1,995		1,998		2,000	2,002
71	2,004	2,006		2,009		2,011		2,013		2,015		2,018		2,020		2,022	2,024
72	2,026	2,029		2,031		2,033		2,035		2,038		2,040		2,042		2,044	2,047
73	2,049	2,051		2,053		2,056		2,058		2,060		2,062		2,065		2,067	2,069
74	2,071	2,074		2,076		2,078		2,081		2,083		2,085		2,087		2,090	2,092
75	2,094	2,097		2,099		2,101		2,104		2,106		2,108		2,111		2,113	2,115
76	2,118	2,120		2,122		2,125		2,127		2,129		2,132		2,134		2,136	2,139
77	2,141	2,144		2,146		2,148		2,151		2,153		2,156		2,158		2,160	2,163
78	2,165	2,168		2,170		2,172		2,175		2,177		2,180		2,182		2,185	2,187
79	2,190	2,192		2,194		2,197		2,199		2,202		2,204		2,207		2,209	2,212

Окончание таблицы 51

% доля	%, последний десятичный знак
	0		1		2		3		4		5		6		7	8	9
	Значения
80	2,214	2,217		2,219		2,222		2,224		2,227		2,229		2,231		2,234	2,237
81	2,240	2,242		2,245		2,247		2,250		2,252		2,255		2,258		2,260	2,263
82	2,265	2,268		2,271		2,273		2,276		2,278		2,281		2,284		2,286	2,289
83	2,292	2,294		2,297		2,300		2,302		2,305		2,308		2,310		2,313	2,316
84	2,319	2,321		2,324		2,327		2,330		2,332		2,335		2,338		2,341	2,343
85	2,346	2,349		2,352		2,355		2,357		2,360		2,363		2,366		2,369	2,372
86	2,375	2,377		2,380		2,383		2,386		2,389		2,392		2,395		2,398	2,401
87	2,404	2,407		2,410		2,413		2,416		2,419		2,422		2,425		2,428	2,431
88	2,434	2,437		2,440		2,443		2,447		2,450		2,453		2,456		2,459	2,462
89	2,465	2,469		2,472		2,475		2,478		2,482		2,485		2,488		2,491	2,495
90	2,498	2,501		2,505		2,508		2,512		2,515		2,518		2,522		2,525	2,529
91	2,532	2,536		2,539		2,543		2,546		2,550		2,554		2357		2,561	2,564
92	2,568	2,572		2,575		2,579		2,583		2,587		2,591		2,594		2,598	2,602
93	2,606	2,610		2,614		2,618		2,622		2,626		2,630		2,634		2,638	2,642
94	2,647	2,651		2,655		2,659		2,664		2,668		2,673		2,677		2,681	2,686
95	2,691	2,295		2,700		2,705		2,709		2,714		2,719		2,724		2,729	2,734
96	2,739	2,744		2,749		2,754		2,760		2,765		2,771		2,776		2,782	2,788
97	2,793	2,799		2,805		2,811		2,818		2,824		2,830		2,837		2,844	2,851
98	2,858	2,865		2,872		2,880		2,888		2,896		2,904		2,913		2,922	2,931
99,0	2,941	2,942		2,943		2,944		2,945		2,946		2,948		2,949		2,950	2,951
99,1	2,952	2,953		2,954		2,955		2,956		2,957		2,958		2,959		2,960	2,961
99,2	2,963	2,964		2,965		2,966		2,967		2,968		2,969		2,971		2,972	2,973
99,3	2,974	2,975		2,976		2,978		2,979		2,980		2,981		2,983		2,984	2,985
99,4	2,987	2,988		2,989		2,990		2,992		2,993		2,995		2,996		2,997	2,999
99,5	3,000	3,002		3,003		3,004		3,006		3,007		3,009		3,010		3,012	3,013
99,6	3,015	3,017		3,018		3,020		3,022		3,023		3,025		3,027		3,028	3,030
99,7	3,032	3,034		3,036		3,038		3,040		3,041		3,044		3,046		3,048	3,050
99,8	3,052	3,054		3,057		3,059		3,062		3,064		3,067		3,069		3,072	3,075
99,9	3,078	3,082		3,085		3,089		3,093		3,097		3,101		3,107		3,113	3,122
100,0	3,142

 

                                                       

1.10. Таблица вероятностей Р для биномиального распределения при р = q = 0,5

(из книги: Ермолаев О. Ю. Математическая статистика для психологов. — М., 2002 — С.294-295)

Примечания к таблице:

* В таблице все величины даны без начального нуля и последующей запятой, так что, если в таблице дано число, например 013, - то это число следует читать как 0,013.

** Знаком + в таблице обозначены значения близкие к 1.

Таблица 52

Т2	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
5	031*	188	500	812	969	+**
6	016	109	344	656	891	984	+
7	008	062	226	500	773	938	992	+
8	004	035	145	363	637	855	965	996	+
9	002	020	090	254	500	746	910	980	998	+
10	001	011	055	172	377	623	828	945	989	998	+
11		006	033	113	274	500	726	887	967	994	+
12		003	019	073	194	387	613	806	981	927	997	+
13		002	011	046	133	291	500	709	867	954	989	998	+	+
14		001	006	029	090	212	395	605	788	849	971	994	999	+	+	+
15			004	018	059	151	304	500	696	910	941	982	996	+	+	+
16			002	011	038	105	227	402	598	773	896	962	989	998	+	+
17			001	006	025	072	166	315	500	685	834	928	975	994	999	+
18			001	004	015	048	119	240	407	593	760	881	952	985	996	999
19				002	010	032	084	180	324	500	676	820	916	968	990	998
20				001	006	021	058	132	252	412	588	748	868	942	979	994
21				001	004	013	039	095	192	332	500	668	808	905	961	987
22					002	008	026	067	143	262	416	584	738	857	933	974
23					001	005	017	047	105	202	339	500	661	798	895	953
24					001	003	011	032	076	154	271	419	581	729	846	924
25						002	007	022	054	115	212	345	500	655	788	885

 

 

 Приложение 2. Глоссарий

 

1. Альтернативная гипотеза — это гипотеза о значимости различий. Она обозначается как Н₁. Альтернативная гипотеза — это то, что мы, как правило, хотим доказать; поэтому иногда ее называют экспериментальной гипотезой.

2. Вариационный (статистический) ряд — таблица, первая строка которой содержит в порядке возрастания  значения признака, а вторая — меры возможности их появления (абсолютные частоты, или относительные частоты, или процентные частоты). 

3. Вероятностная зависимость (стохастическая связь) — это такая связь между явлениями или событиями, при которой появление одного из событий изменяет вероятность появления другого события.

4. Вероятность — мера возможности появления признака (число, не превышающее единицу).

5. Гистограмма — график в виде столбиковой диаграммы, который отражает зависимость между значениями признака и мерами возможности их появления.

6. Диаграмма рассеяния — график, представляющий собой множество (совокупность) точек в двумерном пространстве; координатами этих точек являются значения двух признаков. Такой график отражает зависимость между этими двумя признаками.

7. Дискриминантный анализ («классификация с обучением») предсказывает принадлежность объектов (испытуемых) к одному из известных классов (шкала наименований) по измеренным метрическим (дискриминантным) переменным. Дискриминантные переменные должны быть измерены в количественной шкале, зависимая переменная — в шкале наименований.

8. Дисперсия — — это средний квадрат отклонений всех значений признака от среднего арифметического.

9. Дисперсионный анализ — это анализ изменчивости признака под влиянием каких-либо контролируемых переменных факторов. Признаки должны быть измерены в количественной шкале (интервальной или пропорциональной) и иметь нормальное распределение.

10. Доверительная вероятность — вероятность, с которой принимается нулевая гипотеза, или иначе: вероятность того, что нулевая гипотеза является истинной.

11. Зависимые выборки (связанные выборки) — это одна и та же группа людей, у которых были измерены одни и те же признаки в двух (или более) различных ситуациях, например, «до — после», «фон — стресс».

12. Измерение — это приписывание числовых форм объектам или событиям в соответствии с определенными правилами.

13. Квантили — значения признака, которые делят выборку на определенное количество равных частей. Наиболее распространенные квантили — это медиана; квартили Q ₁ , Q ₂ , Q ₃ (делят выборку испытуемых на 4 равные части); децили D ₁ , D ₂ , D ₃ , D ₄ , D ₅ , D ₆ , D ₇ , D ₈ , D ₉ (делят выборку испытуемых на 10 равных частей); процентили Р₁ ……….Р₉₉ (делят выборку испытуемых на 100 равных частей).

14. Кластерный анализ («классификация без обучения»): по измеренным характеристикам у множества объектов (испытуемых) либо по данным об их попарном сходстве (различии) разбивает это множество объектов на группы, в каждой из которых находятся объекты, более похожие друг на друга, чем на объекты других групп.

15. Корреляционное отношение —  является мерой связи для оценки нелинейных взаимозависимостей между признаками, измеренными по интервальной или пропорциональной шкале.

16. Коэффициент асимметрии — As — параметр, характеризующий асимметричность распределения по сравнению с нормальным распределением.

17. Коэффициент вариации или коэффициент вариативности — V — параметр, показывающий соотношение стандартного отклонения и среднего арифметического.

18. Коэффициент контингенции или тетрахорический коэффициент или коэффициент четырехклеточной сопряженности — φ — является мерой связи между признаками, измеренными по дихотомической шкале наименований.

19. Коэффициент линейной корреляции Пирсона — r_xy —является мерой связи для оценки линейных взаимозависимостей между признаками, измеренными по интервальной или пропорциональной шкале.

20. Коэффициент ранговой корреляции Спирмена — ρ=r_s — является мерой связи между признаками, измеренными по шкале порядка или при сочетании шкалы порядка с интервальной или пропорциональной шкалой.

21. Коэффициент эксцесса — Ex — параметр, характеризующий выпуклость распределения по сравнению с нормальным распределением.

22. Критерий вообще — это решающее правило, обусловливающее поведение в ситуации выбора. 

23. Критерий Вилкоксона — T — непараметрический критерий различий, который позволяет оценить различия между двумя зависимыми выборками: направление и выраженность изменений во втором замере по сравнению с первым. Применяется для сравнения признаков, измеренных по шкалам порядка, интервальной или пропорциональной.

24. Критерий Колмогорова-Смирнова — λ — непараметрический критерий, который позволяет оценить различия между двумя распределениями: найти точку, в которой они наиболее сильно различаются. Применяется для сравнения распределений признаков, измеренных по шкалам порядка, интервальной или пропорциональной.

25. Критерий Макнамары — M — непараметрический критерий, который позволяет оценить различия между двумя зависимыми выборками: два замера признака, измеренного по дихотомической шкале наименований и любым другим, если их результаты могут быть сведены к дихотомической шкале.

26. Критерий Манна-Уитни — U — непараметрический критерий различий, который позволяет оценить различия между двумя независимыми выборками: направление и выраженность значений признака. Применяется для сравнения признаков, измеренных по шкалам порядка, интервальной или пропорциональной.

27. Критерий Стьюдента — t — параметрический критерий различий, который позволяет сравнить два любых параметра распределений, полученных в двух выборках. Применяется для сравнения признаков, измеренных по интервальной или пропорциональной шкале при условии нормального распределения признака.

28. Критерий угловое преобразование Фишера — φ^* — непараметрический критерий различий, который позволяет оценить различия между двумя процентными долями в двух независимых выборках. Применяется для сравнения признаков, измеренных по дихотомической шкале наименований и любым другим, если их результаты могут быть сведены к дихотомической шкале.

29. Критерий Фишера — F — параметрический критерий различий, который позволяет сравнить две дисперсии, полученные в двух выборках. Применяется для сравнения признаков, измеренных по интервальной или пропорциональной шкале при условии нормального распределения признака.

30. Критерий хи-квадрат Пирсона — χ² — непараметрический критерий, который позволяет сравнить два распределения признака: согласованность изменений в распределениях. Таким методом оцениваются различия между распределениями, а также взаимосвязь между признаками. Применяется для сравнения признаков, измеренных по шкале наименований, шкалам порядка, интервальной или пропорциональной.

31. Кумулята — график, отражающий зависимость между значениями признака и соответствующими им накопленными частотами. с которой отвергается нулевая гипотеза (истинная) и принимается альтернативная гипотеза (ложная),

32. Медиана — Ме — это значение признака, которое делит выборку испытуемых на две равные части: 50 % испытуемых имеют значения признака меньше медианы, 50 % испытуемых имеют значения признака больше медианы; медиана является частным видом квантилей.

33. Мера связи — числовая величина, отражающая тесноту (силу для всех типов измерений) и направленность (для качественно-количественного и количественного измерения) зависимости между признаками.

34. Многомерное шкалирование выявляет шкалы как критерии, по которым поляризуются объекты при их субъективном попарном сравнении.

35. Множественный регрессионный анализ предсказывает значения метрической «зависимой» переменной по множеству известных значений «независимых» переменных, измеренных у множества объектов (испытуемых). Все переменные должны быть измерены в количественной шкале.

36. Мода — Мо — это значение признака, которое имеет наибольшую частоту.

37. Мощность критерия — его способность критерия правильно отбрасывать ложную гипотезу. Она определяется эмпирическим путем.

38. Независимые выборки (не связанные выборки) — это две выборки, составленные из разных людей, у которых были измерены одни и те же признаки по одним и тем же методикам.

39. Непараметрические критерии — критерии, не включающие в формулу расчета параметры распределения и основанные на оперировании частотами или рангами (например, критерий знаков, критерий Ван-дер-Вардена и др.). Непараметрические критерии применяются для любых шкал и любых распределений признаков.

40. Нулевая гипотеза — это гипотеза об отсутствии зависимости между признаками или отсутствии различий между выборками. Она обозначается как Н₀.

41. Ошибка первого рода (р-уровень) — вероятность, с которой отвергается нулевая гипотеза, являющаяся истинной, и принимается альтернативная гипотеза, являющаяся ложной.

42. Параметрические критерии служат для проверки гипотез о параметрах распределений или для их оценивания, то есть, является ли параметр, полученный на выборке испытуемых, и параметром генеральной совокупности. Параметрические критерии применяются для оценки параметров признаков, измеренных по интервальной и пропорциональной шкале при условии нормального распределения признаков.

43. Параметры распределений — числовые характеристики, отражающие основные тенденции выраженности и изменчивости исследуемых признаков в исследуемой выборке.

44. Полигон частот или многоугольник частот — график в виде прямой ломаной линии, отражающий зависимость между значениями признака и мерами возможности их появления.

45. Распределение — график, отражающий зависимость между значениями признака и мерами возможности их появления (вероятностями или частотами).

46. Регрессия — график в виде линии, которая отражает зависимость между условными средними значениями одной переменной и значениями другой переменной.

47. Репрезентативность выборки — свойство выборочной совокупности, заключающееся в ее способности адекватно представлять основные характеристики генеральной совокупности (воспроизводятся основные свойства генеральной совокупности).

48. Среднее арифметическое значение — 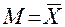 — это то значение признака, которое отражает средний уровень выраженности признака в выборке испытуемых.

49. Стандартное отклонение (или среднеквадратическое отклонение) — 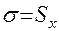 — это среднее отклонение каждого значения признака от среднего арифметического.

50. Статистическая гипотеза — это предположения о свойствах и параметрах генеральной совокупности, различии выборок или зависимости между признаками.

51. Статистический критерий — правило, обеспечивающее надежное поведение, т. е. принятие истинной и отклонение ложной гипотезы с высокой вероятностью. Слова статистический критерий обозначают также метод расчета определенного числа и само это число.

52. Уровень значимо­сти — вероятность ошибочного отклонения нулевой гипотезы.

53. Факторный анализ направлен на выявление структуры переменных как совокупности факторов, каждый из которых — это скрытая, обобщающая причина взаимосвязи группы переменных. Надежные результаты получаются, если переменные измерены в количественной шкале (интервальной или пропорциональной). Число испытуемых должно превышать число переменных (или, по крайней мере, должно быть равно ему).

54. Число степеней свободы  — ν=df — количество возможных направлений изменчивости переменной.

55. Шкала наименований (номинативная, номинальная) является результатом использования при измерении метода регистрации; относится к качественному измерению. 

56. Шкала порядка (порядковая, ординальная) является результатом использования при измерении метода упорядочивания; относится к качественно-количественному измерению.

57. Шкала равных интервалов (интервальная) является результатом измерения методом соотнесения (с эталонной единицей измерения), нулевая точка шкалы произвольна и не указывает на отсутствие измеряемого свойства; является метрической шкалой и относится к количественному измерению.

58. Шкала равных отношений (пропорциональная) является результатом измерения методом соотнесения (с эталонной единицей измерения), существует абсолютный нуль, который означает отсутствие измеряемого свойства; является метрической шкалой и относится к количественному измерению.

 

Приложение 3. Ответы на задачи для самоконтроля усвоения знаний

 

Тема 4. Практическое задание № 1

xi	134 42	125 29	126 33	124 27	126 34	121 22	109 8	125 30	143 49	106 6	134 43	103 5	128 37	∑
Ri	42,5	30,5	33,5	27,5	33,5	23	8	30,5	49	6	42,5	4,5	37	368
xi	131 40	141 48	127 35	125 31	103 4	117 16	107 7	133 41	111 9	127 36	122 25	147 50	125 32
Ri	40	48	35,5	30,5	4,5	16,5	7	41	10	35,5	25,5	50	30,5	374,5
xi	140 47	137 45	118 18	114 13	120 19	121 23	122 26	121 24	111 10	135 44	129 38	116 14	124 28
Ri	47	45	18	13	20	23	25,5	23	10	44	38,5	14,5	27,5	349
xi	120 20	93 1	100 2	117 17	129 39	112 12	111 11	116 15	120 21	102 3	139 46
Ri	20	1	2	16,5	38,5	12	10	14,5	20	3	46			183,5

                    

Расчетная сумма рангов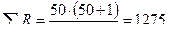

Реальная сумма проставленных рангов ∑R=368+374,5+349+183,5=1275

Тема 4. Практическое задание № 2

φ_расч. = – 0,508 χ²_расч. = 3,096

Оценку значимости расчетного значения коэффициента контенгенции производим с помощью критерия хи-квадрат Пирсона.

χ²_табл. = 3,84 для р = 0,95  

χ²_расч=3,0,96 < χ²_табл=3,84     

Следовательно, статистически значимой взаимосвязи между признаками нет, то есть семейное положение студентов не влияет на их отчисление из ВУЗа.                                                                                                                                                                   

Тема 4. Практическое задание № 3

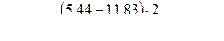
Оценку значимости рангово-бисериального коэффициента корреляции производим с помощью критерия Стьюдента.

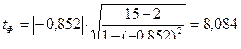
t _Ф =8,084 ≥ t _табл.= 3,01 при р= 0,99 Следовательно, между признаками существует статистическая значимая связь, то есть существует взаимосвязь между полом и развитием вервальных способностей.

Тема 4. Практическое задание № 4

Для а=2 Т_а= (2³–2)/12=1,5

Для а=3 Т_а= (3³–3)/12=2,0

Для а=4 Т_а= (4³–4)/12=5,0

Для а=5      Т_а= (5³–5)/12=10,0

 

Для а=6 Т_а= (6³–6)/12=17,5

 

Тема 4. Практическое задание № 5

 

С поправкой на связанные ранги

 

 

ρ_расч.=|–0,703| > ρ_расч.= 0,64 при р=0,95 Следовательно, корреляция достоверно отличается от 0, т.е. взаимосвязь между выраженностью акцентуируемых у матери и сына существует и она обратно пропорциональная.

 

 

 

           

Приложение 4. Англо-русский словарь статистических терминов

Словарь позаимствован из пособия, написанного А. Д. Наследовым.

           

Этот словарь может быть полезен при работе с компьютерными пакетами математико-статистического анализа (SРSS или STATISTICA).

1- Sample K-S Test —	критерий (тест) Колмо­горова-Смирнова
1-tailed —	односторонний (направленный) уровень значимости
2-tailed —	двусторонний (ненаправленный) уровень значимости
Absolute value —	абсолютное значение
Actual (value, group) —	действительное, реаль­ное (значение, группа)
Add —	добавить
Adjusted —	исправленный (улучшенный)
Advanced (Model) —	специальная, более совер­шенная (модель)
Agglomeration schedule —	последовательность агломерации (объединения)
ALSCAL —	программа неметрического мно­гомерного шкалирования
Amalgamation —	слияние, объединение
Analyze —	анализировать
ANOVA —	дисперсионный анализ
Approach —	подход
Assume —	принятие (допущение, предположение)
Asymmetric —	асимметричная
Asymp. Sig. —	примерный (приближенный) уровень значимости
Average Linkage —	средней связи (метод клас­теризации)
Averaged —	усредненный
Axis —	ось (координат)
Bartlett 's Test of Sphericity —	тест сферичнос­ти Бартлета
Based on —	основанный на (исходящий из)
Beta-Coefficient —	стандартизированный ко­эффициент регрессии
Between (objects, variables) —	между (объекта­ми, переменными)
Between Groups Linkage —	межгрупповой (средней) связи (метод кластеризации)
Between-Group —	межгрупповой
Between-Subject —	между объектами (межгруп­повой)
Binary Measures —	количественные показате­ли (меры) для бинарных данных
Binomial Test —	биномиальный критерий
Bivariate —	двумерный
Box's M - test —	М-тест Бокса
Canonical Analysis —	канонический анализ
Case —	случай (испытуемый)
Casewise deletion —	исключение из анализа случая (строки), в котором имеется про­пуск хотя бы одного значения
Categories —	категории (номинативного при­знака)
Categorization —	операция выделения интер­валов квантования (или значений пере­менной) при построении гистограммы и составлении таблицы частот
Cell —	ячейка (таблицы)
Central Tendency —	центральная тенденция (мера)
Centroid —	центроид
Chi I —	хи-квадрат
Chi-square (Test) —	хи-квадрат (критерий)
Classify —	классифицировать
Cluster Combined —	объединенные кластеры
Cluster Method —	метод кластеризации
Coefficient ( s ) —	коэффициент(ы)
Column —	столбец
Combine —	объединение, объединять
Communality —	общность
Compare —	сравнивать
Compare Means —	сравнение средних
Comparison —	сравнение
Complete Linkage —	полной связи (метод кла­стеризации)
Compute —	вычисление, вычислять
Conditionality —	условность, обусловленность (подгонки)
Confidence (Interval) —	доверительный (ин­тервал)
Constant —	константа
Contrast —	контраст
Controlling for... —	контролировать (фиксиро­вать) для...
Convergence —	сходимость (при подгонки)
Corrected (Model) —	исправленная, скоррек­тированная (модель)
Correlate —	коррелировать (определять совме­стную изменчивость)
Correlation matrix —	корреляционная матрица
Count Measure —	количественный показатель (мера) частоты
Covariance —	ковариация
Covariate —	ковариата
Criteria (Criterion) —	условие (критерий)
Crosstabulation (Crosstab) —	сопряженность, кросстабуляция
Cumulative frequencies —	— кумулятивные (накоп­ленные) частоты
Custom Model —	специальная модель
Cut Point —	точка деления
Data —	данные
Data Editor —	редактор (таблица) исходных данных в SPSS
Data Reduction —	сокращение данных (метод)
Define (Groups) —	определение, задание (групп)
Degrees of freedom (df) —	число степеней сво­боды
Deletion —	удаление (исключение)
Dendrogram —	дендрограмма (древовидный график)
Density Function —	функция плотности веро­ятности
Dependent Sample —	зависимая выборка
Dependent-Samples T Test —	критерий t-Стьюдента для зависимых выборок
Derived —	производный
Descriptive Statistics —	описательные статис­тики
df —	число степеней свободы (сокр.)
Difference —	разность, различие
Dimension —	шкала
Discriminant Analysis —	дискриминантный анализ
Dispersion —	изменчивость
Dissimilarity —	различие
Distance —	расстояние
Distribution —	распределение
Distribution Function —	функция распределе­ния (вероятности)
Effect —	влияние (фактора)
Eigenvalue —	собственное значение
Enter —	исходный (метод)
Entry —	включение
Epsilon Corrected —	с Эпсилон-коррекцией
Equal —	одинаковые
Equal Variances —	одинаковые (эквивалент­ные) дисперсии
Equality (of Variances) —	эквивалентность, ра­венство (дисперсии) ошибка
Error —	оценка
Estimate —	Евклидово расстояние
Euclidean Distance —	точный, точно
Exact —	точный уровень значимости
Exact Sig. —	исключение (объектов)
Exclude (cases) —	ожидаемая (тео­ретическая) частота (значение)
Expected Frequency (Value) —	«объясненная» (дис­персия)
Explained (Variance) —	метод факторизации (эк­стракции факторов)
Extraction Method —	фактор
Factor —	факторный анализ
Factor Analysis —	факторные нагрузки
Factor Loadings —	коэффициенты фак­торных оценок
Factor Score coefficients —	факторные оценки
Factor Scores —	точный критерий Фишера
Fisher's Exact Test —	постоянный, фиксированный (фактор)
Fixed (Factor) —	для всей матрицы
For Matrix —	значение Р-критерия (Р-отношения) для дисперсий
F-ratio Variances —	частота
Frequency —	таблицы частот
Frequency tables —	критерий Фридмана
Friedman test (ANOVA) —	модель, включающая все факторы
Full factorial model —	дальнего соседа (метод кластеризации)
Furthest Neighbor —	общая линейная модель
General Linear Model —	обобщенный метод
Generalized least squares —	наименьших квадратов
GLM —	общая линейная модель (сокр.)
Goodness-of-fit —	качество подгонки
Group Membership —	принадлежность к группе
Group Plots —	график(и) для всей группы
Grouping Variable —	группирующая перемен­ная
Han Hierarchical Cluster Analysis —	иерархический кластерный анализ
Histogram —	гистограмма
Homogeneity of Variances —	гомогенность (од­нородность) дисперсий горизонтальная (ориентация)
Horizontal —	факторный анализ образов
Image Factoring —	улучшение (с поправкой)
Improvement —	включение
Independent Sample —	независимая выборка
Independent-Samples T Test —	критерий t-Стьюдента для независимых выборок
Individual Differences (model) —	индивидуальных различий (модель)
INDSCALE —	программа многомерного шкалирования индивидуальных различий
Initial (conditions) —	начальные (условия)
Input File —	исходный, входящий файл
Interaction —	взаимодействие
Intercept —	свободный член (уравнения)
Interval —	интервальная (шкала)
Interval data —	данные в интервальной шкале
Interval Scale —	интервальная шкала
Inverse distribution function —	обратная функция распределения итерация
Iteration —	итерация
Iteration history —	«история» (последовательность) итераций
Iterations stopped... —	итерации остановлены...
Joining —	объединение, связь
Kendall 's tau —	тау-Кендалла (корреляция)
Kendall 's tau-b —	тау-b Кендалла (корреляция)
Kruskal-Wallis H —	критерий Н-Краскала Уоллеса
Kruskal-Wallis one-way analysis of variance —	однофакторный дисперсионный анализ Краскала-Уоллеса
Kurtosis —	эксцесс
Label —	метка, обозначение
Level —	уровень
Level of Measurement —	уровень (шкала) измерения
Levene's Test —	критерий Ливена
Linear Regression —	линейный регрессионный
Linkage —	соединение, связь
List —	список
Listwise —	построчно
Listwise Deletion —	исключение из анализа случая (строки), в котором имеется пропуск хотя бы одного значения
Loading —	нагрузка
Mann-Whitney U —	критерий U-Манна-Уитни
MANOVA —	многомерный дисперсионный анализ
Marginal (Means) —	отдельные (средние значения)
Matrices —	матрицы
Matrix —	матрица
Mauchly's Test of Sphericity —	тест сферично сти
MoynjiM Maximum Likelihood —	максимального правдоподобия (метод)
McNemar Test —	критерий Мак-Нимара
Mean —	среднее
Mean of Squares (MS) —	средний квадрат
Mean Substitution —	замена пропущенных зна­чений средними
Means Plot —	график средних значений
Measurement —	измерение
Median —	медиана
Missing (Values) —	пропущенные (значения)
M-L (Maximum likelihood) —	максимального правдоподобия (метод, оценка)
Mode —	мода
Monte Carlo Method —	статистический метод «Монте-Карло»
Multidimensional Scaling —	многомерное шка­лирование
Multiple —	множественный
Multiple comparisons —	множественные срав­нения (средних)
Multivariate —	многомерный
Multivariate Approach —	многомерный подход
Nearest Neighbor —	ближайшего соседа (метод кластеризации)
Negative —	отрицательный
Next —	следующий
Nominal—	номинальная (шкала)
Nonparametric Test —	непараметрический кри­терий
Normal Curve —	нормальная кривая
Number —	количество (численность), номер
Observed Frequency —	наблюдаемая (эмпири­ческая) частота
Observed Prop. —	наблюдаемое (эмпиричес­кое) соотношение
One-Sample Kolmogorov-SmirnovTest —	крите­рий (тест) Колмогорова-Смирнова
One-Sample T Test —	критерий t-Стьюдента для одной выборки
One-tailed (one-sided) —	односторонний кри­терий (для проверки односторонних гипо­тез); one-tailed — дословно однохвостый
One-Way ANOVA —	однофакторный дисперси­онный анализ
Ordinal (Rank order) —	порядковая (ранговая) (шкала)
Paired-Samples T Test —	критерий t-Стьюдента для зависимых выборок
Pairwise —	попарно, попарный
Partial Correlation —	частная корреляция (ко­эффициент)
Pearson Chi-Square —	критерий хи-квадрат Пирсона
Pearson correlation —	корреляция Пирсона
Pearson r —	корреляция Пирсона
Percentage —	процент
Percentiles —	процентили
Mean of Squares (MS) —	фи-коэффициент сопряженности
Phi 4-points correlation —	(четырехклеточный) фи—коэффициент сопряженности (Пир­сона)
Pillai's Trace —	след Пиллая
P-Ievel —	статистическая значимость (р-уровень)
Plot —	диаграмма
Polynomial —	полином (многочлен)
Post Hoc —	апостериорный (после подтверж­дения гипотезы)
P-P Plot —	график накопленных частот
Predicted (value, group) —	предсказанное (зна­чение, группа)
Principal Axis Factoring —	факторный анализ методом главных осей
Principal Components —	главных компонент (анализ)
Prior probabilities —	априорные вероятности
Probability —	вероятность
Probability of group membership —Proximity —	вероятность принадлежности к группе
Proximality —	близость
PROXSCAL —	программа неметрического многомерного шкалирования
Q-Q Plot —	квантильный график
Quantile —	квантиль
Quartile —	квартиль
R Square (R2) —	коэффициент детерминации (квадрат коэффициента корреляции)
Random (Factor) —	случайный (фактор)
Range —	размах
Rank —	ранг
Rank (Cases) —	ранжировать (объекты)
Ratio —	абсолютная шкала (равных отно­шений)
Raw —	строка
Raw Data —	данные в строках (типа «объект-признак»)
Rectangular (matrix)—	прямоугольная (матрица)
Regression —	регрессионный
Regression Coefficient —	коэффициент рег­рессии
Regression Line —	линия регрессии
Related Samples —	зависимые (связанные) вы­борки
Removal —	удаление
Repeated Measures —	повторные измерения
Repeated Measures ANOVA —	дисперсионный анализ с повторными измерениями
Residual —	остаток, отклонение (ошибка мо­дели)
Residual analysis —	анализ остатков (ошибок)
Rotation (Factors) —	вращение (факторов)
Rotation Method —	метод вращения
Row —	строка
RSQ (R-square) —	квадрат коэффициента кор­реляции, коэффициент дискриминации (г-квадрат)
Run —	серия
Runs Test —	критерий серий
Sample —	выборка
Scaling model —	модель шкалирования
Scatter Plot —	диаграмма рассеивания
Scheffé test —	метод Шеффе (множественных сравнений средних)
Scree plot —	график собственных значений
Scree-test —	критерий отсеивания
Scrollsheet —	таблица результатов статистичес­кого анализа
Separate (Line) —	отдельная (линия)
Set —	множество
Shape —	уточнить
Sig. —	уровень значимости (р-уровень)
Sign —	знак
Sign Test —	критерий знаков
Significance Level —	уровень статистической значимости (р-уровень)
Significant —	статистически значимый
Similarity —	сходство
Simple —	простой
Simple Matching —	простой коэффициент совстречаемости (бинарный)
Single Linkage —	одиночной связи (метод кла­стеризации)
Size difference —	величина различий (би­нарная)
Skewness —	асимметрия
Slope —	уклон, наклон (прямой по отноше­нию к оси X), значение коэффициента регрессии
Solution —	решение (выбор)
Source —	источник (изменчивости, влияния)
Spearman's rho (r) —	корреляция Спирмена (коэффициент)
Specify —	определять
Spreadsheet —	электронная таблица для исход­ных данных
SPSS —	компьютерная программа «Статисти­ческий пакет для социальных наук» (сокр.)
Square asymmetric (symmetric) matrix —	квад­ратная асимметричная (симметричная) матрица
Squared (Euclidean distance) —	квадрат (Евкли­дова расстояния)
S-stress convergence —	величина сходимости 8-стресса
Stage —	ступень (этап, шаг)
Standard deviation —	стандартное отклонение (сигма)
Standard error —	стандартная ошибка
Standardized (Beta-) Coefficients —	стандарти­зированные (бета-) коэффициенты рег­рессии
STATISTICA —	компьютерная программа для статистического анализа данных
Statistical Test —	статистический критерий (тест)
Std. Deviation —	стандартное отклонение (сигма)
Std. Error —	стандартная ошибка
Step —	шаг
Stepwise Method —	пошаговый метод
Stimulus —	стимулы
Stress —	стресс, в многомерном шкалировании
Stub-and-Banner Tables —	таблицы сопряжен­ности для двух и более признаков
Subject —	субъект
Subject Weight —	индивидуальный вес
Subset —	подмножество
Sum —	сумма
Sum of Squares (SS) —	сумма квадратов
Summary —	итог
Suppress —	скрыть
Symmetric —	симметричная
Syntax —	командный файл в SPSS
Table —	таблица
Test —	статистический критерий
Test Prop. —	ожидаемое (теоретическое) соот­ношение
Test Statistics —	результаты статистической проверки
Test Value —	заданное (тестовое) значение
Tied Ranks —	связанные (повторяющиеся) ранги
Ties (of ranks) —	связи, повторы (рангов)
Total —	итог (сумма)
Transform (Values, Measures) —	преобразование (значений, мер)
Tree Diagram —	древовидная диаграмма
Two-tailed (two-sided) —	двусторонний крите­рий (для проверки двусторонних гипотез)
Univariate (procedure, approach) —	одномерный (метод, подход)
Unrotated —	до вращения
Unstandardized Coefficient —	коэффициент рег­рессии (не стандартизированный)
Untie tied observation —	разъединять (разли­чать) связанные (одинаковые) данные
Unweighted least squares —	метод не взвешен­ных наименьших квадратов
Valid n —	число случаев, по которому были проведены расчеты
Value —	значение
Var —	переменная (сокр.)
Variable —	переменная (признак)
Variable List —	список переменный
Variance —	дисперсия
Varimax	метод варимакс (вращения факто­ров)
Vertical —	вертикальная (ориентация)
Weight —	вес
Wilcoxon Signed-rank (Matched pairs) test —	критерий Т-Вилкоксона
Wilcoxon test —	критерий Вилкоксона
Wilks' Lambda —	лямбда Вилкса
Within —	внутри
Within-Group —	внутригрупповой
Within-Subject —	внутри объектов (внутригрупповой)
XI —	хи-квадрат критерий
Yates' corrected —	с поправкой Йетса
Yule's Q —	Юла Q-коэффициент
Z-score —	z-значение

 

 

[1] Аддитивность — (от лат. additivus – прибавляемый; матем.: свойство по значению; прил. - аддитивный) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, при любом разбиении объекта на части. Следовательно, можно утверждать, что для данных показателей соблюдается правило аддитивности: уровень характеристики целого складывается из значений данной характеристики отдельных компонентов с учетом их доли в составе целого (http://ru.wiktionary.org/wiki/аддитивность).

 

[2] Единицей измерения в стандартизованных шкалах является стандартное отклонение, полученное на выборке стандартизации.

[3] Полный набор событий.

[4] Закон Лапласа-Гаусса (по имени ученых, независимо открывших и исследовавших его) из-за широкого распространения в природе первоначально принимался за норму распределения любой случайной величины. Этим и обусловлено название "нормальный" закон.

[5] Знак расчетной меры взаимосвязи интерпретируется только для зависимостей между признаками, измеренными по шкале порядка, интервальной или пропорциональной шкале. Для взаимосвязей признаков, измеренных по шкале наименований, знак не интерпретируется, так как он зависит от расположения градаций (значений) признака, которые в данной шкале не могут быть упорядочены, так как в ней не применяется операция сравнения «больше — меньше».

[6] Терентьев П. В. Метод корреляционных плеяд // Вестник ЛГУ, 1959, №9. Он же. Дальнейшее развитие метода корреляционных плеяд // Применение математических методов в биологии. ЛГУ, 1960.

[7] Olson D., Miller R. Morphological Integration. – N.Y., 1958 ( Ch. 1, 4, 5, 7).

[8] Докторов Б.З. Сравнение рабочих характеристик различных методов факторного анализа при комплексном изучении человека // Человек и общество, XII, 1972.

[9] Данный алгоритм разработан В. А. Тютюнником на основе анализа работ П. В. Терентьева.

[10] Суходольский Г. В. Основы математической статистики для психологов. — СПб., 1972 — Стр. 279.

 

[11] При сравнении эмпирического и теоретического распределений вместо частот второго эмпирического распределения следует ввести в таблицу частоты теоретического распределения.